Trouvez l'aire d'un cercle de rayon \( a \) en utilisant intégrales dans l'analyse mathematique.
Problème: Trouver l'aire d'un cercle de rayon \( a \).
Solution au problème :
L'équation du cercle ci-dessus est donnée par
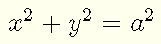
Le cercle est symétrique par rapport aux axes x et y, on peut donc trouver l'aire d'un quart de cercle et multiplier par 4 pour obtenir l'aire totale du cercle.
Résolvez l'équation ci-dessus pour \( y \)
L'équation du demi-cercle supérieur (y positif) est donnée par
\( y = \sqrt { a^2 - x^2 } \)
Factoriser \( a^2 \) à l'intérieur du radicande
\( y = \sqrt { a^2(1 - x^2/a^2) } \)
Prenez \( a^2 \) sous le radicande et réécrivez \( y \) comme suit
\( y = a \sqrt { 1 - x^2 / a^2 } \)
Nous utilisons des intégrales pour trouver l'aire du quart supérieur droit du cercle comme suit
(1/4) Aire du cercle = \( \displaystyle \int_0^a a \sqrt{1-x^2/a^2} dx \)
Remplaçons \( \; x / a \) par \( \; \sin t \) de sorte que \( \sin t = x / a \) et \( dx = a \cos t \; dt \; \) et l'aire est donnée par
(1 / 4) Aire du cercle = \( \displaystyle \int_0^{\pi/2} a^2 \sqrt{1-\sin^2t} \cos t \; dt\)
Nous utilisons maintenant l'identité trigonométrique
\( \sin^2 t + \cos^2 t = 1 \)
qui donne
\( \sqrt{1-\sin^2t} = \cos t \quad \) puisque t varie de 0 à \( \pi/2 \) donc
(1 / 4) Aire du cercle = \( \displaystyle \int_0^{\pi/2} a^2 \cos^2t \; dt\)
Utilisez l'identité trigonométrique \( \; \cos^2 t = ( \cos 2t + 1 ) / 2 \;\) pour linéariser l'intégrande;
(1 / 4) Aire du cercle = \( \displaystyle \int_0^{\pi/2} a^2 ( \cos 2t + 1 ) / 2 \; dt\)
Évaluer l'intégrale
(1/4) Aire du cercle = \( \displaystyle (1/2)a^2 \left[(1/2) \sin 2t + t\right]_0^{\pi/2} \)
Simplifier
(1 / 4) Aire du cercle = \( (1/4) \pi a^2 \)
L'aire totale du cercle s'obtient en multipliant par 4
Aire du cercle = \( 4 \times (1/4) \pi a^2 = \pi a^2 \)
