| La fonction trigonométrique sinus
f (x) = a * sin (bx + c) + d
, son amplitude, sa période et son déphasage sont explorés de manière interactive à l'aide d'une applet. L'enquête est réalisée en modifiant les paramètres a, b, c et d. Pour comprendre en profondeur les effets de chaque paramètre sur le graphe de la fonction, on change un paramètre à la fois au début. Puis, plus tard on peut modifier plusieurs paramètres.
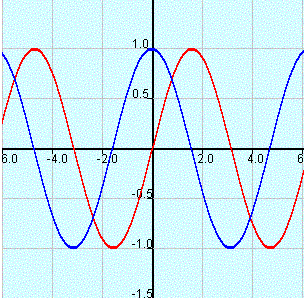
Exploration et compréhension du déphasage se fait en comparant le décalage entre les graphes des deux fonctions:
f (x) = a * sin (bx + c) + d en bleu et
g (x) = a * sin (bx) + d
en rouge comme le montre la figure ci-dessous.
Vous pouvez aussi envisager un autre tutoriel sur le cercle unité trigonométriques .
Une fois que vous avez terminé le didacticiel présente, vous voudrez peut-être au travail grâce à un auto-test sur les graphiques trigonométriques .
Interactive Applet Java Tutorial Utilisation
Comment les 4 coefficients a, b, c et d affecter le graphe de f (x)?
Amplitude
- utiliser la barre de défilement pour mettre a = 1, b = 1, c = 0 et d = 0. Notez f (x) et prendre note de l'amplitude, la période et le déphasage de f (x)? Aujourd'hui, le changement a, comment est-elle une incidence sur le graphique? L'amplitude est définie comme étant | a |.
Réponse Période - A = 1, c = 0, d = 0 et le changement b. Trouver la période à partir du graphique et la comparer à 2Pi / | b |. Comment ne b affectent le graphe de f (x)? La période est la distance horizontale (le long de l'axe des x) entre deux points: l'un est le point de départ d'un cycle et le second est le point final du cycle de même.
Réponse Phase Shift - A = 1, b = 1, d = 0 et c le changement à partir de zéro va lentement vers les valeurs positives plus grandes. Prenez note de l'évolution, est-il à gauche ou à droite?
Réponse - A = 1, b = 1, d = 0 et c le changement à partir de zéro va lentement pour des valeurs négatives plus petits. Prenez note de l'évolution, est-il à gauche ou à droite?
Réponse - Répétez l'opération pour b = 2,3 et 4, de mesurer l'évolution et la comparer à-c / b (le décalage de phase).
Réponse Vertical Shift - la série A, B et C non nul changements de valeurs et d. Quel est le sens du déplacement de la courbe?
Réponse
Plus de références et des liens sur les fonctions sinus.
|
