Gaussian functions of the form
\[ f(x) = a e^{-\frac{(x-b)^2}{c^2}} \]and the properties of their graphs are explored.
Properties of the Graphs of Gaussian Functions
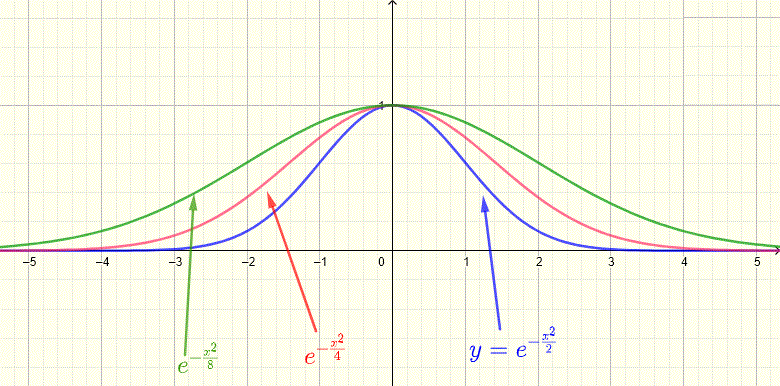
Below are shown Gaussian functions with \( a = 1 \), \( b = 0 \), and different values of \( c \). Note that all functions of the form \( f(x) = e^{-\frac{x^2}{c^2}} \) have a maximum equal to \( 1 \) at \( x = 0 \). We also conclude that the parameter \( c \) controls the width of the graph of \( f \). As \( c \) gets larger, the width of the graph gets larger.
Below are shown Gaussian functions with \( a = 1 \), \( c^2 = 2 \), and different values of \( b \). We also conclude that the parameter \( b \) controls the horizontal position (or shifting) of the graph. When \( b \) is positive, the graph is shifted to the right, and when \( b \) is negative, the graph is shifted to the left.
Gaussian Function as a Probability Density Function
The probability density function of a random variable that is normally distributed with mean \( \mu \) and variance \( \sigma^2 \) is given by a Gaussian of the form:
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma} \right)^2} \]and
\[ \int_{-\infty}^{+\infty} \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma} \right)^2} dx = 1 \]Interactive Tutorial to Further Explore Gaussian Functions
Change parameters \( a \), \( b \), and \( c \) in the function
\[ f(x) = a e^{-\frac{(x-b)^2}{c^2}} \]following the activities below and explain.
Tutorial Questions and Answers
- Click on the button above "draw" to start. The graph of the Gaussian function is displayed.
- Use the sliders to set parameter \(b\) to 0 and \(c\) to 1 and change parameter \(a\). What happens to the graph?
- Now set parameter \(a\) to 1 and \(c\) to 1 and change parameter \(b\). What happens to the graph? Explain analytically.
- Set parameters \(a\) to 1 and \(b\) to 0 and change parameter \(c\). What happens to the graph when \(c\) takes small values? What happens to the graph when \(c\) takes larger values?
Answer
The graph expands vertically as \(a\) increases. The y-values of the points making the graph are multiplied by the value of \(a\).
Answer
As \(b\) increases, the graph is shifted to the right. As \(b\) decreases, the graph is shifted to the left.
Answer
As \(c\) is made small, the graph shrinks horizontally. As \(c\) is made large, the graph expands horizontally.