
Wie löst man trigonometrische Gleichungen? Es werden Fragen zusammen mit detaillierten Lösungen und Erklärungen präsentiert.
Finden Sie alle Lösungen der trigonometrischen Gleichung \[ \sqrt{3} \sec(\theta) + 2 = 0\]
Unter Verwendung der Identität \(\sec(\theta) = \dfrac{1}{\cos(\theta)}\) schreiben wir die Gleichung in der Form um:
\[ \cos(\theta) = -\dfrac{\sqrt{3}}{2} \]Finden Sie den Referenzwinkel \(\theta_r\), indem Sie die obige Gleichung ohne das Minuszeichen lösen:
\[ \cos(\theta_r) = \dfrac{\sqrt{3}}{2} \]wobei \(\theta_r\) spitz ist und gleich dem Referenzwinkel ist. Die Lösung der Gleichung \( \cos(\theta_r) = \dfrac{\sqrt{3}}{2} \) ist gegeben durch:
\[ \theta_r = \dfrac{\pi}{6} \]Verwenden Sie den Referenzwinkel \(\theta_r\), um die Lösungen \(\theta_1\) und \(\theta_2\) im Intervall \([0 , 2\pi)\) der gegebenen Gleichung zu bestimmen. Die Gleichung \(\cos(\theta) = -\dfrac{\sqrt{3}}{2}\) deutet darauf hin, dass \(\cos(\theta)\) negativ ist, und das bedeutet, dass die Endseite des Winkels \(\theta\), der die gegebene Gleichung löst, entweder im Quadranten II oder III liegt, wie unten mit dem Einheitskreis dargestellt.

Daher die Lösungen im Intervall\( [0 , 2 \pi) \):
\[ \theta_1 = \pi - \theta_r = \pi - \dfrac{\pi}{6} = \dfrac{5\pi}{6}\] \[ \theta_2 = \pi + \theta_r = \pi + \dfrac{\pi}{6} = \dfrac{7\pi}{6}\]Verwenden Sie die Lösungen im Intervall [0 , 2 \pi), um alle Lösungen durch Hinzufügen von Vielfachen von \( 2 \pi \) wie folgt zu finden:
\[ \theta_1 = \dfrac{5\pi}{6} + 2n\pi ,\quad n = 0, \pm 1 , \pm 2, \ldots\] \[ \theta_2 = \dfrac{7\pi}{6} + 2n\pi ,\quad n = 0, \pm 1 , \pm 2, \ldots\]Unten sind die grafischen Lösungen im Intervall \( [0 , 2 \pi) \) dargestellt.

Lösen Sie die trigonometrische Gleichung \[ 2 \sin(\theta) = -1 \]
Schreiben Sie die obige Gleichung in einfacher Form um, wie unten gezeigt.
\[\sin(\theta) = -\dfrac{1}{2}\]Finden Sie den Referenzwinkel \(\theta_r\), indem Sie die Gleichung ohne das Minuszeichen lösen:
\[ \sin(\theta_r) = \dfrac{1}{2}\]\( \theta_r\) ist spitz und gleich:
\[\theta_r = \dfrac{\pi}{6}\]Verwenden Sie den Referenzwinkel \(\theta_r\), um die Lösungen \(\theta_1\) und \(\theta_2\) im Intervall \([0 , 2\pi)\) der gegebenen Gleichung zu bestimmen. Die Gleichung \(\sin(\theta) = -\dfrac{1}{2}\) deutet darauf hin, dass \(\sin(\theta)\) negativ ist, und das bedeutet, dass die Endseite des Winkels \(\theta\) entweder im Quadranten III oder IV liegt, wie im Einheitskreis unten gezeigt.
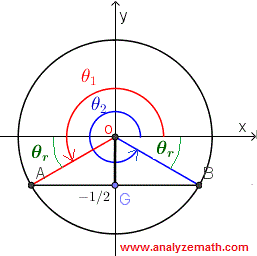
Daher die Lösungen:
\[\theta_1 = \pi + \theta_r = \pi + \dfrac{\pi}{6} = \dfrac{7\pi}{6}\] \[ \theta_2 = 2\pi - \theta_r = 2\pi - \dfrac{\pi}{6} = \dfrac{11\pi}{6}\]Verwenden Sie die Lösungen im Intervall \([0 , 2\pi)\), um alle Lösungen durch Hinzufügen von Vielfachen von \(2\pi\) wie folgt zu finden:
\[\theta_1 = \dfrac{7\pi}{6} + 2n\pi , \quad n = 0, \pm 1 , \pm 2, \ldots\] \[\theta_2 = \dfrac{11\pi}{6} + 2n\pi , \quad n = 0, \pm 1 , \pm 2, \ldots\]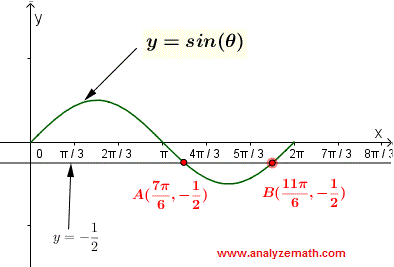
Lösen Sie die trigonometrische Gleichung \[ \sqrt{2} \cos\left(3x + \dfrac{\pi}{4}\right) = -1 \]
Sei \( \theta = 3x + \dfrac{\pi}{4} \) und schreiben Sie die Gleichung in einfacher Form um.
\[ \sqrt{2} \cos(\theta) = -1 \] \[ \cos(\theta) = -\dfrac{1}{\sqrt{2}} \]Finden Sie den Referenzwinkel \( \theta_r \), indem Sie \( \cos(\theta_r) = \dfrac{1}{\sqrt{2}} \) für den spitzen Winkel \( \theta_r \) lösen.
\[ \theta_r = \dfrac{\pi}{4} \]Verwenden Sie den Referenzwinkel \(\theta_r\), um die Lösungen \(\theta_1\) und \(\theta_2\) im Intervall \([0 , 2\pi)\) der gegebenen Gleichung zu bestimmen.
Die Gleichung \( \cos(\theta) = - \dfrac{1}{\sqrt{2}}\) deutet darauf hin, dass \(\cos(\theta)\) negativ ist, und das bedeutet, dass die Endseite des Winkels \(\theta\) entweder im Quadranten II oder III liegt. Daher sind die beiden Lösungen der Gleichung \(\cos(\theta) = - \dfrac{1}{\sqrt{2}}\) im Intervall \([0 , 2\pi)\) gegeben durch:
\[ \theta_1 = \pi - \theta_r = \pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4}\] \[ \theta_2 = \pi + \theta_r = \pi + \dfrac{\pi}{4} = \dfrac{5\pi}{4}\]Wir schreiben nun die allgemeinen Lösungen, indem wir Vielfache von \( 2\pi \) wie folgt hinzufügen:
\[ \theta_1 = \dfrac{3\pi}{4} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \] \[ \theta_2 = \dfrac{5\pi}{4} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \]Wir ersetzen nun \( \theta_1 \) und \( \theta_2 \) durch den Ausdruck \( 3x + \dfrac{\pi}{4} \):
\[ 3x + \dfrac{\pi}{4} = \dfrac{3\pi}{4} + 2n\pi \] \[ 3x + \dfrac{\pi}{4} = \dfrac{5\pi}{4} + 2n\pi \]und lösen nach \( x \) auf, um die Lösungen für \( x \) zu erhalten.
\[ x_1 = \dfrac{\pi}{6} + \dfrac{2n\pi}{3}, \quad n = 0, \pm 1, \pm 2, \ldots \] \[ x_2 = \dfrac{\pi}{3} + \dfrac{2n\pi}{3}, \quad n = 0, \pm 1, \pm 2, \ldots \]Lösen Sie die trigonometrische Gleichung \[ - 2 \sin^2 x - \cos x = - 1 \]
Die obige Gleichung kann faktorisiert werden, wenn alle darin enthaltenen trigonometrischen Funktionen gleich sind. Unter Verwendung der Identität \( \sin^2 x = 1 - \cos^2 x \) können wir die obige Gleichung unter Verwendung derselben trigonometrischen Funktion cos x wie folgt umschreiben:
\[ - 2 (1 - \cos^2 x) - \cos x = - 1 \]Vereinfachen und umschreiben als:
\[ 2 \cos^{2} x - \cos x - 1 = 0 \]Faktorisieren Sie die linke Seite:
\[ (2 \cos x + 1)(\cos x - 1) = 0 \]Daher die beiden zu lösenden Gleichungen:
\[ (1) \quad 2 \cos x + 1 = 0 \quad \text{und} \quad (2) \quad \cos x - 1 = 0 \]Lösen Sie Gleichung (1) mit dem Referenzwinkel, wie in den obigen Beispielen gezeigt.
\[ \cos x = -\dfrac{1}{2} \] \[ x_{1} = \dfrac{2\pi}{3} + 2n\pi , \quad n = 0, \pm 1 , \pm 2, \ldots \] \[ x_{2} = \dfrac{4\pi}{3} + 2n\pi , \quad n = 0, \pm 1 , \pm 2, \ldots \]Lösen Sie Gleichung (2):
\[ \cos x = 1 \] \[ x_{3} = 2n\pi , \quad n = 0, \pm 1 , \pm 2, \ldots \]