Kreis- und Trigonometrieprobleme mit Lösungen | Mathematik Klasse 12
Willkommen zu dieser Sammlung von Sektor- und Kreis-Trigonometrieproblemen, die für Mathematikschüler der 12. Klasse entwickelt wurden. Jedes Problem konzentriert sich auf wichtige Konzepte wie Bogenlänge, Mittelpunktswinkel, Koordinaten von Punkten auf einem Kreis und Anwendungen trigonometrischer Funktionen. Detaillierte, Schritt-für-Schritt-Lösungen werden bereitgestellt, um Schülern zu helfen, ihr Verständnis von Kreisgeometrie und Trigonometrie zu vertiefen.
Koordinaten und Winkel in Normalposition
Bei der Lösung der folgenden Probleme werden wir die Definition der trigonometrischen Funktionen des Winkels \( \theta \) anhand der Koordinaten des Punktes \( P(x , y) \), der auf der Endseite eines Winkels \( \theta \) liegt, verwenden.
\[ \cos(\theta) = \dfrac{x}{R} \quad \tan(\theta) = \dfrac{y}{x} \quad \sec(\theta) = \dfrac{R}{x} \]
\[ \sin(\theta) = \dfrac{y}{R} \quad \cot(\theta) = \dfrac{x}{y} \quad \csc(\theta) = \dfrac{R}{y} \]
\[ R = \sqrt{x^2 + y^2} \]
Wir werden auch die Beziehung zwischen der Bogenlänge \( S \), dem Radius \( R \) und dem Mittelpunktswinkel \( \theta \) eines
Sektors verwenden: \[ S = R \theta \quad , \quad \text{mit } \theta \text{ im Bogenmaß} \]
Problem 1 - Bogenlänge und Koordinaten auf einem Kreis
Gegeben ist, dass die Koordinaten von Punkt \( A \), der sich auf dem untenstehenden Kreis befindet, \( (8, 0) \) sind und der Bogen \( s \) eine Länge von 20 Einheiten hat, bestimmen Sie die Koordinaten von Punkt \( P \) wie im Diagramm unten dargestellt.
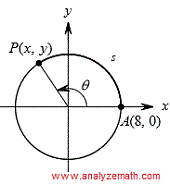
Schritt 1: Verwenden Sie die Bogenlängenformel, um den Winkel \( \theta \) im Bogenmaß zu finden.
Der Radius \( R \) des Kreises beträgt 8. Die Formel für die Bogenlänge \( s \) lautet:
\[ s = R \theta \]Wir haben \( s = 20 \), also:
\[ 20 = 8 \theta \] \[ \theta = \dfrac{20}{8} = 2.5 \text{ rad} \]Schritt 2: Verwenden Sie Sinus und Kosinus, um die Koordinaten von Punkt \( P \) zu finden.
\[ x = R \cos(\theta) = 8 \cos(2.5) \approx -6.40 \] \[ y = R \sin(\theta) = 8 \sin(2.5) \approx 4.79 \]Schlussfolgerung: Die Koordinaten von Punkt \( P \) sind ungefähr:
\[ P(-6.40, \, 4.79) \]Problem 2 - Bogenlänge unter Verwendung von Tangens und Radius
In einem rechtwinkligen Koordinatensystem verläuft ein Kreis mit seinem Mittelpunkt im Ursprung durch den Punkt \((4\sqrt{2},\ 5\sqrt{2})\).
Wie lang ist der Bogen \( S \), der in der folgenden Abbildung dargestellt ist?

Wir verwenden die Definition des Tangens, um den Winkel \( \theta \) zu finden.
\[ \tan(\theta) = \dfrac{y}{x} = \dfrac{5\sqrt{2}}{4\sqrt{2}} = \dfrac{5}{4} \] \[ \theta = \arctan\left(\dfrac{5}{4}\right) \]Verwenden Sie nun die Formel für die Bogenlänge \( s \) in Abhängigkeit von \( \theta \) und dem Radius \( R \).
\[ s = R\theta = \sqrt{(4\sqrt{2})^2 + (5\sqrt{2})^2} \cdot \arctan\left(\dfrac{5}{4}\right) \approx 8.11 \text{ Einheiten} \]Problem 3 - Minutenzeiger einer Uhr und Bogenlänge
Die Länge des Minutenzeigers einer Uhr beträgt \( 4.5 \, \text{cm} \). Finden Sie die Länge des Bogens, der von der Spitze des Minutenzeigers zwischen 23:10 Uhr und 23:50 Uhr zurückgelegt wird.
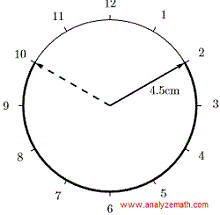
Von 23:10 bis 23:50 beträgt die Zeitdifferenz:
\[ 40 \text{ Minuten} \]Eine vollständige Umdrehung des Minutenzeigers entspricht 60 Minuten und einem Winkel von \( 360^{\circ} \), daher beträgt die Winkelverschiebung pro Minute:
\[ \dfrac{360^\circ}{60} = 6^\circ \text{ pro Minute} \] \[ \theta = 6^\circ \times 40 = 240^\circ \] \[ S = R \theta = 4.5 \times \left( \dfrac{240 \pi}{180} \right) = 6\pi \, \text{cm} \]Problem 4 - Kreisgeometrie mit mehreren Punkten
Die Punkte \( P(a, b) \), \( Q(5, 0) \) und \( M(c, -1) \) liegen auf einem Kreis mit Mittelpunkt \( O(0, 0) \) und einem Radius \( R = 5 \) Einheiten, wie unten dargestellt.

a) Die Koordinaten \( (a,b) \) von Punkt \( P \).
b) Die Bogenlänge zwischen \( Q \) und \( P \) im Gegenuhrzeigersinn.
c) Die x-Koordinate \( c \) von Punkt \( M \).
d) Winkel \( \theta \).
a)
\[ a = R \cos(35^\circ) = 5 \cos(35^\circ), \quad b = R \sin(35^\circ) = 5 \sin(35^\circ) \]b)
\[ \text{Bogen } PQ = R \cdot \dfrac{35 \pi}{180} = 5 \cdot \dfrac{35 \pi}{180} \approx 3.05 \text{ Einheiten} \]c)
\[ \sqrt{c^2 + (-1)^2} = 5 \quad \Rightarrow \quad c^2 + 1 = 25 \quad \Rightarrow \quad c^2 = 24 \] \[ c = \pm 2\sqrt{6} \] Da \( M \) im III. Quadranten liegt: \[ M(-2\sqrt{6}, -1) \]d)
\[ \tan(\theta + 35^\circ) = \dfrac{-1}{-2\sqrt{6}} = \dfrac{1}{2\sqrt{6}} \] \[ \theta + 35^\circ = 180^\circ + \tan^{-1}\left(\dfrac{1}{2\sqrt{6}}\right) \] \[ \theta = 180^\circ + \tan^{-1}\left(\dfrac{1}{2\sqrt{6}}\right) - 35^\circ \approx 156.54^\circ \]Problem 5 - Bogenlänge und Abstand in einem Kreis
Ein Kreis mit Radius \( R = 4 \) Einheiten und Mittelpunkt \( O \) ist unten dargestellt.
a) Finden Sie die Länge des Bogens zwischen den Punkten \( D \) und \( P \) im Uhrzeigersinn.
b) Finden Sie die Koordinaten \( (a , b) \) von Punkt \( P \).
c) Finden Sie die Länge der Strecke \( PD \).

a)
\[ \text{Bogen } DP = R \cdot \dfrac{130\pi}{180} = 4 \cdot \dfrac{130\pi}{180} \approx 9.08 \text{ Einheiten} \]b)
\[ a = 4 \cos(130^\circ), \quad b = 4 \sin(130^\circ) \]c)
\[ PD = \sqrt{(4 \cos(130^\circ) - 4)^2 + (4 \sin(130^\circ))^2} \approx 7.25 \]Problem 6 - Bogenlänge und Koordinaten auf einem Kreis
In einem Kreis mit Mittelpunkt \( O \) und Radius \( R = 3 \) ist die Bogenlänge \( S \) zwischen den Punkten \( A \) und \( B \) gegeben als \[ S = 12.5 \text{ Einheiten}. \] Finden Sie die Koordinaten \( (a, b) \) von Punkt \( B \).

Problem 7 - Bogenlänge aus Koordinaten
Punkt \( P \) hat die Koordinaten \( (4.1 , b) \) und befindet sich auf dem Kreis mit Mittelpunkt \( O \) und Radius \( R = 5 \) im I. Quadranten. Finden Sie die Länge des Bogens \( S \).
