Das Skalarprodukt (oder Punktprodukt) und das Kreuzprodukt von 3D-Vektoren werden definiert und ihre Eigenschaften werden diskutiert und zur Lösung von 3D-Problemen verwendet.
Skalar- (oder Punkt-) Produkt von zwei Vektoren
Das Skalar- (oder Punkt-) Produkt von zwei Vektoren \( \vec{u} \) und \( \vec{v} \) ist eine skalare Größe, definiert durch:
wobei \( || \vec{u} || \) die Länge des Vektors \( \vec{u} \) ist, \( || \vec{v} || \) die Länge des Vektors \( \vec{v} \) ist und \( \theta \) der Winkel zwischen den Vektoren \( \vec{u} \) und \( \vec{v} \) ist.
Wenn die Komponenten der Vektoren \( \vec{u} \) und \( \vec{v} \) bekannt sind: \( \vec{u} = (u_x , u_y ,u_z)\) und \( \vec{v} = (v_x , v_y , v_z) \), kann das Skalarprodukt wie folgt ausgedrückt werden:
Finden Sie \( a \) so, dass die Vektoren \( \lt a,-6,3 \gt \) und \( \lt 1,0,-2> \) senkrecht zueinander stehen.
Lösung
Damit zwei Vektoren senkrecht zueinander stehen, muss ihr Skalarprodukt gleich Null sein.
\( \lt a,-6,3 \gt \cdot \lt 1,0,-2> = a(1) + (-6)(0)+(3)(-2) = a - 6 = 0 \)
Lösen Sie nach a auf
\( a = 6\)
Skalar- und Vektorprojektion eines Vektors auf einen anderen
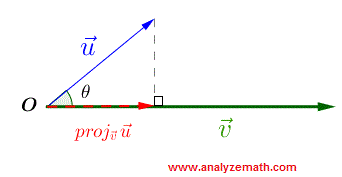
In vielen Anwendungen ist es wichtig, die Komponente eines Vektors in Richtung eines anderen Vektors zu finden. Wie unten gezeigt, wird der Vektor \( \vec{u}\) auf den Vektor \( \vec{v}\) projiziert, indem man senkrecht von der Endpunkt von \( \vec{u}\) zur Linie durch \( \vec{v}\) abfällt. Die Komponente von \( \vec{u}\) entlang \( \vec{v}\) ist eine Skalare Größe, die als Skalarprojektion bezeichnet wird und durch
.
Die Vektorprojektion von \( \vec{u}\) auf \( \vec{v}\) ist eine Vektorgröße, die erhalten wird, indem man die Komponente \( \text{comp}_{\vec{v}}\vec{u} \) mit dem Einheitsvektor in Richtung des Vektors \( \vec{v}\) multipliziert, und ist gegeben durch
Das Kreuz- (oder Vektor-) Produkt von zwei Vektoren \( \vec{u} = (u_x , u_y ,u_z)\) und \( \vec{v} = (v_x , v_y , v_z) \) ist eine Vektorgröße, definiert durch:
Das Kreuzprodukt \( \vec{u} \times \vec{v} \) steht senkrecht sowohl zu \( \vec{v} \) als auch zu \( \vec{u} \)
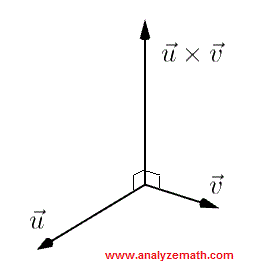
Die Regel der rechten Hand, um die Richtung des Kreuzprodukts zu finden, lautet wie folgt: Zeige mit dem Zeigefinger in Richtung \( \vec {u} \), mit dem Mittelfinger in Richtung \( \vec{v} \) und die Richtung des Kreuzprodukts \( \vec {u} \times \vec {v} \) ist in dieselbe Richtung wie der Daumen.
Sätze über Kreuzprodukte
Wenn \( \vec{u} \), \( \vec{v} \) und \( \vec{w} \) Vektoren sind und k eine Skalar ist, dann
1) Das Kreuzprodukt \( \vec{u} \times \vec{v} \) steht senkrecht sowohl zu \( \vec{v} \) als auch zu \( \vec{u} \)
2) \( \vec{u} \times \vec{v} = - \vec{v} \times \vec{u} \)
3) \( \vec{u} \times \vec{v} = 0 \) genau dann, wenn \( \vec{u} \) und \( \vec{v} \) parallel sind, wenn sowohl \( \vec{u} \) als auch \( \vec{v} \) nicht-Null-Vektoren sind.
4) \( \vec{u} \times (\ \vec{v} + \vec{w} ) = \vec{v} \times \vec{u} + \vec{u} \times \vec{w} \)
5) \( (k \vec{u}) \times \vec{v} = \vec{u} \times ( k\vec{v}) = k ( \vec{u} \times \vec{v} ) \)
6) \( ||\vec{u} \times \vec{v} || = ||\vec{u}|| ||\vec{v}|| sin \theta\) , wobei \( \theta \) der Winkel zwischen \( \vec{u}\) und \( \vec{v} \) ist.
Fläche eines Parallelogramms
Ein Parallelogramm ist ein Viereck (4 Seiten) mit gegenüberliegenden Seiten, die parallel sind. Im folgenden Bild ist das Parallelogramm A, B, C und D dargestellt. Daher gilt Gleichheit zwischen den Vektoren.
\( \vec{AB} = \vec{DC} \) und \( \vec{AD} = \vec{BC} \)
Die Fläche des Parallelogramms wird durch \( || \vec{AB} \times \vec{AD} || \) gegeben.
Die Fläche eines Dreiecks kann als die Hälfte der Fläche des entsprechenden Parallelogramms berechnet werden.
Volumen eines Parallellepiped
Ein Parallellepiped ist eine 3D-Figur, die durch 6 Parallelogramme gebildet wird, wie im folgenden Bild gezeigt. Es besteht Gleichheit zwischen verschiedenen Vektoren.
\( \vec{AE} = \vec{DH} = \vec{CG} = \vec{BF} = \vec{u} \)
\( \vec{AD} = \vec{BC} = \vec{EH} = \vec{FG} = \vec{v}\)
\( \vec{AB} = \vec{DC} = \vec{EF} = \vec{HG} = \vec{w}\)
Das Volumen V des Parallellepipeds ist gegeben durch
V \( = |\vec{u}\cdot (\vec{v} \times \vec{w})| = | \vec{v}\cdot (\vec{w} \times \vec{u})| = | \vec{w}\cdot (\vec{v} \times \vec{u})| \)
Beispiel 3
Berechnen Sie das Vektorprodukt der Vektoren \(\vec{u} = \lt 1,1,3 >\) und \(\vec{v} = \lt 1,0,2 > \).
Finden Sie zwei Einheitsvektoren, die senkrecht zu den Vektoren \( \vec{u} = \lt 1,-2,1 \gt \) und \( \vec{v} = \lt -2,0,4> \) stehen.
Lösung
Das Vektorprodukt \( \vec{w} = \vec{u} \times \vec{v} \) ist ein Vektor senkrecht zu beiden Vektoren \( \vec{u} \; \text{und} \; \vec{v} \).
Berechnen wir \( \vec{u} \times \vec{v} \) wie folgt:
Wir müssen nun einen Einheitsvektor \( \vec{u_1} \) in dieselbe Richtung wie \( \vec{w} \) finden, der gegeben ist durch
\( \vec{u_1} = \dfrac{1}{||\vec{w}||} \vec{w}\)
und einen zweiten Einheitsvektor \( \vec{u_2} \) in entgegengesetzter Richtung von \( \vec{w} \), der gegeben ist durch
\( \vec{u_2} = -\vec{u_1}\)
\( ||\vec{w}|| = \sqrt{(-8)^2+(- 6)^2+(- 4)^2 } = 2\sqrt{29}\)
\( \vec{u_1} = \dfrac{1}{2\sqrt{29}} (-8\vec{i} - 6 \vec{j} - 4 \vec{k}) = -\dfrac{4}{\sqrt{29}}\vec{i} -\dfrac{3}{\sqrt{29}}\vec{j}-\dfrac{2}{\sqrt{29}}\vec{k}\)
\( \vec{u_2} = \dfrac{4}{\sqrt{29}}\vec{i} + \dfrac{3}{\sqrt{29}}\vec{j}+ \dfrac{2}{\sqrt{29}}\vec{k}\)
Beispiel 5
Erklären Sie, warum die folgenden Aussagen nicht wahr sind.
a) \( \vec{u} \times \vec{u} = ||\vec{u}||^2\)
b) \( \vec{u} \cdot (\vec{u} \times \vec{w} )= (\vec{u} \cdot \vec{u}) \times \vec{w} \)
Lösung
a) Die linke Seite \( \vec{u} \times \vec{u} \) ist ein Vektorprodukt, und das Ergebnis ist ein Vektor. Die rechte Seite \( ||\vec{u}||^2\) ist eine skalare Größe. Ein Vektor und eine Skalargröße können nicht verglichen werden.
b) Die linke Seite \( \vec{u} \cdot (\vec{u} \times \vec{w} ) \) ist das Skalarprodukt von \( \vec{u} \) und \( (\vec{u} \times \vec{w} ) \) und das Ergebnis ist eine skalare Größe. Die rechte Seite ist das Produkt einer skalaren Größe \( \vec{u} \cdot \vec{u} \) und des Vektors \( \vec{w} \), und das Ergebnis ist ein Vektor. Eine skalare Größe und ein Vektor können nicht verglichen werden.
Beantworten Sie die folgenden Fragen
Detaillierte Lösungen und Erklärungen zu diesen Fragen.
1) Berechnen Sie \( \vec{u} \cdot (\vec{u} \times \vec{v}) \) unter der Annahme, dass \( \vec{u} = \lt a,b,c \gt \) und \( \vec{v} = \lt d,e,f \gt \) sind.
2) Finden Sie \( k \) so, dass die Vektoren \( \vec{u} = \lt -2,-k,1 \gt \) und \( \vec{v} = \lt 8,-2,-3 > \) senkrecht zueinander stehen.
3) Finden Sie \( k \) so, dass die Vektoren \( \vec{u} = \lt -3,2,-2 \gt \), \( \vec{v} = \lt 2,1,k> \) und \( \vec{w} = \lt -1,3,-5> \) in der gleichen Ebene (oder koplanar) liegen.
4) Finden Sie den Winkel \( \theta \) zwischen den Vektoren \( \vec{u} = \lt 2,0,1 \gt \) und \( \vec{v} = \lt 8,-2,-3 > \).
5) Finden Sie die Vektorprojektion von \( \vec{u} = \lt -1,-1,1 \gt \) auf \( \vec{v} = \lt 2,1,1 > \).
6) Finden Sie \( k \) so, dass die Punkte \( A(-1,2,k) \), \( B(-3,6,3) \) und \( C(1,3,6) \) die Eckpunkte eines rechtwinkligen Dreiecks mit einem rechten Winkel bei \( A \) sind.
7) Gegeben sei der Vektor \( \vec{v} = \lt 3,-1,-2 \gt \), finden Sie den Vektor \( \vec{u} \) so, dass \( \vec{v} \times \vec{u} = \lt 4,2,5 > \) und \( ||\vec{u}|| = 3 \).
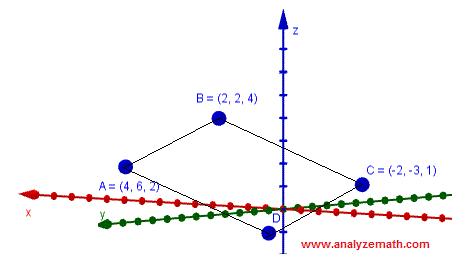
8) Punkte A, B, C und D bilden ein Parallelogramm.
a) Finden Sie die Koordinaten von Punkt D.
b) Finden Sie den Flächeninhalt des Parallelogramms.
9) In dem Würfel unten finden Sie den Winkel zwischen den Diagonalen AG und BH.
10) Finden Sie einen Vektor, der senkrecht zur Ebene liegt, die durch die Punkte A(1,2,-3), B(0,-2,1) und C(-2,0,1) definiert ist.
11) Finden Sie den Flächeninhalt des Dreiecks, dessen Eckpunkte die Punkte A(1,0,-3), B(1,-2,0) und C(0,2,1) sind.
12) Finden Sie das Volumen des unten gezeigten Parallelipipeds.
