Der Satz von Bayes zum Finden von bedingten Porbabilitäten wird erklärt und zur Lösung von Beispielen einschließlich ausführlicher Erklärungen verwendet. Diagramme werden verwendet, um den Satz visuell zu erklären.
Außerdem werden die erhaltenen numerischen Ergebnisse diskutiert, um die möglichen Anwendungen des Theorems zu verstehen.
\( P(A) P(E_i | A) = P(E_i) P(A | E_i) \)
was gibt
\( P(E_i | A) = \dfrac{P(E_i) P(A | E_i)}{P(A)} \)
Ersetzen Sie \( P(A) \) durch die obige Summe, um den Satz von Bayes wie folgt zu schreiben
\[ P(E_i | A) = \dfrac{P(E_i) P(A | E_i)}{\sum_{i=1}^{n} P(A | E_i) P(E_i)} \]
Verwendung von Bayes‘ Thereom-Beispielen mit detaillierten Lösungen
Das folgende Beispiel 1 soll die Verwendung des Satzes von Bayes erläutern und auch die durch den Satz gegebenen Ergebnisse interpretieren.
Beispiel 1
Eine von zwei Schachteln enthält 4 rote und 2 grüne Kugeln und die zweite Schachtel enthält 4 grüne und zwei rote Kugeln. Die Wahrscheinlichkeit, Box 1 oder Box 2 zufällig auszuwählen, beträgt konstruktionsbedingt 1/3 für Box 1 und 2/3 für Box 2.
Eine Box wird zufällig ausgewählt und daraus wird zufällig eine Kugel ausgewählt.
a) Wie hoch ist die Wahrscheinlichkeit, dass der ausgewählte Ball rot ist, dass er aus dem ersten Feld ausgewählt wurde?
b) Wie groß ist die Wahrscheinlichkeit, dass der ausgewählte Ball rot ist und aus dem zweiten Feld ausgewählt wurde?
c) Vergleichen Sie die Ergebnisse in Teil a) und b) und erläutern Sie die Antwort.
Lösung zu Beispiel 1
Nennen wir die erste Box B1 und die zweite Box B2
Event E1 sei „Auswahlbox 1“ und Ereignis E2 „Auswahlbox 2“.
Das Ereignis R sei „wähle einen roten Ball“.
Alle oben genannten Informationen sind im Diagramm unten enthalten.
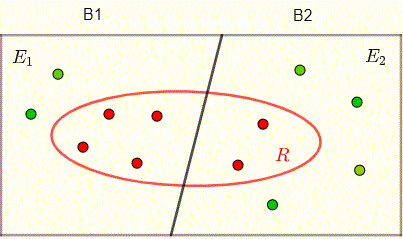
Die Wahrscheinlichkeiten für die Auswahl eines der beiden Kästchen wären (oben) gegeben durch
\( P(E_1) = 1/3\) und \( P(E_2) = 2/3 \)
Die bedingte Wahrscheinlichkeit, dass ein ausgewählter Ball rot ist, vorausgesetzt, dass er aus Feld 1 ausgewählt wurde, ist gegeben durch
\( P(R | E_1) = 4/6 = 2/3\) , 4 von 6 Bällen sind in Box 1 rot
Die bedingte Wahrscheinlichkeit, dass ein ausgewählter Ball rot ist, sofern er aus Feld 2 ausgewählt wurde, ist gegeben durch
\( P(R | E_2) = 2/6 = 1/3\) , 2 von 6 Bällen sind in Box 2 rot
a)
Die Frage besteht darin, die bedingte Wahrscheinlichkeit zu finden, dass der Ball aus Feld 1 ausgewählt wird, vorausgesetzt, dass er rot ist, gegeben durch den Satz von Bayes.
\( P(E_1|R) = \dfrac{P(R | E1) P(E1) }{ P(R | E1) P(E1) + P(R | E2) P(E2) } \)
\( = \dfrac{ 2/3 * 1/3}{2/3 * 1/3 + 1/3 * 2/3} = 1/2 \)
b)
Die Frage besteht darin, die bedingte Wahrscheinlichkeit zu finden, dass der Ball aus Feld 2 ausgewählt wird, vorausgesetzt, dass er rot ist, gegeben durch den Satz von Bayes.
\( P(E_2|R) = \dfrac{P(R | E2) P(E2) }{ P(R | E1) P(E1) + P(R | E2) P(E2) } \)
\( = \dfrac{ 1/3 * 2/3}{2/3 * 1/3 + 1/3 * 2/3} = 1/2 \)
c)
Die beiden in den Teilen a) und b) berechneten Wahrscheinlichkeiten sind gleich.
Obwohl sich in Kästchen 1 mehr rote Kugeln befinden als in Kästchen 2 (doppelt so viele), sind die oben berechneten Wahrscheinlichkeiten gleich, da die Wahrscheinlichkeit, Kästchen 2 auszuwählen, höher (doppelt so viel) ist als die Wahrscheinlichkeit, Kästchen 1 auszuwählen. Satz von Bayes berücksichtigt alle Informationen.
Beispiel 2
1 % der Bevölkerung leidet an einer bestimmten Krankheit und die restlichen 99 % sind frei von dieser Krankheit.
Zum Nachweis dieser Erkrankung dient ein Test. Dieser Test fällt bei 95 % der erkrankten Personen positiv aus und ist auch bei 2 % der erkrankten Personen (falsch) positiv.
Wenn eine zufällig aus dieser Population ausgewählte Person positiv getestet wurde, wie hoch ist dann die Wahrscheinlichkeit, dass sie an der Krankheit leidet?
Lösung zu Beispiel 2
Sei D das Ereignis „die Krankheit haben“ und FD das Ereignis „frei von der Krankheit“.
Das Ereignis TP sei das Ereignis, dass der „Test positiv“ ist.
Nachfolgend finden Sie ein Diagramm mit allen oben genannten Informationen.
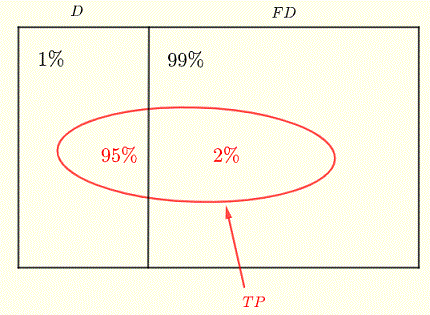
Die Wahrscheinlichkeit, dass eine Person an der Krankheit leidet, wenn sie positiv getestet wurde, ergibt sich aus dem Satz von Bayes:
\( P(D | TP) = \dfrac{P(TP | D) P(D) }{ P(TP | D) P(D) + P(TP | ND) P(ND) } \)
Auch wenn der Test bei einer Person positiv ausfällt, ist die Wahrscheinlichkeit, an der Krankheit zu erkranken, recht gering.
Erklärung
Beachten Sie, dass selbst wenn eine Person positiv getestet wird, dies nicht bedeutet, dass sie/er an der Krankheit leidet; und das liegt daran, dass die Zahl der krankheitsfreien (99 %) viel höher ist als die der krankheitsfreien
die Krankheit (1 %).
Lassen Sie uns die oben erzielten Ergebnisse anhand einiger konkreter Zahlen verdeutlichen.
Angenommen, 1000 Menschen werden getestet
krankheitsfrei sind: \( 99\% \times 1000 = 990\) und \( 2\% \times 990 = 19,8 \approx 20\) Test positiv
Menschen mit Krankheiten: \( 1\% \times 1000 = 10\) und \( 95\% \times 10 = 9,5 = 9,5 \approx 10\) Test positiv
Von allen positiv getesteten 20 + 10 = 30 nur 10 haben die Krankheit.
Der Prozentsatz derjenigen, die positiv getestet wurden, aber nicht an der Krankheit leiden, beträgt: 9,5 / (19,8 + 9,5) = 0,32
Das ist die oben berechnete Wahrscheinlichkeit \( P(D | TP) \).
Beispiel 3
Drei Fabriken produzieren Glühbirnen, um den Markt zu beliefern. Fabrik A produziert 20 %, 50 % der Werkzeuge werden in Fabrik B und 30 % in Fabrik C hergestellt.
2 % der in Fabrik A produzierten Glühbirnen, 1 % der in Fabrik B produzierten Glühbirnen und 3 % der in Fabrik C produzierten Glühbirnen sind defekt.
Auf dem Markt wird zufällig eine Glühbirne ausgewählt und als defekt befunden. Wie hoch ist die Wahrscheinlichkeit, dass diese Glühbirne von Fabrik B hergestellt wurde?
Lösung zu Beispiel 3
Es seien \( P(A) = 20\% \), \( P(B) = 50\% \) und \( P(C) = 30\% \) die Wahrscheinlichkeiten, aus denen eine zufällig ausgewählte Glühbirne stammt Fabrik A, B und C.
Sei \( P(D) \) die Wahrscheinlichkeit, dass eine defekte Glühbirne ausgewählt wird.
Es seien \( P(D | A) = 2\% \), \( P(D | B) = 1\% \) und \( P(D | C) = 3\%\) das Bedingte Wahrscheinlichkeiten, dass eine Glühbirne defekt ist, vorausgesetzt, dass sie aus Fabrik A, B bzw. C ausgewählt wurde.
Wir berechnen nun die bedingte Wahrscheinlichkeit, dass die Glühbirne von Fabrik B hergestellt wurde, vorausgesetzt, dass sie defekt ist, geschrieben als \(P(B | D) \) und gegeben durch den Satz von Bayes.
\( P(B | D) = \dfrac{P(D | B) P(B) }{ P(D | A) P(A) + P(D | B) P(B) + P(D | C) P(C)}\)
Obwohl Fabrik B 50 % der Glühbirnen produziert, ist die Wahrscheinlichkeit, dass die ausgewählte (defekte) Glühbirne aus dieser Fabrik stammt, gering, da die Wahrscheinlichkeit (1 %) der von dieser Fabrik produzierten Glühbirnen gering ist, defekt zu sein.
Beispiel 4
Ein Radarsystem ist so konzipiert, dass die Wahrscheinlichkeit, die Anwesenheit eines Flugzeugs in seiner Reichweite zu erkennen, 98 % beträgt. Befindet sich jedoch kein Flugzeug in seiner Reichweite, meldet es trotzdem (fälschlicherweise) mit einer Wahrscheinlichkeit von 5 %, dass ein Flugzeug anwesend ist. Die Wahrscheinlichkeit, dass sich ein Flugzeug jederzeit im Radarbereich befindet, beträgt 7 %.
a) Wie groß ist die Wahrscheinlichkeit, dass sich bei der Erkennung eines Flugzeugs kein Flugzeug im Radarbereich befindet?
b) Wie groß ist die Wahrscheinlichkeit, dass sich ein Flugzeug im Radarbereich befindet, wenn ein Flugzeug erkannt wird?
c) Wie groß ist die Wahrscheinlichkeit, dass sich ein Flugzeug im Radarbereich befindet, wenn kein Flugzeug erkannt wird?
d) Wie groß ist die Wahrscheinlichkeit, dass sich kein Flugzeug im Radarbereich befindet, sofern kein Flugzeug erkannt wird?
Lösung zu Beispiel 4
Wir werden die Komplementnotationen verwenden.
Sei \( A \) das Ereignis, dass ein Flugzeug vorhanden ist, und \( A^c \) das Ereigniskomplement von \( A \), was bedeutet, dass kein Flugzeug vorhanden ist.
Die Wahrscheinlichkeit für das Eintreten von A wird wie folgt angegeben:
\( P(A) = 7\% \)
Und
\( P(A^c) = 100\% - 7\% = 93\% \)
Sei \( D \) das Ereignis, dass ein Flugzeug vom Radarsystem erkannt wird, und \( D^c \) das Komplement von \( D \), was bedeutet, dass kein Flugzeug erkannt wird.
Die bedingte Wahrscheinlichkeit, dass ein Flugzeug erkannt wird, sofern es vorhanden ist, ist oben angegeben und wird wie folgt geschrieben:
\( P(D | A) = 98%\)
\( P(D | A^c) = 5% \)
a)
Tragen Sie alle oben genannten Informationen wie unten gezeigt in ein Venn-Diagramm ein.
Verwenden Sie den Satz von Bayes, um die Wahrscheinlichkeit zu beschreiben, dass sich bei der Erkennung eines Flugzeugs kein Flugzeug im Radarbereich befindet
b)
Verwenden Sie den Satz von Bayes, um die Wahrscheinlichkeit zu beschreiben, dass sich ein Flugzeug in der Reichweite des Radars befindet, sofern ein Flugzeug erkannt wird
\( P(A | D) = \dfrac{ P(D | A) P(A) }{ P(D | A) P(A) + P(D | A^c) P(A^c)} \)
c)
Wir müssen zunächst die folgenden Wahrscheinlichkeiten berechnen
\( P(D^c | A) = 100\% - 98\% = 2\% \)
\( P(D^c | A^c) = 100\% - 5\% = 95\% \)
Tragen Sie alle oben genannten Informationen wie unten gezeigt in ein Venn-Diagramm ein.
Verwenden Sie den Satz von Bayes, um die Wahrscheinlichkeit zu beschreiben, dass sich ein Flugzeug in der Reichweite des Radars befindet, vorausgesetzt, dass kein Flugzeug erkannt wird
d)
Verwenden Sie den Satz von Bayes, um die Wahrscheinlichkeit zu beschreiben, dass sich kein Flugzeug in der Reichweite des Radars befindet, vorausgesetzt, dass kein Flugzeug erkannt wird
HINWEIS
Alle oben genannten Berechnungen können mit Hilfe des unten gezeigten Baumdiagramms durchgeführt werden. Sobald das Baumdiagramm alle Wahrscheinlichkeiten enthält, ist es einfacher, diese Wahrscheinlichkeiten im Bayes-Theorem zu verwenden, um die Endergebnisse auszuwerten.
