Math Problems with Solutions for Grade 10

a) Maximum height occurs at the vertex of the parabola:
$$t = \frac{-b}{2a} = \frac{-15}{2(-5)} = \frac{15}{10} = 1.5\ \text{seconds}$$

b) Substitute $t = 1.5$ into the equation to obtain the maximum height:
$$h(1.5) = -5(1.5)^2 + 15(1.5) + 20 = -11.25 + 22.5 + 20 = 31.25\ \text{meters}$$

c) Set $h(t) = 0$:
$$-5t^2 + 15t + 20 = 0 \Rightarrow t^2 - 3t - 4 = 0$$
Factor:
$$(t - 4)(t + 1) = 0 \Rightarrow t = 4\ \text{or}\ t = -1$$
Time cannot be negative, hence the ball hits the ground $4$ seconds after it was thrown.

a) Let $d$ be the number of dimes and $q$ be the number of quarters.
Total number of coins is $30$:
$$d + q = 30 \quad \text{(1)}$$
A dime is worth $10$ cents and a quarter is worth $25$ cents, hence:
$$0.10d + 0.25q = 5.10 \quad \text{(2)}$$

b) From equation (1): $d = 30 - q$
Substitute into equation (2):
$$0.10(30 - q) + 0.25q = 5.10$$
Expand and simplify:
$$3 - 0.10q + 0.25q = 5.10$$
$$0.15q = 2.10$$
$$q = 14$$
Then $d = 16$.
You have $16$ dimes and $14$ quarters.

a) The radius is distance from the center to any point on the circle, hence the use of the distance formula to find the radius $r$ using the center $(3,-2)$ and the point $(6,2)$:
$$r = \sqrt{(6 - 3)^2 + (2 - (-2))^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$

b) The Equation of the circle is given by:
$$(x - 3)^2 + (y + 2)^2 = 25$$

Factor all expressions:
$$x^2 - 9 = (x - 3)(x + 3)$$
$$x^2 - x - 6 = (x - 3)(x + 2)$$

Now substitute in the given expression:
$$\frac{(x - 3)(x + 3)}{(x - 3)(x + 2)} \cdot \frac{x - 2}{x + 3}$$

Cancel common factors $(x - 3)$ and $(x + 3)$ to obtain:
$$\frac{x^2 - 9}{x^2 - x - 6} \cdot \frac{x - 2}{x + 3} = \frac{x - 2}{x + 2}$$

When we cancel common factors, as was done above, we are dividing by common factors. We cannot divide by zero, therefore we need to impose the conditions that the common factors canceled cannot be zero:
$$x - 3 \neq 0 \Rightarrow x \neq 3$$
$$x + 3 \neq 0 \Rightarrow x \neq -3$$

The given expression simplifies to:
$$\frac{x - 2}{x + 2}, \quad \text{where } x \neq 3,\ -3$$

Square both sides:
$$(\sqrt{2x + 3})^2 = (x - 1)^2$$
$$2x + 3 = x^2 - 2x + 1$$

Rearrange:
$$0 = x^2 - 4x - 2$$

Use the quadratic formula:
$$x = \frac{4 \pm \sqrt{(-4)^2 - 4(1)(-2)}}{2(1)} = \frac{4 \pm \sqrt{16 + 8}}{2}$$
$$= \frac{4 \pm \sqrt{24}}{2} = \frac{4 \pm 2\sqrt{6}}{2} = 2 \pm \sqrt{6}$$

Check for extraneous solutions:

Try $x = 2 + \sqrt{6} \approx 4.45$:
LHS = $\sqrt{2(4.45) + 3} = \sqrt{11.9} \approx 3.45$
RHS = $4.45 - 1 = 3.45$ (Valid)

Try $x = 2 - \sqrt{6} \approx -0.45$:
LHS = $\sqrt{2(-0.45) + 3} = \sqrt{-0.9 + 3} = \sqrt{2.1} \approx 1.45$
RHS = $-0.45 - 1 = -1.45$ (Invalid)

The solution $x = 2 + \sqrt{6}$ verifies both sides of the given equation but $x = 2 - \sqrt{6}$ does not and is therefore an extraneous solution.

The solution to the given equation is: $$x = 2 + \sqrt{6}$$

Find the slope of $AB$ and $CD$:
$$m_{AB} = \frac{7 - 3}{6 - 2} = \frac{4}{4} = 1$$
$$m_{CD} = \frac{5 - 1}{10 - 6} = \frac{4}{4} = 1$$

Find the slope of $BC$ and $AD$:
$$m_{BC} = \frac{5 - 7}{10 - 6} = \frac{-2}{4} = -0.5$$
$$m_{AD} = \frac{1 - 3}{6 - 2} = \frac{-2}{4} = -0.5$$

Since both pairs of opposite sides are parallel, ABCD is a parallelogram.

First, express 625 as a power of 5:
$$625 = 5^4$$

Use exponent rules to write:
$$\dfrac{5^{2x}}{5} = 5^{2x-1}$$

Rewrite the equation:
$$5^{2x - 1} = 5^4$$

Which gives the algebraic equation:
$$2x - 1 = 4$$

Solve for $x$:
$$x = \frac{5}{2}$$

Use the Cosine Law:
$$c^2 = a^2 + b^2 - 2ab\cos(C)$$
$$c^2 = 7^2 + 10^2 - 2(7)(10)\cos(120^\circ)$$
$$c^2 = 49 + 100 - 140(-0.5)$$
$$c^2 = 149 + 70 = 219$$
$$c = \sqrt{219} \approx 14.8 \ \text{cm}$$

Substitute $x = 4$, $f(x) = 15$ into the equation:
$$15 = a(4 - 2)^2 + 3$$

Solve for $a$:
$$15 = a(2)^2 + 3$$
$$a = 3$$

Function $f(x)$ is a quadratic function given by:
$$f(x) = 3(x - 2)^2 + 3$$

From the vertex form $a(x - h)^2 + k$, the vertex is $(h, k) = (2, 3)$.

a) Let $h$ be the height of the tower. Use the tangent formula in a right triangle:
$$\tan(32^\circ) = \frac{h}{50}$$
Solve for $h$:
$$h = 50 \cdot \tan(32^\circ) \approx 50 \cdot 0.6249 = 31.2\ \text{m}$$

b) Height of the drone: $31.2 + 30 = 61.2$
Let $\theta$ be the angle of elevation to the drone:
$$\tan(\theta) = \frac{61.2}{50}$$
$$\theta = \tan^{-1}(1.224) \approx 50.8^\circ$$

Let:
$S$ be the speed of the boat in still water (in km/h),
$r$ be the speed of the river current (in km/h),
$d$ be the distance between points A and B (in km).

From the given: Downstream:
$$d = 3(S + r)$$
Upstream:
$$d = 5(S - r)$$

Equating both expressions for $d$:
$$3(S + r) = 5(S - r)$$

Expand both sides:
$$3S + 3r = 5S - 5r$$

Put terms with $r$ on one side and terms with $S$ on the other side:
$$8r = 2S$$

Solve for $r$:
$$r = \frac{S}{4}$$

Now substitute $r = \frac{S}{4}$ back into the equation for downstream:
$$d = 3\left(S + \frac{S}{4}\right) = 3\left(\frac{5S}{4}\right) = \frac{15S}{4}$$

Now, in still water (no current), the speed is just $S$. Time to travel from A to B in still water:
$$\text{Time} = \frac{d}{S} = \frac{\frac{15S}{4}}{S} = \frac{15}{4} = 3.75 \text{ hours}$$

So, the time it would take the boat to go from A to B in still water is $3 \text{ hours and } 45 \text{ minutes}$.

Expand the function:
$$f(x) = -3(x^2 - 14x + 40) = -3x^2 + 42x - 120$$

This is a quadratic function of the form $f(x) = ax^2 + bx + c$ where $a = -3, \, b = 42$.

The function reaches its maximum at the vertex whose x-coordinate is given by:
$$x = -\frac{b}{2a} = -\frac{42}{2(-3)} = \frac{42}{6} = 7$$

To find the maximum value, substitute $x = 7$ back into the function:
$$f(7) = -3(7 - 10)(7 - 4) = -3(-3)(3) = -3 \cdot -9 = 27$$

The function has a maximum at $x = 7$ and the maximum value of $f(x)$ is $f(7) = 27$.

Let $n$ be the number of students who scored below 60 and $N$ be the number of students who scored 60 or more.

The average for students who scored below 60 is:
$$\frac{\sum X_i}{n} = 50 \Rightarrow \sum X_i = 50n$$

The average for students who scored 60 or more is:
$$\frac{\sum Y_i}{N} = 75 \Rightarrow \sum Y_i = 75N$$

The overall class average is 70:
$$\frac{\sum X_i + \sum Y_i}{20} = 70$$

Substitute:
$$\frac{50n + 75N}{20} = 70$$

Multiply all terms by 20 and simplify:
$$50n + 75N = 1400 \quad \text{(1)}$$

We also have:
$$n + N = 20 \Rightarrow N = 20 - n$$

Substitute $N$ into equation (1):
$$50n + 75(20 - n) = 1400$$

Expand and simplify:
$$-25n + 1500 = 1400$$

Solve for $n$:
$$-25n = -100 \Rightarrow n = 4$$

$n = 4$ students who scored below 60.

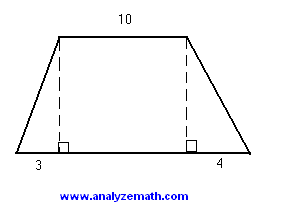Let $h$ be the height of the trapezoid.
$$\text{Area} = \frac{1}{2} \cdot h \cdot (\text{base}_1 + \text{base}_2) = \frac{1}{2} \cdot h \cdot (10 + 10 + 3 + 4) = 270$$

Solve for $h$:
$$\frac{1}{2} \cdot h \cdot 27 = 270 \Rightarrow h = 20$$

Apply the Pythagorean Theorem to the right triangle on the left (hypotenuse $L$):
$$20^2 + 3^2 = L^2 \Rightarrow L = \sqrt{409}$$

Apply the Pythagorean Theorem to the right triangle on the right (hypotenuse $R$):
$$20^2 + 4^2 = R^2 \Rightarrow R = \sqrt{416}$$

The perimeter of the trapezoid is:
$$\text{Perimeter} = \sqrt{409} + 10 + \sqrt{416} + 17 = 27 + \sqrt{409} + \sqrt{416} \approx 68 \text{ units}$$

Let the length be $L$ meters and the width be $W$ meters such that $L > W$.

Use the area to write:
$$L \times W = 300$$

Use the perimeter to write:
$$2L + 2W = 70$$

Divide all terms by 2:
$$L + W = 35$$

Solve for $L$:
$$L = 35 - W$$

Substitute into the area equation:
$$(35 - W) \cdot W = 300$$

Expand and rearrange into standard quadratic form:
$$35W - W^2 = 300$$
$$W^2 - 35W + 300 = 0$$

Solve using the quadratic formula:
$$W = \frac{35 \pm \sqrt{(-35)^2 - 4(1)(300)}}{2(1)}$$
$$W = \frac{35 \pm \sqrt{1225 - 1200}}{2} = \frac{35 \pm \sqrt{25}}{2} = \frac{35 \pm 5}{2}$$

$$W = 20 \text{ or } W = 15$$

For $W = 15$, $L = 35 - 15 = 20$.
For $W = 20$, $L = 35 - 20 = 15$.

Since $L > W$, the rectangle has dimensions $L = 20$ and $W = 15$.

The motor has a speed of $3000$ revolutions per minute.
1 revolution is $360^\circ$
1 minute is $60$ seconds

Use dimensional analysis:
$$\frac{3000 \, \text{rev}}{1 \, \text{min}} \times \frac{360^\circ}{1 \, \text{rev}} \times \frac{1 \, \text{min}}{60 \, \text{sec}}$$

Cancel the units to obtain degrees per second:
$$= \frac{3000 \times 360}{60} = \frac{1,080,000}{60} = 18,000^\circ \, \text{per second}$$

Let $x$ be the selling price of the house.
$$6\% \text{ of } x = 8,880$$
$$0.06x = 8,880$$

Solve for $x$:
$$x = \frac{8,880}{0.06}$$
$$x = 148,000$$

The selling price of the house was $\$148,000$.

We are given:
Rotational speed: $400 \, \text{rev/min}$
Linear speed: $72 \, \text{km/h} = 72,000 \, \text{m/h}$

First, convert revolutions per minute to revolutions per hour:
$$400 \, \dfrac{\text{rev}}{\text{min}} \times 60 \, \dfrac{\text{min}}{\text{h}} = 24,000 \, \dfrac{\text{rev}}{\text{h}}$$

Let $C$ be the circumference of the tire in meters. The total distance traveled in one hour is equal to the number of revolutions per hour multiplied by the circumference:
$$24,000 \cdot C = 72,000$$

Solving for $C$:
$$C = \frac{72,000}{24,000} = 3 \, \text{meters}$$

Let $x$ be the cost of one shirt, $y$ be the cost of one pair of trousers, and $z$ be the cost of one hat. We are given:
(1) $4x + 4y + 2z = 560$
(2) $9x + 9y + 6z = 1290$

Divide equation (2) by 3:
(3) $3x + 3y + 2z = 430$

Now subtract equation (1) from equation (3):
$$(3x + 3y + 2z) - (4x + 4y + 2z) = 430 - 560$$
$$-x - y = -130 \Rightarrow x + y = 130 \quad \text{(4)}$$

Substitute equation (4) into equation (3):
$$3(x + y) + 2z = 430$$
$$3(130) + 2z = 430$$
$$390 + 2z = 430$$
$$2z = 40 \Rightarrow z = 20$$

Now substitute back to find the total cost of 1 shirt, 1 pair of trousers, and 1 hat:
$$x + y + z = 130 + 20 = 150$$

The total cost is $\$150$.

Let $x$ represent the total number of toys.
The first child has $\frac{x}{10}$ toys.
The second child has $\frac{x}{10} + 12$ toys.
The third child has $\frac{x}{10} + 1$ toys.
The fourth child has $2 \left( \frac{x}{10} + 1 \right)$ toys.

We set up the equation for the total number of toys:
$$\frac{x}{10} + \left( \frac{x}{10} + 12 \right) + \left( \frac{x}{10} + 1 \right) + 2 \left( \frac{x}{10} + 1 \right) = x$$

Expand:
$$\frac{x}{10} + \frac{x}{10} + 12 + \frac{x}{10} + 1 + \frac{2x}{10} + 2 = x$$

Combine like terms:
$$\frac{5x}{10} + 15 = x$$
$$\frac{x}{2} + 15 = x$$

Subtract $\frac{x}{2}$ from both sides:
$$15 = \frac{x}{2}$$

Solve for $x$:
$$x = 30$$

Thus, the total number of toys is $30$.

First, we write each term in the product as a fraction:
$$\left( \frac{9}{10} \right) \left( \frac{10}{11} \right) \left( \frac{11}{12} \right) \cdots \left( \frac{99}{100} \right)$$

Now, observe the telescoping cancellation pattern. The numerator of each fraction cancels out the denominator of the previous fraction, leaving only the first numerator and the final denominator:

$$\frac{9}{100}$$