Circle and Trigonometry Problems with Solutions | Grade 12 Math
Welcome to this collection of sectors and circles trigonometry problems designed for Grade 12 math students. Each problem focuses on important concepts such as arc length, central angles, coordinates of points on a circle, and applications of trigonometric functions. Detailed, step-by-step solutions are provided to help students strengthen their understanding of circle geometry and trigonometry.
Coordinates and Angles in Standard Position
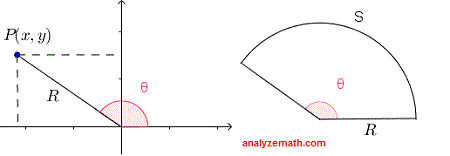
When solving the problems below, we will make use of the definition of the trigonometric functions of angle \( \theta \) in terms of the coordinates of point \( P(x , y) \) that is on the terminal side of an angle \( \theta \).
\[ \cos(\theta) = \dfrac{x}{R} \quad \tan(\theta) = \dfrac{y}{x} \quad \sec(\theta) = \dfrac{R}{x} \]
\[ \sin(\theta) = \dfrac{y}{R} \quad \cot(\theta) = \dfrac{x}{y} \quad \csc(\theta) = \dfrac{R}{y} \]
\[ R = \sqrt{x^2 + y^2} \]
We will also use the relationship between the arc length \( S \), the radius \( R \) and the central angle \( \theta \) of a
sector: \[ S = R \theta \quad , \quad \text{with } \theta \text{ in radians} \]
Problem 1 - Arc Length and Coordinates on a Circle
Given that the coordinates of point \( A \), located on the circle below, are \( (8, 0) \), and the arc \( s \) has a length of 20 units, determine the coordinates of point \( P \) as shown in the diagram below.
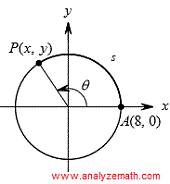
Step 1: Use the arc length formula to find the angle \( \theta \) in radians.
The radius \( R \) of the circle is 8. The formula for the arc length \( s \) is:
\[ s = R \theta \]We are given \( s = 20 \), so:
\[ 20 = 8 \theta \] \[ \theta = \dfrac{20}{8} = 2.5 \text{ radians} \]Step 2: Use sine and cosine to find the coordinates of point \( P \).
\[ x = R \cos(\theta) = 8 \cos(2.5) \approx -6.40 \] \[ y = R \sin(\theta) = 8 \sin(2.5) \approx 4.79 \]Conclusion: The coordinates of point \( P \) are approximately:
\[ P(-6.40, \, 4.79) \]Problem 2 - Arc Length Using Tangent and Radius
In a rectangular coordinate system, a circle with its center at the origin passes through the point \((4\sqrt{2},\ 5\sqrt{2})\).
What is the length of the arc \( S \) shown in the figure below?

We use the definition of tangent to find the angle \( \theta \).
\[ \tan(\theta) = \dfrac{y}{x} = \dfrac{5\sqrt{2}}{4\sqrt{2}} = \dfrac{5}{4} \] \[ \theta = \arctan\left(\dfrac{5}{4}\right) \]Now, use the formula for arc length \( s \) in terms of \( \theta \) and the radius \( R \).
\[ s = R\theta = \sqrt{(4\sqrt{2})^2 + (5\sqrt{2})^2} \cdot \arctan\left(\dfrac{5}{4}\right) \approx 8.11 units \]Problem 3 - Clock Minute Hand and Arc Length
The length of the minute hand of a clock is \( 4.5 \, \text{cm} \). Find the length of the arc traced by the tip of the minute hand between 11:10 PM and 11:50 PM.
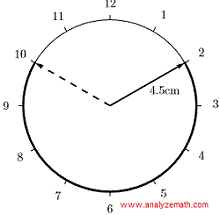
From 11:10 to 11:50, there is a time difference of:
\[ 40 \text{ minutes} \]One complete rotation of the minute hand corresponds to 60 minutes and an angle of \( 360^{\circ} \), so the angular displacement per minute is:
\[ \dfrac{360^\circ}{60} = 6^\circ \text{ per minute} \] \[ \theta = 6^\circ \times 40 = 240^\circ \] \[ S = R \theta = 4.5 \times \left( \dfrac{240 \pi}{180} \right) = 6\pi \, \text{cm} \]Problem 4 - Circle Geometry with Multiple Points
The points \( P(a, b) \), \( Q(5, 0) \), and \( M(c, -1) \) lie on a circle centered at \( O(0, 0) \) with a radius \( R = 5 \) units, as illustrated below.

a) The coordinates \( (a,b) \) of point \( P \).
b) The arc length between \( Q \) and \( P \) in counterclockwise direction.
c) The x-coordinate \( c \) of point \( M \).
d) Angle \( \theta \).
a)
\[ a = R \cos(35^\circ) = 5 \cos(35^\circ), \quad b = R \sin(35^\circ) = 5 \sin(35^\circ) \]b)
\[ \text{arc } PQ = R \cdot \dfrac{35 \pi}{180} = 5 \cdot \dfrac{35 \pi}{180} \approx 3.05 \, \text{ units} \]c)
\[ \sqrt{c^2 + (-1)^2} = 5 \quad \Rightarrow \quad c^2 + 1 = 25 \quad \Rightarrow \quad c^2 = 24 \] \[ c = \pm 2\sqrt{6} \] Since \( M \) is in quadrant III: \[ M(-2\sqrt{6}, -1) \]d)
\[ \tan(\theta + 35^\circ) = \dfrac{-1}{-2\sqrt{6}} = \dfrac{1}{2\sqrt{6}} \] \[ \theta + 35^\circ = 180^\circ + \tan^{-1}\left(\dfrac{1}{2\sqrt{6}}\right) \] \[ \theta = 180^\circ + \tan^{-1}\left(\dfrac{1}{2\sqrt{6}}\right) - 35^\circ \approx 156.54^\circ \]Problem 5 - Arc Length and Distance in a Circle
A circle with radius \( R = 4 \) units and center \( O \) is shown below.
a) Find the length of the arc between points \( D \) and \( P \) in clockwise direction.
b) Find the coordinates \( (a , b) \) of point \( P \).
c) Find the length of segment \( PD \).

a)
\[ \text{Arc } DP = R \cdot \dfrac{130\pi}{180} = 4 \cdot \dfrac{130\pi}{180} \approx 9.08 \, \text{ units} \]b)
\[ a = 4 \cos(130^\circ), \quad b = 4 \sin(130^\circ) \]c)
\[ PD = \sqrt{(4 \cos(130^\circ) - 4)^2 + (4 \sin(130^\circ))^2} \approx 7.25 \]Problem 6 - Arc Length and Coordinates on a Circle
In a circle with center \( O \) and radius \( R = 3 \), the arc length \( S \) between points \( A \) and \( B \) is given as \[ S = 12.5 \, \text{ units}. \] Find the coordinates \( (a, b) \) of point \( B \).

Problem 7 - Arc Length from Coordinates
Point \( P \) has coordinates \( (4.1 , b) \) and is located on the circle, of center \( O \) and radius \( R = 5 \), in quadrant I. Find the length of arc \( S \).
