Find a Polynomial Given its Graph Questions with Solutions
Learn how to determine a polynomial function from its graph. This page includes example questions with step-by-step solutions and clear explanations to help you understand the process.
Free Practice for SAT, ACT
and Compass Math tests
Question 1 - Cubic Polynomial with Multiple Roots
Find the equation of the cubic polynomial function \( g \) shown below.
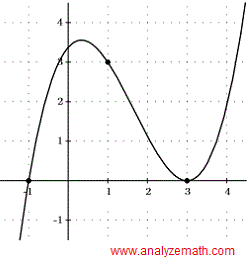
The graph of the function has one zero of multiplicity 1 at \( x = -1 \) which corresponds to the factor \( x + 1 \), and a zero of multiplicity 2 at \( x = 3 \) (graph touches but does not cut the x-axis) which corresponds to the factor \( (x - 3)^2 \), hence function \( g \) has the equation:
\[ g(x) = k(x + 1)(x - 3)^2 \]where \( k \) is a constant.
Constant \( k \) may be found using the point with coordinates \( (1, 3) \) shown in the graph.
\[ g(1) = k(1 + 1)(1 - 3)^2 = 3 \]Simplify and solve for \( k \).
\[ k = \dfrac{3}{8} \]\( g(x) \) is given by:
\[ g(x) = \dfrac{3}{8}(x + 1)(x - 3)^2 \]Question 2 - Fourth Degree Polynomial with Multiplicities
Find the fourth-degree polynomial function \( f \) whose graph is shown in the figure below.

The graph of the polynomial has a zero of multiplicity 1 at \( x = 2 \) which corresponds to the factor \( (x - 2) \), another zero of multiplicity 1 at \( x = -2 \) which corresponds to the factor \( (x + 2) \), and a zero of multiplicity 2 at \( x = -1 \) (graph touches but does not cut the x-axis) which corresponds to the factor \( (x + 1)^2 \), hence the polynomial \( f \) has the equation:
\[ f(x) = k(x - 2)(x + 2)(x + 1)^2 \]where \( k \) is a constant.
Constant \( k \) may be found using the y-intercept \( f(0) = -1 \) shown in the graph.
\[ f(0) = k(0 - 2)(0 + 2)(0 + 1)^2 = -1 \]Simplify and solve for \( k \).
\[ k = \dfrac{1}{4} \]\( f(x) \) is given by:
\[ f(x) = \dfrac{1}{4}(x - 2)(x + 2)(x + 1)^2 \]Question 3 - Degree 4 Polynomial with Different Multiplicities
Find the equation of the degree 4 polynomial \( f \) graphed below.

The graph has \( x \)-intercepts at \( x = 0 \) and \( x = \dfrac{5}{2} \). These \( x \)-intercepts are the zeros of polynomial \( f(x) \). Because the graph crosses the \( x \)-axis at \( x = 0 \) and \( x = \dfrac{5}{2} \), both zeros have an odd multiplicity. The graph at \( x = 0 \) has a cubic shape and therefore the zero at \( x = 0 \) has multiplicity of 3. The shape of the graph at \( x = \dfrac{5}{2} \) is close to linear, hence the zero at \( x = \dfrac{5}{2} \) has multiplicity equal to 1. Using the zeros at \( x = 0 \) and \( x = \dfrac{5}{2} \), \( f(x) \) may be written as
\[ f(x) = k(x - 0)^3 \left(x - \dfrac{5}{2}\right), \quad \text{where } k \text{ is a constant.} \]We now use the point \( (2, -4) \) to find \( k \).
\[ -4 = k(2)^3 \left(2 - \dfrac{5}{2}\right), \quad \text{solve for } k \text{ to obtain} \quad k = 1 \]The equation of polynomial \( f(x) \) is given by
\[ f(x) = x^3 \left(x - \dfrac{5}{2}\right) \]Question 4 - Cubic Polynomial Coefficients
The graph of a cubic polynomial \( y = a x^3 + b x^2 +c x + d \) is shown below. Find the coefficients \( a, b, c \) and \( d \).
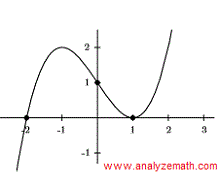
The polynomial has degree 3. The graph of the polynomial has a zero of multiplicity 1 at \( x = -2 \) which corresponds to the factor \( x + 2 \), and a zero of multiplicity 2 at \( x = 1 \) which corresponds to the factor \( (x - 1)^2 \). Hence the polynomial may be written as
\[ y = k(x + 2)(x - 1)^2 \]We now need to find \( k \) using the y-intercept \( (0 , 1) \) shown in the graph.
\[ 1 = k(0 + 2)(0 - 1)^2 = 2k \]Solve for \( k \).
\[ k = \dfrac{1}{2} \]We now expand the polynomial, write it in standard form and identify the coefficients \( a \), \( b \), \( c \), and \( d \).
\[ y = \dfrac{1}{2}(x + 2)(x - 1)^2 = 0.5x^3 - 1.5x + 1 \]We now compare the expression of the polynomial found above to
\[ y = ax^3 + bx^2 + cx + d \]and obtain the values of the coefficients
\[ a = 0.5, \quad b = 0, \quad c = -1.5, \quad d = 1 \]Question 5 - Even Polynomial Symmetry
The graph of polynomial \( y=a x^4+bx^3+c x^2+d x+e \) is symmetric with respect to the y-axis as shown below. Find the coefficients \( b, d \) and \( e \).
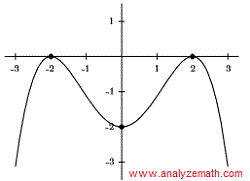
The graph of the polynomial is symmetric with respect to the y-axis and therefore the polynomial function given above must be an even function. The terms \( b x^3 \) and \( d x \) included in the given expression of the polynomial above are not even and therefore their coefficients are equal to 0. Hence
\[ b = 0 , \quad d = 0 \]and therefore \( y \) is given by
\[ y = a x^4 + c x^2 + e \]Coefficient \( e \) is found using the y-intercept \( (0 , -2) \) from the graph.
\[ -2 = a (0)^4 + c (0)^2 + e \] \[ e = -2 \]