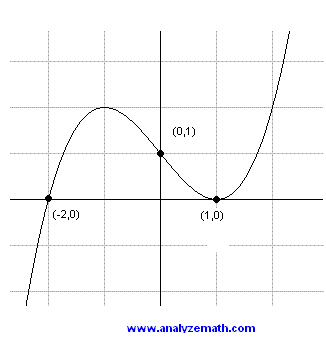
Problem 1:
The graph of a cubic polynomial

.

Solution to Problem 1:

• This polynomial has a zero of multiplicity 1 at x = -2 and a zero of multiplicity 2 at x = 1. Hence the polynomial may be written as
  y = a (x + 2)(x - 1) ²
  
• This polynomial has a y intercept (0 , 1). Hence
  1 = a (0 + 2)(0 - 1) ²
  
• Solve for a to obtain
  a = 1 / 2
  
• The polynomial may now be written as follows
  y = (1 / 2) (x + 2)(x - 1) ²
  
• Expand to obtain
  y = (1 / 2) x ³ -(3 / 2) x + 1
  
• We now identify the coefficients as follows
  a = 1/2 , b = 0, c = -3/2 and d = 1

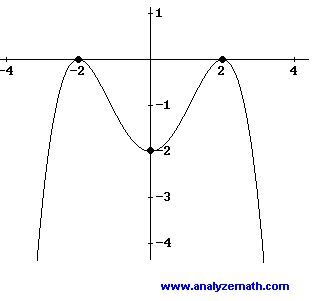
Problem 2:
The graph of the polynomial

.

Solution to Problem 2:

• This polynomial has a zero of multiplicity 2 at x = - 2 and a zero of multiplicity 2 at x = 2. Hence it may be written as
  y = a (x + 2) ² (x - 2) ²
  
• We now use the y intercept at (0 , -2) to write the equation
  -2 = a (0 + 2) ² (0 - 2) ²
  
• Solve the above for a to obtain
  a = - 1 / 8
  
• We now write the polynomial as follows
  y = (-1 / 8) (x + 2) ² (x - 2) ²
  
• Expand
  y = (-1 / 8) x ⁴ + x ² - 2
  
• We now identify the coefficients
  a = -1 / 8, b = 0, c = 1, d = 0, e = -2

Problem 3:
The polynomial

Solution to Problem 3:

• If f has a zero of multiplicity 2, then it may be written as follows
  f(x) = (x + 2) ² Q(x)
  
• Where Q(x) is a polynomial of degree 4 and may be found by division
  Q(x) = f(x) / (x + 2) ² = x ⁴ -3 x ² + 1
  
• Polynomial f may now be written as
  f(x) = (x + 2) ² (x ⁴ -3 x ² + 1)
  
• The remaining zeros of polynomial f may be found by solving the equation
  x ⁴ -3 x ² + 1 = 0
  
• It is an equation of the quadratic type with solutions
  ( √(5) + 1 ) / 2 , ( √(5) - 1 ) / 2 , ( - √(5) - 1 ) / 2 , ( - √(5) + 1 ) / 2

Problem 4:
The polynomial

Solution to Problem 4:

• polynomial f may be written as
  f(x) = (x + √(5)) (x - √(5)) Q(x) = (x ² - 5) Q(x)
  
• Q(x) may be found by division
  Q(x) = f(x) / (x ² - 5) = 3 x ² + 5 x - 2
  
• Hence f(x) may be written as
  f(x) = (x ² - 5) (3 x ² + 5 x - 2 )
  
• The remaining zeros may found by solving the equation
  3 x ² + 5 x - 2 = 0
  
• Solve the above equation to find the remaining zeros of f.
  -2 and 1 / 3

Problem 5:
A polynomial of degree 4 has a positive leading coefficient and simple zeros (i.e. zeros of multiplicity 1) at x = 2, x = - 2, x = 1 and x = -1. Is the y intercept of the graph of this polynomial positive or negative?

Solution to Problem 5:

• All polynomials with degree 4 and positive leading coefficient will have a graph that rises to the left and to the right. And since the polynomial has two negative zeros and two positive zeros, then the only possibility for the y intercept is to be positive.

Problem 6:
The graph of polynomial p is shown below.

.

Solution to Problem 6:

• a - odd
  
• b - negative
  
• c - No. The degree of a polynomial depends on the real and complex zeros. The graph shows only the real zeros. Hence, not enough information is given to find the degree of the polynomial.

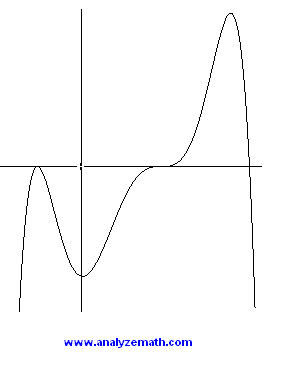
Problem 7:
Give 4 different reasons why the graph below cannot be the graph of the polynomial p give by.

.

Solution to Problem 7:

• 1 - The given polynomial has degree 4 and positive leading coefficient and the graph should rise on the left and right sides.
  
• 2 - p(0) = 1, graph shows negative value.
  
• 3 - the equation x ⁴ - x ² + 1 = 0 has no solution which suggests that the polynomial p(x) = x ⁴ - x ² + 1 has no zeros. The graph shows x intercepts.
  
• 4 - The graph has a zero of multiplicity 2, a zero of multiplicity 3 and and a zero of multiplicity 1. So the degree of the graphed polynomial should be at least 6. The given polynomial has degree 4.