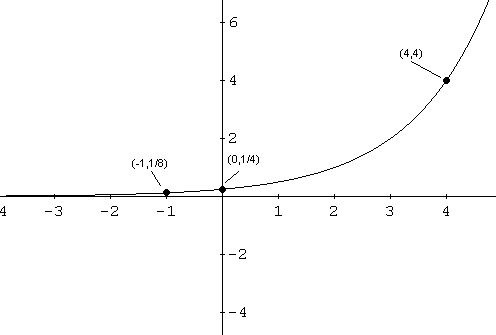| Revisione Per prima cosa si aprono con le propriet� del grafico della funzione esponenziale di base di base di uno, f (x) = a x , a > 0 e non uguale a 1. Il dominio della funzione f � l'insieme di tutti i numeri reali. La gamma di f � l'intervallo (0, + infinito). Il grafico di f ha un asintoto orizzontale dato da y = 0. Funzione f � intercettare ay a (0, 1). f � una funzione crescente, se uno � superiore a 1 e una funzione decrescente se a � minore di 1.
Si consiglia di rivedere tutte le propriet� di cui sopra della funzione esponenziale in modo interattivo.
Esempio 1: f � una funzione data da
f (x) = 2(x - 2) - Trovare il dominio e la gamma di f.
- Trovare l'asintoto orizzontale del grafico.
- Trova la x e intercetta y del grafico. di f se ce ne sono.
- Disegnare il grafico di f.
Risposta a Esempio 1 - Il dominio di f � l'insieme di tutti i numeri reali. Per trovare la gamma di f, si comincia con
Moltiplicare entrambi i lati da 2 -2 che � positivo. Utilizzare le propriet� esponenziale
Questa ultima affermazione suggerisce che f (x)> 0. La gamma di f � (0, + inf).
Come x diminuisce senza limite, f (x) = 2 (x - 2) si avvicina a 0. Il grafico di f ha un asintoto orizzontale in y = 0.
Per trovare l'intercetta x abbiamo bisogno di risolvere l'equazione
Questa equazione non ha ancora una soluzione, vedi gamma precedente, f (x)> 0. Il grafico di f non ha ancora una intercetta x. L'intercetta y � data da (0, f (0)) = (0,2 (0 - 2)) = (0, 1 / 4).
Fino ad ora abbiamo il dominio, la gamma, intercetta su y e l'asintoto orizzontale. Abbiamo bisogno di punti extra. (4, f (4)) = (4, 2 (4 - 2)) = (4, 2 2) = (4, 4)
(-1, F (-2)) = (-1, 2 (-1 - 2)) = (-1, 2 -3) = (-1, 1 / 8)
Ora ci permetta di utilizzare tutte le informazioni di cui sopra al grafico di f.
 Problema abbinate a Esempio1: f � una funzione data da
f (x) = 2(x+2)
- Trovare il dominio e la gamma di f.
- Trovare l'asintoto orizzontale del grafico di f.
- Trova la x e intercetta y del grafico di f se ce ne sono.
- Disegnare il grafico di f.
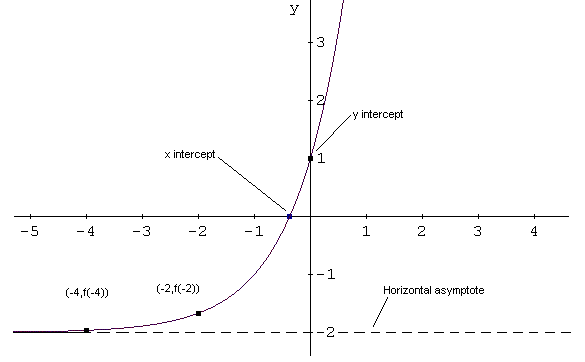
Esempio 2: f � una funzione data da f (x) = 3 (x + 1) - 2 - Trovare il dominio e la gamma di f.
- Trovare l'asintoto orizzontale del grafico di f.
- Trova la x e intercetta y del grafico di f se ce ne sono.
- Disegnare il grafico di f.
Risposta a Esempio 2 - Il dominio di f � l'insieme di tutti i numeri reali. Per trovare la gamma di f, si comincia con
Moltiplicare entrambi i lati da 3, che � positivo.
Utilizzare le propriet� esponenziale
Sottrarre 2 per entrambe le parti
Questa ultima affermazione suggerisce che f (x)> -2. La gamma di f � (-2, + inf).
- Come x diminuisce senza limite, f (x) = 3 (x + 1) -2 approcci -2. Il grafico di f ha un asintoto orizzontale y = -2.
- Per trovare l'intercetta x abbiamo bisogno di risolvere l'equazione f (x) = 0
Aggiungere 2 su entrambi i lati dell'equazione
Riscrivere l'equazione di cui sopra in forma logaritmica
Risolviamo per x
L'intercetta y � data da (0, f (0)) = (0,3 (0 + 1) - 2) = (0, 1).
- Fino ad ora abbiamo il dominio, gamma, X e Y e intercetta l'asintoto orizzontale. Abbiamo bisogno di punti extra.
(-2, F (-2)) = (-2, 3 (2 + 1) - 2) = (4, 1/3-2) = (4, -1,67)
(-4, F (-4)) = (-4, 3 (-4 + 1) - 2) = (-4, 2 -3) = (-4, -1,99)
Ora ci permetta di utilizzare tutte le informazioni di cui sopra al grafico di f.
Problema abbinate a Esempio2: f � una funzione data da
f (x) = 2 (x - 2) + 1
- Trovare il dominio e la gamma di f.
- Trovare l'asintoto orizzontale del grafico di f.
- Trova la x e intercetta y del grafico di f se ce ne sono.
- Disegnare il grafico di f.
Pi� riferimenti e link funzioni esponenziali e grafica.
|