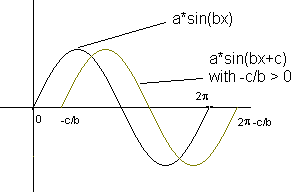| |
| Le propriet�, come dominio, gamma e intercetta i grafici di queste funzioni sono anche guardato in dettaglio. Revisione Per prima cosa comincia con il grafico della funzione di base sine f (x) = sin (x) Il dominio della funzione f � l'insieme di tutti i numeri reali. La gamma di f � l'intervallo [-1,1]. -1 <= Sin (x) <= 1 (<= significa minore o uguale) Anche la funzione f � periodica con periodo pari a 2 p. Il grafico di f su un periodo pu� essere abbozzata da trovare prima i punti che danno informazioni importanti, quali x intercetta, intercetta su y, massimi e minimi. Facciamo una tabella di valori per la funzione f sopra l'intervallo di un periodo di: [0, 2 p].
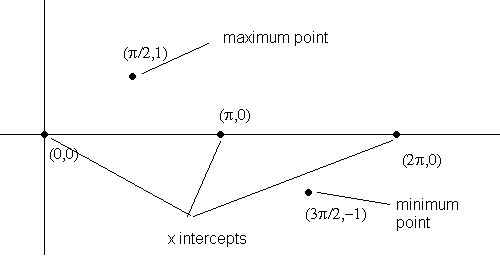
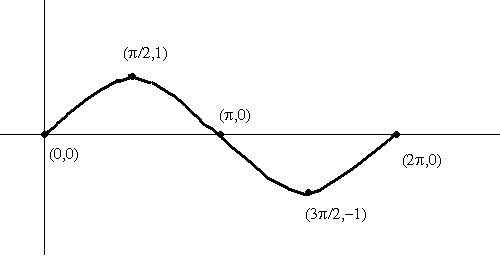
La scelta dei valori di x nella tabella corrispondono a X e Y intercettazioni, massimi e minimi punti. Questi sono i punti utili per rappresentare graficamente la funzione seno per un periodo di: [0, 2 p].Per rappresentare graficamente f, abbiamo primo grafico i punti della tabella si uniscono questi punti. Naturalmente � possibile aggiungere punti extra se lo si desidera.� Ma i cinque punti utilizzati sono i punti chiave.� Un altro punto importante da notare � che i 5 punti chiave di suddividere il periodo in 4 parti uguali. Figura sotto.
�
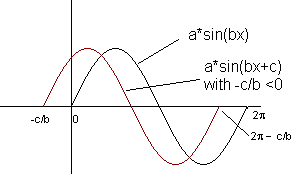
Per avere un quadro completo del motivo per cui il grafico del peccato (x) cambiamenti con x come sopra indicato, si consiglia di passare attraverso un tutorial interattivo sulla circonferenza trigonometrica unit� cerchio unitario trigonometriche. Grafica f (x) = a * sin (bx + c) Dobbiamo prima capire come fare i parametri a, b, c incidere il grafico di f (x) = a * sin (bx + c) se confrontato con il grafico di sin (x)? Si consiglia di passare attraverso un tutorial interattivo su funzioni seno. Il dominio di f � l'insieme di tutti i numeri reali. La gamma di espressione bx + c � l'insieme di tutti i numeri reali. Pertanto, la gamma del peccato (bx + c), � [-1,1]. Quindi -1 <= sin (bx + c) <= 1 Moltiplicare entrambi i lati da A. Se a> 0 -a <= a * (bx + c) <= a Se a <0 (simboli di cambiamento di disuguaglianza) -a> = a*sin (bx + c)> = a a<= a*sin (bx + c) <= - a � Possiamo dire che il parametro di un effetto della gamma di f, che pu� essere scritta come [- | a |, | a |]. | A | si chiama l'ampiezza. Periodo di f Cominciamo col supporre che c = 0 e f (x) = a * sin (bx). Per f per completare un ciclo (periodo), bx espressione deve variare da 0 a 2 p. 0 <= bx <= 2 p. Dividere tutti i termini della disuguaglianza di B. Se b> 0 0 <= x <= 2 p / b. Periodo 2 p / b - 0 = 2 p / b. Se b <0 (simboli di cambiamento di disuguaglianze) 0> = x> = 2 p / b. Che � equivalente a 2 p / b <= x <= 0. Periodo = 0 - 2 p / b = - 2 p / b Utilizzando la notazione di valore assoluto si pu� scrivere il periodo di f = 2 p / | b |. Phase Shift Consideriamo ora l'intero argomento bx + c. Per F per completare un ciclo (periodo), espressione bx + c deve variare da 0 a 2 p. 0 <= bx + c <= 2 p. Assumere b> 0 e risolvere per x -c <= bx <= 2 p-c. -c / b <= x <= 2 p / b - c / b. Periodo di f = 2 p / b - c / b - (-c / b) = 2 p / | b |. c non pregiudica il periodo. Vediamo ora confrontare il ciclo [0, 2 p / b] quando c = 0 con il ciclo [-c / b, 2 p / b - c / b]. Questo indica che vi � uno spostamento di-c / b. -c / b si chiama sfasamento. Se-c / b <0, il passaggio sar� quello di sinistra. Se-c / b> 0, il passaggio sar� quello di destra.
Esempio 1: f � una funzione data da f (x) = 2sin (3x - p / 2) � a - Trovare il dominio di f e la gamma di f. b - Trova il periodo e lo sfasamento del grafico di f. c - Disegna il grafico della funzione f su un periodo. Risposta a Esempio 1 a - Il dominio di f � l'insieme di tutti i numeri reali. La gamma � data da l'intervallo [-2, 2]. b - Periodo = 2 p / | b | = 2 p / 3 Sfasamento = - c / b = - (- p / 2) / 3 = p / 6 c - per tracciare il grafico di f su un periodo, abbiamo bisogno di trovare i 5 punti chiave per primo. Let 3x - p / 2 varia da 0 a 2 p in modo da avere un periodo di completa poi trovare i valori di f (x).Si veda la tabella qui sotto.
Ora dobbiamo trovare i corrispondenti valori di x. La prima riga della tabella di cui sopra d� 0 <= 3x - p / 2 <= 2 p Risolviamo per x p / 2 <= 3x <= 2 p + p / 2 p / 2 <= 3x <= 5p / 2 p / 6 <= x <= 5p / 6 Ora completare la tabella con i valori x. Una volta che i valori x P / 6 e 5p / 6 che descrive un intero periodo si trovano, gli altri 3 punti si trovano come segue: Il valore medio = (p / 6 + 5p / 6) / 2 = 3p / 6 Valore al primo trimestre = (p / 6 + 3p / 6) / 2 = 2p / 6 Valore al terzo trimestre = (3p / 6 + 5p / 6) / 2 = 4p / 6 Le frazioni non sono state ridotte, questo render� pi� facile scalare l'asse x in unit� di p / 6 e grafico dei punti.
Ora mettere i punti dati (x, f (x)) e di unirsi a loro da una curva regolare.
� Abbinate Problema: f � una funzione data da f (x) = (1 / 2) sin (4x + p / 2) � a - Trovare il dominio di f e la gamma di f. b - Trova il periodo e lo sfasamento del grafico di f. c - Disegna il grafico della funzione f su un periodo. Pi� riferimenti e link a grafica, grafici di funzioni e funzioni seno. |