In ci� che segue, SQRT significa radice quadrata.
Il dominio della funzione f definita da f (x) = SQRT (x) � l'insieme di tutti i numeri reali positivi e pari a zero, perch� la radice quadrata di numeri negativi, non sono numeri reali (si pensi SQRT (- 4), is it real? ). In forma disuguaglianza, il dominio di f (x) = SQRT (x) � scritto come
x >= 0
in forma di intervallo, il dominio � dato da
[0, + infinito)
Esempio 1: Grafico
f (x) = SQRT (x)
e trovare la gamma di f. Soluzione Esempio 1:
Perch� il dominio di f � l'insieme di tutti i numeri reali positivi e pari a zero, si potrebbe costruire una tabella di valori come segue:
| x | 0 | 1. | 4 | 9 | 16 |
| SQRT (x) | 0 | 1. | 2 |
3 |
4 |
I valori di x sono stati selezionati in modo che la radice quadrata di questi valori sono numeri interi che rendono facile tracciare i punti riportati nella tabella.
La gamma di f � dato da l'intervallo [0, + infinito).
Esempio 2: Grafico
f (x) = SQRT (x - 3)
e trovare la gamma di f. Soluzione Esempio 2:
Primo a trovare il dominio della funzione radice quadrata di cui sopra, affermando che l'espressione sotto la radice quadrata deve essere positivo o uguale a zero
x - 3> = 0
Risolvere le disuguaglianze di cui sopra per ottenere il dominio di f come l'insieme di tutti i valori reali tale che
x> = 3
Ora selezionare i valori di x nel dominio di costruire una tabella di valori.
| x | 3 | 4 | {0 | 12 |
| SQRT (x - 3) | 0 | 1. | 2 |
3 |
L'intervallo [0, + infinito) rappresenta l'intervallo di f.
Esempio 3: Grafico
f (x) = - SQRT (- 2x + 4) + 1
e trovare la gamma di f. Soluzione Esempio 3:
Il dominio della funzione di cui sopra si trova impostando
- 2x + 4> = 0
Risolvere le disuguaglianze di cui sopra per ottenere il dominio di f come l'insieme di tutti i valori reali tale che
x <= 2
Ora selezionare i valori di x nel dominio di f per costruire una tabella di valori. Questi valori sono scelti in modo che la radice quadrata termine � un numero intero e dare i punti che sono facili da tracciare.
| x | 2 | 3 / 2 | 0 | -5 / 2 | -6 |
| - SQRT (-2 x + 4) + 1 | 1. | 0 | -1 |
-2 |
-3 |
La gamma di f � dato da l'intervallo (-infinito, 1].
Esempio 4: Grafico
f (x) = SQRT (- x 2 + 4)
e trovare la gamma di f. Soluzione Esempio 4:
Il dominio della funzione di cui sopra si trova risolvendo il polinomio disuguaglianza
- x2 + 4 >= 0
La soluzione insieme di disuguaglianza di cui sopra � data da l'intervallo
[-2 , 2]
che � anche il dominio della funzione di cui sopra.
Scriviamo la funzione data come un'equazione come segue
y = SQRT (- x 2 + 4)
Quadrato entrambi i lati e procura.
x 2 + y 2 = 22
L'equazione ottenuta � quella di un cerchio. Quindi il grafico di f (x) = SQRT (- x 2 + 4) � la met� superiore di un cerchio sinsce SQRT (- x 2 + 4) � positivo. Quindi il grafico qui sotto.
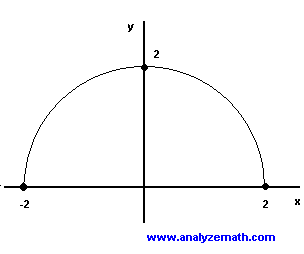L'intervallo [0, 2] rappresenta l'intervallo di f.
Esempio 5: Grafico
f (x) = SQRT (x 2 - 9)
e trovare la gamma di f. Soluzione Esempio 5:
Il dominio della funzione di cui sopra si trova risolvendo
x 2 - 9> = 0
Che d� un dominio reprsented da
(-infinito, -3] U [3, + infinito)
Ora selezionare i valori di x nel dominio di f per costruire una tabella di valori, rilevando f (x) = f (-x) quindi una simmetria del grafico rispetto all'asse y.
| x | 3 | 5{/0 | 8 |
| SQRT (x 2 - 9) | 0 | 4 | 7,4 |
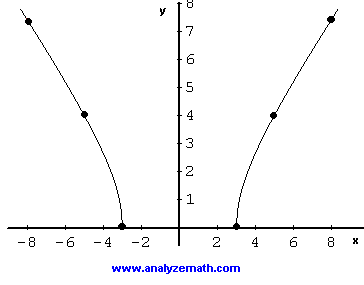
La gamma di f � dato da l'intervallo [0, + infinito).
Esempio 6: Grafico
f (x) = SQRT (x 2 - 6x + 9)
e trovare la gamma di f. Soluzione Esempio 6:
Usiamo scrivere l'espressione sotto la radice quadrata di un quadrato come segue
x 2 - 6x + 9 = (x - 3) 2
Quindi
f (x) = SQRT (x 2 - 6x + 9)
= SQRT ((x - 3) 2) = | x - 3 |
La funzione data � stata rewitten come una funzione di assoluto valore. Funzione f pu� essere scritta come una funzione a tratti e rappresentati graficamente come segue.
La gamma di f � dato da l'intervallo [0, + infinito).
Esempio 7: Grafico
f (x) = SQRT (x 2 + 4x + 6)
e trovare la gamma di f. Soluzione Esempio 7:
Utilizzare completando il quadrato di rewtite l'espressione sotto la radice quadrata come segue
x 2 + 4x + 6 = (x + 2) 2 + 2
L'espressione sotto la radice quadrata � sempre positivo quindi il dominio di f � l'insieme di tutti i numeri reali. Vediamo prima guardare il grafico di (x + 2) 2 + 2. Si tratta di una parabola.
Ci aspetteremmo che il grafico di f ad avere lo stesso asse di simmetria, la linea verticale, x = -2 come mostra il grafico di cui sopra. La tabella di valori pu� costruito nel modo seguente.
| x | 2. | 0 | 2 | 4 |
| SQRT ((x + 2) 2 + 2) | 1,4 | 2,4 | 4,2 |
6,2 |
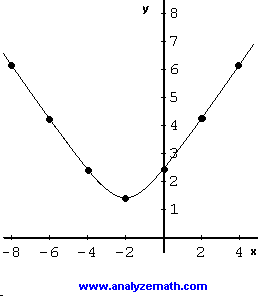
La gamma di f � dato da l'intervallo [SQRT (2), + infinito).
Pi� riferimenti e link a grafica.
Graphing Funzioni
|
