| |
| Alcune delle propriet� del grafico di f (x) = tan (x) sono i seguenti: Esempio 1: Grafico Pi� di un periodo. Soluzione Esempio 1:
Notiamo che per x che tende pi / 2 da sinistra (per valori inferiori a pi / 2) tan x aumenta undefinetely. Diciamo che il grafico di tan x � un asintoto per x = pi / 2. Esso � rappresentato da una linea spezzata rossa verticale x = pi / 2 nel grafico qui sotto. Ora guardiamo i valori di tan x per x vicino a-pi / 2 tali che x � pi� grande poi-pi / 2.
Notiamo che per x che tende-pi / 2 da destra (per valori superiori a-pi / 2) tan x diminuisce undefinetely. Il grafico di tan x � un asintoto per x =-pi / 2. Esso � rappresentato da una linea spezzata rossa verticale x =-pi / 2 nel grafico qui sotto. tan x ha un comportamento asintotico vicino a pi / 2 e-pi / 2. Utilizzando i valori di tan x sopra, pi� i seguenti valori: tan 0 = 0, pi tan / 4 = 1 e tan-pi / 4 = -1, Iniziamo riportando i punti (0,0), (pi / 4,1) e (-pi / 4, -1) e gli asintoti verticali.  Abbiamo quindi disegnare una curva regolare che passa dai punti di calcolo. Vicino alla asintoti verticali, il grafico va verso l'alto o undefinetely (vicino a x = pi / 2 asintoto verticale) e verso il basso undefinetely (vicino a x =-pi / 2 asintoto verticale).  Fase 1: Creare una tabella di valori per un periodo.
Fase 2: Rappresentare i punti e gli asintoti verticali. Fase 3: Disegna una curva che passa attraverso tutti i punti e sale o scende verticalmente lungo la asintoti verticali. Esempio 2: Grafico funzione f data da Pi� di un periodo. Soluzione Esempio 2:
Adesso noi usiamo la relazione tra x e t, t = 2 x - pi / 4, per trovare i valori di x corrispondenti a valori di t utilizzato nella tabella di cui sopra. Solve t = 2 x - pi / 4 per x. x = t / 2 + pi / 8 Una riga che mostra i valori di x pu� essere aggiunto alla tabella di cui sopra: Questi valori di x sono stati trovati con x = t / 2 + pi / 8 trovati sopra ed i valori di t nella tabella.
Ora abbiamo i valori della funzione di 2 t tan ed i corrispondenti valori x. Abbiamo informazioni sufficienti per rappresentare graficamente la funzione data.  Esempio 3: Grafico funzione f definita da Pi� di un periodo. Soluzione Esempio 3:
Solve t = x + pi / 2 per X. x = t - pi / 2 Una riga che mostra i valori di x viene aggiunto alla tabella di cui sopra.
Ora abbiamo i valori della funzione - t tan ed i corrispondenti valori x. 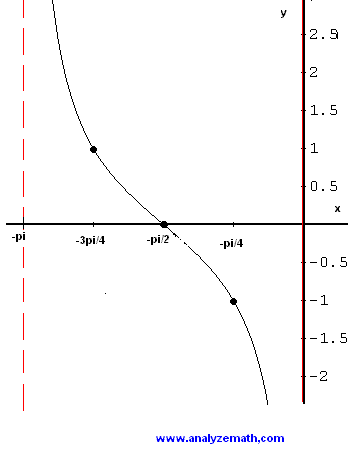 Pi� riferimenti e link a grafica. Graphing Funzioni Funzione tangente. Tangente la funzione f (x) = a tan (bx + c) + d e le sue propriet�, come grafico, periodo, sfasamento e asintoti sono esplorate in modo interattivo, modificando i parametri a, b, c, d utilizzando un applet + + + |