Add, Subtract and Scalar Multiply Matrices
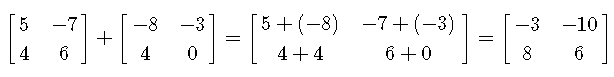
Operations on Matrices such as adding, subtracting and multiplying by a scalar along with the equality of matrices are presented using examples and questions with solutions.
Page Content
- Add and Subtract Matrices
- Multiply a Matrix by a Scalar
- Equality of two Matrices
- Questions on Matrices
- Solutions to the Questions
- References
Add and Subtract Matrices
Only matrices
of the same order can be added or subtracted. We add (or subtract) two matrices by adding (or subtracting) their corresponding entries.
Example 1
Rewrite, if possible, each of the following expressions as a single matrix.
Solution
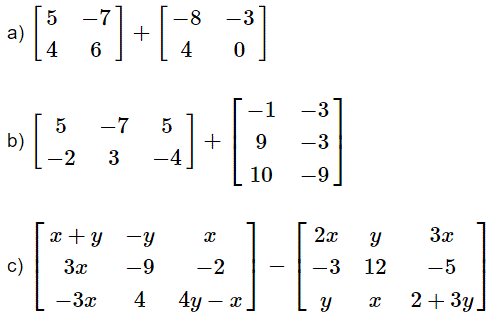
a) The matrices in part a) have the same order and we therefore can add them by adding their corresponding entries. Hence
b) The matrices in part b) do not have the same order and we therefore cannot add them.
c) The matrices in part c) have the same order and we therefore can add them by adding their corresponding entries and simplifying the algebraic expressions.
Multiply a Matrix by a Scalar
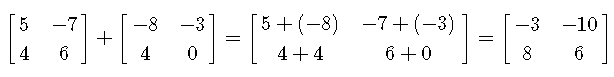
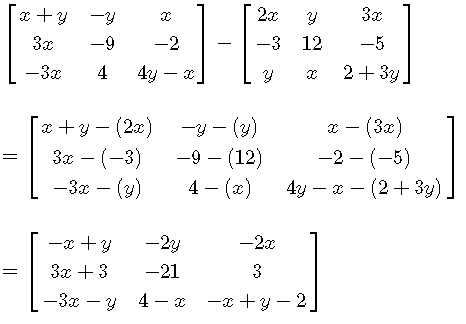
To multiply a matrix by a scalar, you multiply all entries of that matrix by the scalar. Note that scalar multiplication does not change the order of the matrix.
\( \)\( \)\( \)\( \)
Example 2
Express as a single matrix.
a) - 5 \( \begin{bmatrix} 5 & - 7 \\ 4 & 6 \end{bmatrix} \)
b) \( 2 \begin{bmatrix} x & x + y & 6\\ -2 & - x & 1 \end{bmatrix} - 3 \begin{bmatrix} - x & -2y & 0\\ 3x & x & -1 \end{bmatrix} \)
Solution
a) - 5 \( \begin{bmatrix} 5 & - 7 \\ 4 & 6 \end{bmatrix} = \begin{bmatrix} -5(5) & -5(- 7) \\ -5(4) & -5(6) \end{bmatrix}= \begin{bmatrix} -25 & 35 \\ -20 & - 30 \end{bmatrix}\)
b) \( 2 \begin{bmatrix} x & x + y & 6\\ -2 & - x & 1 \end{bmatrix} - 3 \begin{bmatrix} - x & -2y & 0\\ 3x & x & -1 \end{bmatrix} \)
Multiply the first matrix by 2 and the second matrix by 3
\( = \begin{bmatrix} 2(x) & 2(x + y) & 2(6)\\ 2(-2) & 2(- x) & 2(1) \end{bmatrix} - \begin{bmatrix} 3(-x) & 3(-2y) & 3(0)\\ 3(3x) & 3(x) & 3(-1) \end{bmatrix} = \)
Subtract, group and simplify the algebraic expressions
\( = \begin{bmatrix} 5x & 2x+8y & 12\\ -4 - 9x & -5x & 5 \end{bmatrix}\)
Equality of two Matrices
Two matrices are equal if they have the same order (equal number of rows and equal number of columns) and their corresponding entries are equal.
Example 3
Which of the following matrices are equal?a) \( \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix} \), b) \( \begin{bmatrix} x & 2x \\ 2 & 1 \\ \end{bmatrix} \), c) \( \begin{bmatrix} 1 & -x \\ 3x & 5 \\ \end{bmatrix} \), d) \( \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix} \), e) \( \begin{bmatrix} 1 & 2 & 5\\ 3 & 4 & 8\\ \end{bmatrix} \),
Solution
Matrices a), b), c) and d) have the same order 2 by 2. But only matrices a) and d) are equal as they have equal corresponding entries. Matrix e) has the order 2 by 3 which is different to the order of all other matrices and is therefore not equal to any of the matrices.
Example 4
Find x and y so that \[ \begin{bmatrix} 2x + y & - 7 \\ 4 & 6 \end{bmatrix} = \begin{bmatrix} 2 & - 7 \\ 4 & 4x + y \end{bmatrix} \].
Solution
The two matrices have the same order. For these matrices to be equal, all their corresponding entries have to be equal. Corresponding entries - 7 and 4 are equal. The entries with the unknowns x and y has to be equal. Hence
2 x + y = 2 and 6 = 4 x + y
Solve the above system of equations to find
x = 2 , y = - 2
As an exercise, substitute x by 2 and y by - 2 into the matrices and verify that they are equal.
Questions on Matrices
-
Part 1
Find x and y, if possible, such that
A) \( \begin{bmatrix} 2x + y & 3 & 10 \\ y + 1 & -2 & 0 \\ \end{bmatrix} = \begin{bmatrix} 2 & 3 & 10 \\ 3 & -2 & 0 \\ \end{bmatrix} \)
B) \( \begin{bmatrix} 6 & -4 & -6 & x - y \end{bmatrix} = - 2 \begin{bmatrix} -3 & 2 & 2x + 2y & 13 \end{bmatrix} \) -
Part 2
Write as one matrix
A) \( \begin{bmatrix} -2 & 4 & 3 \\ -6 & 3 & -4 \\ -1 & 0 & 9 \\ \end{bmatrix} + \begin{bmatrix} -1 & 0 & 23 \\ -4 & -3 & 9 \\ 2 & -5 & 0 \\ \end{bmatrix} \)
B) \( - 2 \begin{bmatrix} -2 & 3 \\ 1 & -5 \end{bmatrix} + 4 \begin{bmatrix} 3 & 4 \\ -2 & 9 \end{bmatrix} \)
C) \( -3 \begin{bmatrix} -2x & y + 2 & 6\\ 4 & - x & -4 \\ \end{bmatrix} + 5 \begin{bmatrix} 3x & 5y & -5\\ 3y & x+y & -1 \end{bmatrix} \)
Solutions to the Questions
-
Part 1
A) The two matrices have the same order and to be equal, they need to have equal corresponding entries. Hence the simultaneous equations. 2x + y = 2 and y + 1 = 3
Solve the above equations to obtain: x = 0 and y = 2.
B) Multiply the second equation by -2 and rewrite the given equation as follows: \( \begin{bmatrix} 6 & -4 & -6 & x - y \end{bmatrix} = \begin{bmatrix} 6 & -4 & -2(2x + 2y) & -26 \end{bmatrix}\)
For the two equations to be equal, we need to have
-2(2x + 2y) = - 6 and x - y = - 26
Solve the above system to obtain: x = -49/4 and y = 55/4 -
Part 2
A) \( \begin{bmatrix} -2 & 4 & 3 \\ -6 & 3 & -4 \\ -1 & 0 & 9 \end{bmatrix} + \begin{bmatrix} -1 & 0 & 23 \\ -4 & -3 & 9 \\ 2 & -5 & 0 \end{bmatrix} = \begin{bmatrix}-3&4&26\\ -10&0&5\\ 1&-5&9\end{bmatrix} \)
B) \( - 2 \begin{bmatrix} -2 & 3 \\ 1 & -5 \end{bmatrix} + 4 \begin{bmatrix} 3 & 4 \\ -2 & 9 \end{bmatrix} = \begin{bmatrix}16&10\\ -10&46\end{bmatrix}\)
C) \( -3 \begin{bmatrix} -2x & y + 2 & 6\\ 4 & - x & -4 \end{bmatrix} + 5 \begin{bmatrix} 3x & 5y & -5\\ 3y & x+y & -1 \end{bmatrix} = \begin{bmatrix}21x&22y-6&-43\\ -12+15y&8x+5y&7\end{bmatrix}\)
