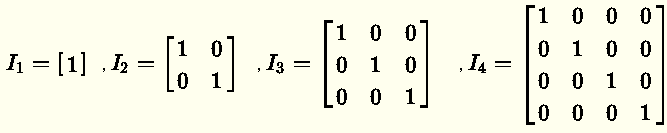Identity Matrix

Identity matrices are presented along with their properties including examples and exercises with detailed solutions.

Definition of the Identity Matrix

An identity matrix is a square matrix with all diagonal entries equal to \( 1 \) and all other entries equal to zero.

These are examples of identity matrices of dimensions \( 1 \times 1 \), \( 2 \times 2 \), \( 3 \times 3 \), \( 4 \times 4 \), …

\[ I_1 = [1] \quad , \quad I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \quad , \quad I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \quad , \quad I_4 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

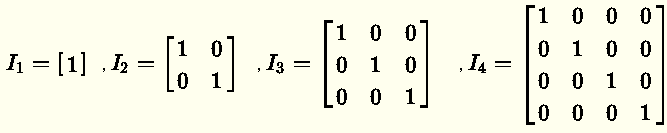
One of the most important properties of identity matrices is that the product of a square matrix \( A \) of dimension \( n \times n \) with the identity matrix \( I_n \) equals \( A \):

\( A I_n = I_n A = A \)

The identity matrix is used to define the inverse of a matrix. Matrices \( A \) and \( B \), of dimensions \( n \times n \), are inverses of each other if:

\( A B = B A = I_n \)

Properties of the Identity Matrix

In what follows, \( A \) is a square matrix of dimension \( n \times n \). Some of the most important properties of identity matrices are given below.

  1. Multiplicative identity: the product of \( I_n \) by \( A \) equals \( A \).

    \( A I_n = I_n A = A \)

  2. Idempotent power: the product of \( k \) copies of \( I_n \) is \( I_n \) for every positive integer \( k \).

    \( I_n^k = I_n, \quad k \in \mathbb{Z}^{+} \)

  3. Inverse relationship: the product of \( A \) by its inverse \( A^{-1} \) equals \( I_n \).

    \( A A^{-1} = A^{-1} A = I_n \)

  4. Self-inverse: the inverse of \( I_n \) is \( I_n \).

    \( I_n^{-1} = I_n \)

  5. Symmetric / self-transpose: the transpose of \( I_n \) is \( I_n \).

    \( I_n^{T} = I_n \)

  6. Orthogonal matrix: \( I_n \) is an orthogonal matrix — its columns (and rows) form an orthonormal set, and:

    \( I_n^{T} I_n = I_n I_n^{T} = I_n \)

  7. Determinant: the determinant of \( I_n \) equals \( 1 \).

    \( \det(I_n) = 1 \)

Examples with Solutions

Example 1

Find \( x \), \( y \), \( z \), and \( w \) such that: \[ \begin{bmatrix} x-2 & y+1 \\ 2z-1 & w-2 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 6 \\ 9 & 10 \end{bmatrix} \]

Solution

The product on the left is of the form \( A I_2 \). By property 1, \( A I_2 = A \). Hence: \[ \begin{bmatrix} x-2 & y+1 \\ 2z-1 & w-2 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} x-2 & y+1 \\ 2z-1 & w-2 \end{bmatrix} \] Equating this to the right-hand side: \[ \begin{bmatrix} x-2 & y+1 \\ 2z-1 & w-2 \end{bmatrix} = \begin{bmatrix} 2 & 6 \\ 9 & 10 \end{bmatrix} \] Since two matrices of the same size are equal iff their corresponding entries are equal, we obtain the system: \[ x - 2 = 2, \quad y + 1 = 6, \quad 2z - 1 = 9, \quad w - 2 = 10 \] Solving each equation: \[ x = 4, \quad y = 5, \quad z = 5, \quad w = 12 \]

Answer: \( x = 4,\; y = 5,\; z = 5,\; w = 12 \).

Example 2

Simplify the expression \( A^{-1}(A + I_n) - I_n \), where \( A \) is a square matrix of dimension \( n \times n \).

Solution

Distribute \( A^{-1} \) over the sum: \[ A^{-1}(A + I_n) - I_n = A^{-1}A + A^{-1}I_n - I_n \] Apply property 3 (\( A^{-1}A = I_n \)) and property 1 (\( A^{-1}I_n = A^{-1} \)): \[ = I_n + A^{-1} - I_n \] Cancel \( I_n - I_n \): \[ = A^{-1} \]

Answer: \( A^{-1}(A + I_n) - I_n = A^{-1} \).

Example 3

Find matrix \( B \) and its inverse \( B^{-1} \) given \( A = \begin{bmatrix} 5 & 2 \\ 7 & 3 \end{bmatrix} \), \( B = \begin{bmatrix} 3 & x \\ y & 5 \end{bmatrix} \), and \( A B = I_2 \).

Solution

Substitute \( A \), \( B \), and \( I_2 \) into \( A B = I_2 \): \[ \begin{bmatrix} 5 & 2 \\ 7 & 3 \end{bmatrix} \begin{bmatrix} 3 & x \\ y & 5 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \] Multiply the matrices on the left: \[ \begin{bmatrix} 15 + 2y & 5x + 10 \\ 21 + 3y & 7x + 15 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \] Equating corresponding entries yields: \[ 15 + 2y = 1, \quad 5x + 10 = 0, \quad 21 + 3y = 0, \quad 7x + 15 = 1 \] From \( 15 + 2y = 1 \): \( 2y = -14 \Rightarrow y = -7 \), which also satisfies \( 21 + 3y = 0 \). From \( 5x + 10 = 0 \): \( x = -2 \), which also satisfies \( 7x + 15 = 1 \).

Thus: \[ B = \begin{bmatrix} 3 & -2 \\ -7 & 5 \end{bmatrix} \]

Verification. Compute \( B A \): \[ \begin{bmatrix} 3 & -2 \\ -7 & 5 \end{bmatrix} \begin{bmatrix} 5 & 2 \\ 7 & 3 \end{bmatrix} = \begin{bmatrix} 15 - 14 & 6 - 6 \\ -35 + 35 & -14 + 15 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I_2 \] Since \( A B = B A = I_2 \), the matrices \( A \) and \( B \) are inverses of each other, so \( B^{-1} = A \).

Answer: \( B = \begin{bmatrix} 3 & -2 \\ -7 & 5 \end{bmatrix} \) and \( B^{-1} = A = \begin{bmatrix} 5 & 2 \\ 7 & 3 \end{bmatrix} \).

Questions (with solutions below)

In what follows, \( A \), \( B \), and \( C \) are square matrices of dimension \( n \times n \).

  1. Part 1
    Matrices \( A \) and \( B \) are square matrices such that \( A B = I_n \). Find the product \( B^{-1} A^{-1} \).
  2. Part 2
    Find \( a \) and \( b \) such that: \[ \begin{bmatrix} 2 & 3 \\ a b & a + b \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 3 \\ 10 & 7 \end{bmatrix} \]
  3. Part 3
    Simplify the expression \( -A (A^{-1} + I_n) + I_n \).
  4. Part 4
    Given that \( B A = C \), write \( (B - A^{-1})(B^{-1} + A) \) in terms of \( C \) and \( C^{-1} \).

Solutions to the Above Questions

  1. Part 1
    Take the inverse of both sides of \( A B = I_n \): \[ (A B)^{-1} = I_n^{-1} \] Use \( (A B)^{-1} = B^{-1} A^{-1} \) and \( I_n^{-1} = I_n \): \[ B^{-1} A^{-1} = I_n \]
  2. Part 2
    Since multiplying by \( I_2 \) leaves a matrix unchanged: \[ \begin{bmatrix} 2 & 3 \\ a b & a + b \end{bmatrix} = \begin{bmatrix} 2 & 3 \\ 10 & 7 \end{bmatrix} \] Equating entries: \[ a b = 10 \quad \text{and} \quad a + b = 7 \] From \( a + b = 7 \), \( b = 7 - a \). Substitute into \( a b = 10 \): \[ a(7 - a) = 10 \implies a^2 - 7a + 10 = 0 \implies (a - 2)(a - 5) = 0 \] Thus \( a = 2 \) or \( a = 5 \), giving two ordered pairs: \[ (a, b) = (2, 5) \quad \text{or} \quad (a, b) = (5, 2) \]
  3. Part 3
    Distribute \( -A \): \[ -A (A^{-1} + I_n) + I_n = -A A^{-1} - A I_n + I_n \] Apply \( A A^{-1} = I_n \) and \( A I_n = A \): \[ = -I_n - A + I_n = -A \]
  4. Part 4
    Expand the product: \[ (B - A^{-1})(B^{-1} + A) = B B^{-1} + B A - A^{-1} B^{-1} - A^{-1} A \] Apply \( B B^{-1} = I_n \) and \( A^{-1} A = I_n \): \[ = I_n + B A - A^{-1} B^{-1} - I_n = B A - A^{-1} B^{-1} \] Using \( B A = C \) and \( (B A)^{-1} = A^{-1} B^{-1} = C^{-1} \): \[ = C - C^{-1} \]

More References and Links

  1. Linear Algebra – Questions with Solutions
  2. Matrices with Examples and Questions with Solutions
  3. Determinant of a Square Matrix
  4. Inverse Matrix Questions with Solutions
  5. Transpose of a Matrix
  6. Orthogonal Matrix
  7. Orthonormal Basis
  8. Howard Anton and Chris Rorres – Elementary Linear Algebra – 7th Edition
  9. Gilbert Strang – Introduction to Linear Algebra – 5th Edition (2016)
  10. Sheldon Axler – Linear Algebra Done Right – 3rd Edition (2015)
  11. Gareth Williams – Linear Algebra with Applications (2012)