Let us consider the following equations:
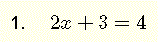this equation involves sums of real expressions and multiplications by real numbers
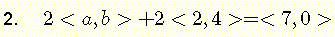this equation involves sums of 2-d vectors and multiplications by real numbers
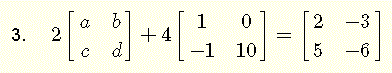this equation involves sums of 2 by 2 matrices and multiplications by real numbers
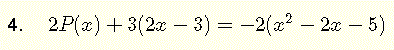this equation involves sums of polynommials and multiplications by real numbers.
It is obvious that if the set of real numbers in equation (1), the set of 2-d vectors used in equation (2), the set of the 2 by 2 matrices used in equation (3) and the set of polynomial used in equation (4) obey some common laws of addition and multiplication by real numbers, we may be able to solve all these 4 equations, and many other more complicated questions, using the same algorithm based on the properties (or laws) of addition and multiplication by real numbers.
Classifying sets by their properties helps in solving problems involving different king of mathematical objects such as matrices, polynomials, 2-d vectors, 3-d vectors, n-d vectors, planes in geometry, functions,...and developing ways and methods to solve different problems using the same algorithms.
Definition of a Vector Space
In what follows, vector spaces (1 , 2) are in capital letters and their elements (called vectors) are in bold lower case letters.
A nonempty set V whose vectors (or elements) may be combined using the operations of addition (+) and multiplication · by a scalar is called a vector space if the conditions in A and B below are satified:
Note An element or object of a vector space is called vector.
A) the addition of any two vectors of V and the multiplication of any vectors of V by a scalar produce an element that belongs to V .
Let u and v be any two elelments of the set V and r any real number.
\( \) \( \) \( \) \( \)
1) \( \textbf{u} + \textbf{v} = \textbf{w}\) , \( \textbf{w} \) is an element of the set \( V\) ; we say the set \( V\) is closed under vector addition
2)
\( r \cdot \textbf{u} = \textbf{z} \) , \( \textbf{z} \) is an element of the set \( V\) we say the set \( V\) is closed under scalar multiplication
B) For any vectors \( \textbf{u}, \textbf{v}, \textbf{w} \) in \( V\) and any real numbers \( r \) and \( s \), the two operations described above must obey the following rules :
3) Commutatitivity of vector addition : \( \textbf{u} + \textbf{v} = \textbf{v} + \textbf{u} \)
4) Associativity of vector addition : \( (\textbf{u} + \textbf{v}) +\textbf{w} = \textbf{v} + ( \textbf{u} + \textbf{w}) \)
5) Associativity of multiplication: \( r \cdot (s \cdot \textbf{u}) = (r \cdot s) \cdot \textbf{u} \)
6) A zero vector \( \textbf{0} \) exists in \( \textbf{v}\) and is such that for any element \( \textbf{u}\) in the set \( \textbf{v}\), we have: \( \textbf{u} + \textbf{0} = \textbf{u} \)
7) For each vector \( \textbf{u}\) in \( V\) there exists a vector \( - \textbf{u} \) in \( V\), called the negative of \( \textbf{u}\), such that: \( \textbf{u} + (- \textbf{u}) = \textbf{0} \)
8) Distributivity of Addition of Vectors: \( r \cdot (\textbf{u} + \textbf{v} ) = r \cdot \textbf{u} + r \cdot \textbf{v} \)
9) Distributivity of Addition of Real Numbers: \( (r + s) \cdot \textbf{u} = r \cdot \textbf{u} + s \cdot \textbf{u} \)
10) For any element \( \textbf{u}\) in \( V\) we have: \( 1 \cdot \textbf{u} = \textbf{u} \)
NOTES
1) Although the element of a vector space is called vector, a vector space may be a set of matrices, functions, solutions to differential equations, 3-d vectors, ....,They do not have to be VECTORS of n dimensions such as 2 or 3 dimensional vectors used in physics.
Examples of Vector Spaces
Example 1
The following are examples of vector spaces:
The set of all real number \( \mathbb{R} \) associated with the addition and scalar multiplication of real numbers.
The set of all the complex numbers \( \mathbb{C} \) associated with the addition and scalar multiplication of complex numbers.
The set of all polynomials \( R_n(x) \) with real coefficients associated with the addition and scalar multiplication of polynomials.
The set of all vectors of dimension \( n \) written as \( \mathbb{R}^n \) associated with the addition and scalar multiplication as defined for 3-d and 2-d vectors for example.
The set of all matrices of dimension \( m \times n \) associated with the addition and scalar multiplication as defined for matrices.
The set of all functions \( \textbf{f} \) satisfying the differential equation \( \textbf{f} = \textbf{f '} \)
Example 2
Proove that the set of all 2 by 2 matrices associated with the matrix addition and the scalar multiplication of matrices is a vector space.
Solution to Example 2
Let \( V\) be the set of all 2 by 2 matrices.
1) Addition of matrices gives
\( \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
=
\begin{bmatrix}
a+a' & b+b' \\
c+c' & d+d'
\end{bmatrix}
\)
Adding any 2 by 2 matrices gives a 2 by 2 matrix and therefore the result of the addition belongs to \( V\).
2) Scalar multiplication of matrices gives gives
\( r \begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
=
\begin{bmatrix}
r a & r b \\
r c & r d
\end{bmatrix} \)
Multiply any 2 by 2 matrix by a scalar and the result is a 2 by 2 matrix is an element of \( V\).
3) Commutativity
\( \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
\\\\
=
\begin{bmatrix}
a+a' & b+b' \\
c+c' & d+d'
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a'+a & b'+b \\
c'+c & d'+d
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix} +
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
4) Associativity of vector addition
\(
\left (
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
\right)
+
\begin{bmatrix}
a'' & b'' \\
c'' & d''
\end{bmatrix}
\\ =
\begin{bmatrix}
a+a' & b+b' \\
c+c' & d+d'
\end{bmatrix}
+
\begin{bmatrix}
a'' & b'' \\
c'' & d''
\end{bmatrix}
\\\\ =
\begin{bmatrix}
(a+a')+a'' & (b+b')+b'' \\
(c+c') + c''& (d+d')+d''
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a+(a'+a'') & b+(b'+b'') \\
c+(c' + c'')& d+(d'+d'')
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\left(
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
+
\begin{bmatrix}
a'' & b'' \\
c'' & d''
\end{bmatrix}
\right)
\)
5) Associativity of multiplication
\(
r \left( s \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} \right)
=
r \left( \begin{bmatrix}
s a & s b \\
s c & s d
\end{bmatrix} \right)
\\\\ =
\begin{bmatrix}
r s a & r s b \\
r s c & r s d
\end{bmatrix}
\\\\ =
\begin{bmatrix}
(r s) a & (r s) b \\
(r s) c & (r s) d
\end{bmatrix}
\\\\ =
(r s)
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
6) Zero vector
\( \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
0 & 0 \\
0 & 0
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a+0 & b+0 \\
c+0 & d+0
\end{bmatrix}
=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
7) Negative vector
\( \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
- a & - b \\
- c & - d
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a+(-a) & b+(-b) \\
c+(-c) & d+(-d)
\end{bmatrix}
\\\\ =
\begin{bmatrix}
0 & 0 \\
0 & 0
\end{bmatrix}
\)
8) Distributivity of sums of matrices:
\(
r
\left (
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
\right)
\\\\ =
\begin{bmatrix}
r(a+a') & r(b+b') \\
r(c+c') & r(d+d')
\end{bmatrix}
\\\\ =
\begin{bmatrix}
r a+ r a' & r b+ r b \\
r c+r c' & r d+ r d
\end{bmatrix}
\\\\ =
r \left (
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} \right) + r \left(\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix} \right)
\)
9) Distributivity of sums of real numbers:
\(
(r + s ) \begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
=
\begin{bmatrix}
(r + s ) a & (r + s ) b \\
(r + s ) c & (r + s ) d
\end{bmatrix}
\\\\=
\begin{bmatrix}
r a + s a & r b + s b \\
r c + s c & r d + s d
\end{bmatrix}
\\\\=
\begin{bmatrix}
r a & r b \\
r c & r d
\end{bmatrix} + \begin{bmatrix}
s a & s b \\
s c & s d
\end{bmatrix}
\\\\=
r \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} + s \begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
10) Multiplication by 1.
\( 1 \begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
=
\begin{bmatrix}
1 a & 1 b \\
1 c & 1 d
\end{bmatrix}
=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
Example 3
Show that the set of all real functions continuous on \( (-\infty,\infty) \) associated with the addition of functions and the multiplication of matrices by a scalar form a vector space.
Solution to Example 3
From calculus, we know if \( \textbf{f} \) and \( \textbf{g} \) are real continuous functions on \( (-\infty,\infty) \) and \( r \) is a real number then
\( (\textbf{f} + \textbf{g})(x) = \textbf{f}(x) + \textbf{g}(x) \) is also continuous on \( (-\infty,\infty) \)
and
\( r \textbf{f}(x) \) is also continuous on \( ( -\infty,\infty ) \)
Hence the set of functions continuous on \( (-\infty,\infty) \) is closed under addition and scalar multiplication (the first two conditions above).
The remaining 8 rules are automatically satisfied since the functions are real functions.
Example 4
Show that the set of all real polynomials with a degree \( n \le 3 \) associated with the addition of polynomials and the multiplication of polynomials by a scalar form a vector space.
Solution to Example 4
The addition of two polynomials of degree less than or equal to 3 is a polynomial of degree lass than or equal to 3.
The multiplication, of a polynomial of degree less than or equal to 3, by a real number results in a polynomial of degree less than or equal to 3
Hence the set of polynomials of degree less than or equal to 3 is closed under addition and scalar multiplication (the first two conditions above).
The remaining 8 rules are automatically satisfied since the polynomials are real.
Example 5
Show that the set of polynomials with a degree \( n = 4 \) associated with the addition of polynomials and the multiplication of polynomials by a real number IS NOT a vector space.
Solution to Example 5
The addition of two polynomials of degree 4 may not result in a polynomial of degree 4.
Example: Let \( \textbf{P}(x) = -2 x^4+3x^2- 2x + 6 \) and \( \textbf{Q}(x) = 2 x^4 - 5x^2 + 10 \)
\( \textbf{P}(x) + \textbf{Q}(x) = (-2 x^4+3x^2- 2x + 6 ) + ( 2 x^4 - 5x^2 + 10) = - 5x^2 - 2 x + 16 \)
The result is not a polynomial of degree 4. Hence the set is not closed under addition and therefore is NOT vector space.
Example 6
Show that the set of integers associated with addition and multiplication by a real number IS NOT a vector space
Solution to Example 6
The multiplication of an integer by a real number may not be an integer.
Example: Let \( x = - 2 \)
If you multiply \( x \) by the real number \( \sqrt 3 \) the result is NOT an integer.
More References and links
Linear Algebra and its Applications - 5 th Edition - David C. Lay , Steven R. Lay , Judi J. McDonald
Elementary Linear Algebra - 7 th Edition - Howard Anton and Chris Rorres
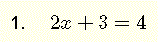this equation involves sums of real expressions and multiplications by real numbers
this equation involves sums of 2-d vectors and multiplications by real numbers
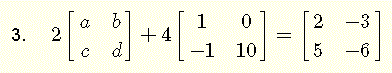this equation involves sums of 2 by 2 matrices and multiplications by real numbers
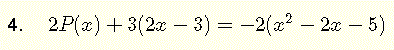this equation involves sums of polynommials and multiplications by real numbers.
