Find a Logarithmic Function Given Its Graph

In this tutorial, we will learn how to find a possible equation of a logarithmic function from its graph. Step-by-step examples are provided to demonstrate how to identify vertical asymptotes, set up algebraic equations, and solve for the unknown parameters.

Table of Contents

Logarithmic Functions: General Form & Properties

A general logarithmic function can be written in the form:

\[ f(x) = a \log_b (x - c) + d \]

Before working through the examples below, it is recommended to review the tutorial on graphing logarithmic functions.

Meaning of Each Parameter

Parameter Effect on the Graph
\( a \)Vertical stretch or compression. If \( a \lt 0 \), the graph is also reflected across the \( x \)-axis.
\( b \)Base of the logarithm. Determines the steepness of the curve. Must satisfy \( b \gt 0 \) and \( b \ne 1 \).
\( c \)Horizontal shift. Determines the location of the vertical asymptote \( x = c \).
\( d \)Vertical shift. Moves the entire graph up or down.

Important Properties of \( f(x) = a \log_b (x - c) + d \):

When solving these problems, it is crucial to recall the fundamental relationship between logarithmic and exponential functions:

\[ y = \log_b (x) \quad \Longleftrightarrow \quad b^y = x \]

This equivalence is the key tool for converting logarithmic equations into exponential form when solving for the base or the shift parameter.

How to Find the Equation: Step-by-Step

  1. Identify the vertical asymptote: Read the value \( x = c \) from the graph. This immediately gives the horizontal shift \( c \).
  2. Identify clear points: Choose two or more points with easy-to-read integer coordinates that lie exactly on the curve.
  3. Substitute into the general form: Plug each point into \( f(x) = a \log_b(x - c) + d \) to set up a system of equations.
  4. Solve the system: Use substitution or elimination to find \( a \), \( b \), and \( d \).
  5. Verify: Confirm that all points satisfy the resulting equation.

Examples with Detailed Solutions

Example 1: Finding the Base

Show Solution

Question: Find the logarithmic function of the form \( y = \log_b(x) \) whose graph is shown below.

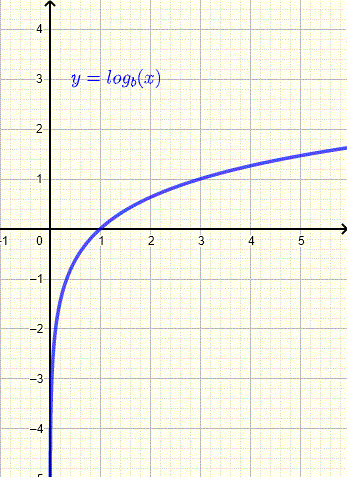
Graph of logarithmic function for Example 1 passing through the point (3,1)

Solution

Observe the graph to find a clear coordinate point. The point \( (3,1) \) lies exactly on the graph.

Substitute \( x = 3 \) and \( y = 1 \) into the equation \( y = \log_b(x) \):

\[ 1 = \log_b(3) \]

Rewrite this logarithmic equation in its equivalent exponential form:

\[ b^1 = 3 \quad \Rightarrow \quad b = 3 \]

Answer: The logarithmic function is \( y = \log_3(x) \).

Verification: \( \log_3(3) = 1 \) ✓ and the vertical asymptote is at \( x = 0 \) ✓

Example 2: Finding a Horizontal Shift

Show Solution

Question: Find the logarithmic function of the form \( y = \log_b(x - c) \).

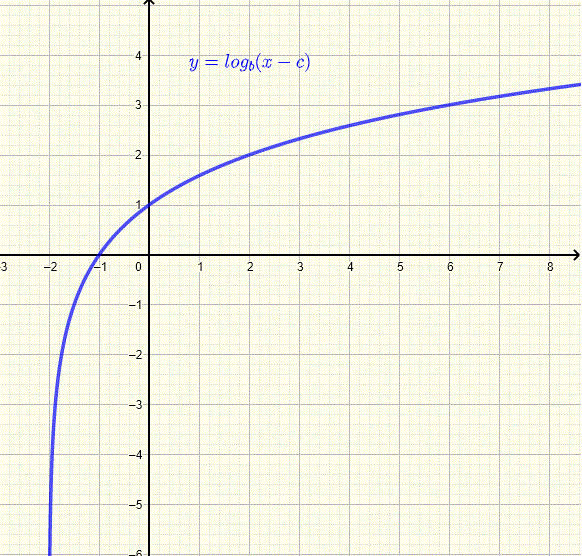
Graph of logarithmic function for Example 2 passing through points (-1,0) and (2,2)

Solution

Identify two points from the graph. The points \( (-1,0) \) and \( (2,2) \) lie on the curve.

Substitute both points into the general equation \( y = \log_b(x - c) \) to create a system of equations:

  • From \( (-1,0) \): \( 0 = \log_b(-1 - c) \)
  • From \( (2,2) \): \( 2 = \log_b(2 - c) \)

Convert the first equation to exponential form to solve for \( c \):

\[ b^0 = -1 - c \]

Since \( b^0 = 1 \), we have:

\[ 1 = -1 - c \quad \Rightarrow \quad c = -2 \]

Now, substitute \( c = -2 \) into the second equation:

\[ 2 = \log_b(2 - (-2)) \]

\[ 2 = \log_b(4) \]

Convert this to exponential form to find \( b \):

\[ b^2 = 4 \quad \Rightarrow \quad b = 2 \]

(Note: We take the positive root because the base of a logarithm must be positive.)

Answer: The function is \( y = \log_2(x + 2) \).

Verification: \( \log_2(-1+2) = \log_2(1) = 0 \) ✓ and \( \log_2(2+2) = \log_2(4) = 2 \) ✓

Example 3: Solving for Multiplier and Shift

Show Solution

Question: Find the logarithmic function of the form \( y = a \log_4(x - c) \).

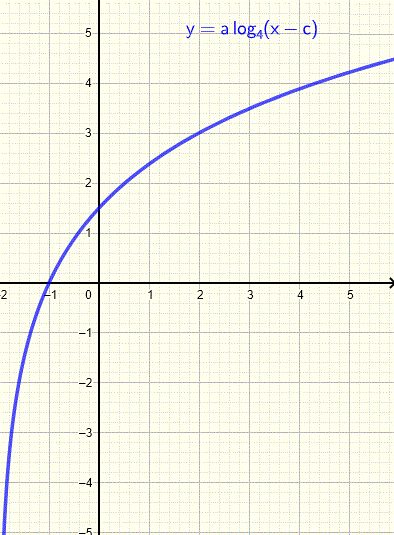
Graph of logarithmic function for Example 3 passing through (-1,0) and (2,3)

Solution

From the graph, identify the points \( (-1,0) \) and \( (2,3) \).

Substitute these points into the equation:

  • \( 0 = a \log_4(-1 - c) \)
  • \( 3 = a \log_4(2 - c) \)

Divide the first equation by \( a \) (assuming \( a \neq 0 \)):

\[ \log_4(-1 - c) = 0 \]

Convert to exponential form to solve for \( c \):

\[ 4^0 = -1 - c \]

\[ 1 = -1 - c \quad \Rightarrow \quad c = -2 \]

Substitute \( c = -2 \) into the second equation:

\[ 3 = a \log_4(2 - (-2)) \]

\[ 3 = a \log_4(4) \]

Since \( \log_4(4) = 1 \):

\[ 3 = a(1) \quad \Rightarrow \quad a = 3 \]

Answer: The function is \( y = 3 \log_4(x + 2) \).

Verification: \( 3\log_4(-1+2) = 3\log_4(1) = 0 \) ✓ and \( 3\log_4(2+2) = 3\log_4(4) = 3 \) ✓

Example 4: Finding Asymptotes and Shifts

Show Solution

Question: Find the logarithmic function of the form \( y = a \log_2(x - c) + d \) with a vertical asymptote at \( x = 1 \).

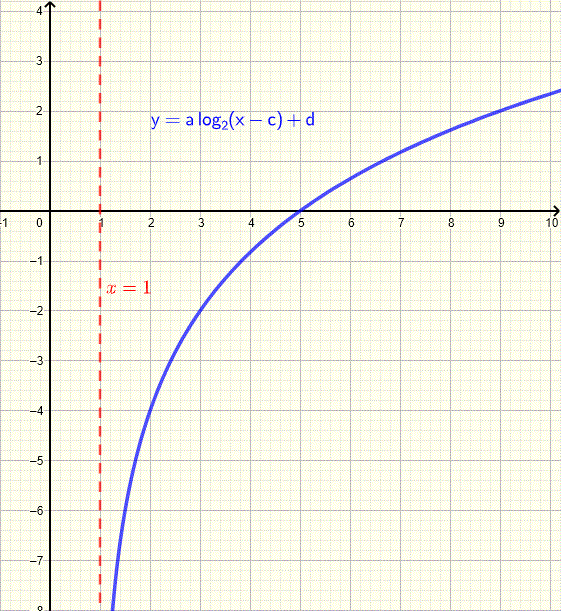
Graph of logarithmic function for Example 4 with asymptote at x = 1

Solution

The vertical asymptote occurs where the argument is zero (\( x - c = 0 \)). Given the asymptote is \( x = 1 \), we know immediately that:

\[ c = 1 \]

Identify two points from the graph, such as \( (5,0) \) and \( (9,2) \), and substitute them into \( y = a \log_2(x - 1) + d \):

  • \( 0 = a \log_2(5 - 1) + d \quad \Rightarrow \quad 0 = a \log_2(4) + d \)
  • \( 2 = a \log_2(9 - 1) + d \quad \Rightarrow \quad 2 = a \log_2(8) + d \)

Evaluate the logarithms (\( \log_2(4) = 2 \) and \( \log_2(8) = 3 \)):

\[ 0 = 2a + d \]

\[ 2 = 3a + d \]

Subtract the first equation from the second to eliminate \( d \):

\[ 2 - 0 = (3a + d) - (2a + d) \]

\[ 2 = a \]

Substitute \( a = 2 \) back into \( 0 = 2a + d \):

\[ 0 = 2(2) + d \quad \Rightarrow \quad d = -4 \]

Answer: The final equation is \( y = 2 \log_2(x - 1) - 4 \).

Verification: \( 2\log_2(5-1) - 4 = 2(2) - 4 = 0 \) ✓ and \( 2\log_2(9-1) - 4 = 2(3) - 4 = 2 \) ✓

Example 5: Full Parameter Search

Show Solution

Question: Find the logarithmic function of the form \( y = a \log_2(x - c) + d \) with a vertical asymptote at \( x = 0 \).

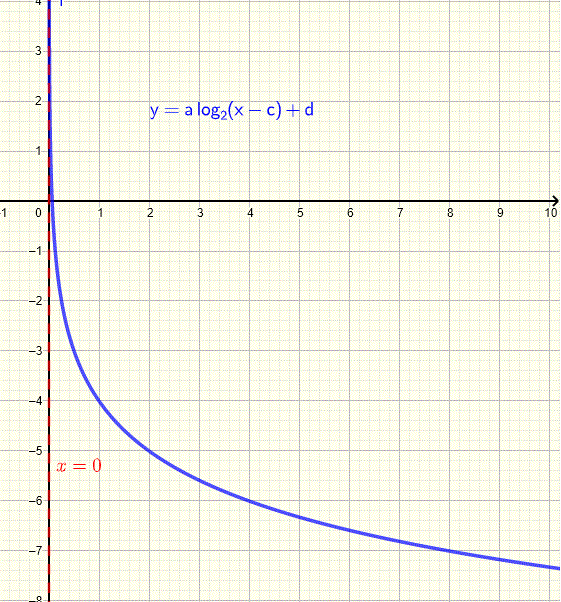
Graph of logarithmic function for Example 5 with asymptote at x = 0

Solution

The vertical asymptote is at \( x = 0 \), meaning the argument becomes zero at \( x = 0 \). Therefore:

\[ c = 0 \]

Using points from the graph (such as \( (2,-5) \) and \( (4,-6) \)), set up a system of equations by substituting into \( y = a \log_2(x) + d \):

\[ -5 = a \log_2(2) + d \quad \Rightarrow \quad a + d = -5 \]

\[ -6 = a \log_2(4) + d \quad \Rightarrow \quad 2a + d = -6 \]

Subtract the first equation from the second equation to isolate \( a \):

\[ (-6) - (-5) = (2a + d) - (a + d) \]

\[ -1 = a \]

Substitute \( a = -1 \) into \( a + d = -5 \):

\[ -1 + d = -5 \quad \Rightarrow \quad d = -4 \]

Answer: The final equation is \( y = -\log_2(x) - 4 \).

Verification: \( -\log_2(2) - 4 = -1 - 4 = -5 \) ✓ and \( -\log_2(4) - 4 = -2 - 4 = -6 \) ✓

Common Mistakes to Avoid

  1. Confusing the horizontal shift with the asymptote. The asymptote is at \( x = c \), not \( x = -c \). For example, in \( \log(x - 3) \), the asymptote is at \( x = 3 \).
  2. Using a point that is not exactly on the curve. Always choose points with clear integer coordinates that visibly lie on the graph.
  3. Forgetting to take the positive root for the base. When solving \( b^2 = 4 \), we use \( b = 2 \), not \( b = -2 \), because the base must be positive.
  4. Mixing up \( a \) and \( d \). The parameter \( a \) stretches the graph vertically, while \( d \) shifts it up or down.
  5. Assuming the base is 10 by default. The base \( b \) must be determined from the graph; only \( \log \) without a subscript means base 10.

Exercises with Answers

Practice by finding the equations for the logarithmic graphs presented below:

Three exercises showing graphs of logarithmic functions to identify
View Answers
  1. A) \( \quad y = \log_{1/2}(x) \)
  2. B) \( \quad y = -2 \log_3(x - 2) \)
  3. C) \( \quad y = 3 \log_2(x + 2) - 2 \)

Hint: Identify the vertical asymptote first to find \( c \), then use two points to solve for the remaining parameters.

Frequently Asked Questions

How do you find the equation of a logarithmic function from its graph?

To find the logarithmic function from a graph: (1) Identify the vertical asymptote \( x = c \), since the argument \( x - c \) must equal zero there. (2) Identify two or more clear points on the curve. (3) Substitute the points into the general form \( y = a \log_b(x - c) + d \). (4) Solve the resulting system of equations for the unknown parameters.

What is the general form of a logarithmic function?

The general form of a logarithmic function is \( f(x) = a \log_b(x - c) + d \), where \( a \) is the vertical stretch/compression factor, \( b \) is the base (\( b \gt 0 \) and \( b \ne 1 \)), \( c \) determines the vertical asymptote at \( x = c \), and \( d \) is the vertical shift.

How do you find the vertical asymptote of a logarithmic function?

The vertical asymptote occurs where the argument of the logarithm equals zero. For \( f(x) = a \log_b(x - c) + d \), set \( x - c = 0 \), giving the vertical asymptote \( x = c \).

Why must the base of a logarithm be positive and not equal to 1?

The base \( b \) must satisfy \( b \gt 0 \) and \( b \ne 1 \). If \( b \) were negative, exponential expressions \( b^x \) would be undefined for non-integer \( x \). If \( b = 1 \), then \( b^x = 1 \) for all \( x \), so \( \log_1 \) would not be a well-defined function.

What is the domain and range of a logarithmic function?

For \( f(x) = a \log_b(x - c) + d \), the domain is \( (c, +\infty) \) because the argument \( x - c \) must be strictly positive. The range is all real numbers, \( (-\infty, +\infty) \), because logarithmic functions produce every real value.

Can a logarithmic function of the form \( f(x) = a \log_b(x - c) + d \) have no vertical asymptote?

No. Every basic logarithmic function of the form \( f(x) = a \log_b(x - c) + d \) has exactly one vertical asymptote, located at \( x = c \). The asymptote is inherent to the logarithmic structure because the argument approaches zero from the right.

Further Reading