Solutions to Grade 7 Math Practice Test

The solutions to the Grade 7 math practice test questions are presented.

1 - Integers

Solutions

The absolute value of a number is either positive or zero and therefore only part b) is true.
All the numbers involved in the given inequalities are plotted on the number line below and given any two numbers on the number line, the one on the right is larger than the one on the left or the number on the left is smaller than the one on the right.

Hence:
a) is NOT TRUE (-5 to the right of - 7) b) is TRUE ,
c) is NOT TRUE (-1 to the left of 0) d) is TRUE
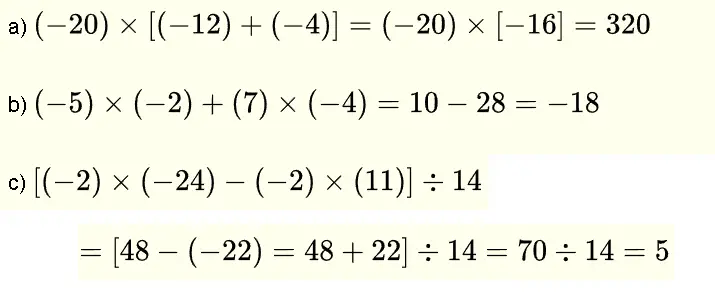
2 - Decimals

Solutions
Write the numbers in a table including the place value as as shown below
 $ \require{cancel} $
1) We compare the digits in the ones and they are all equal
2) We next compare the tenths and the highest is the the one corresponding to the number in the first row. $ 2.32 $ is the largest.
3) We next compare the hundredths and the two highest are in the second and fourth rows.
4) We next compare the thousandths of the numbers in the the second and fourth rows and the one in the fourth is the highest. $ 2.033 $ is the second largest.
5) $ 2.032 $ is the third largest and $ 2.032 $ is the fourth largest.
The order from largest to smallest is: $ 2.32 $ , $ 2.033 $ , $ 2.032 $ , $ 2.023 $
a) $ 4.01 $ has a $ 0 $ in the tenth, hence no change to the ones digit and therefore the answer is $ 4 $
b) $ 6.8 $ has an $ 8 $ in the tenth, hence we add $ 1 $ to the ones digit and therefore the answer is $ 7 $
c) $ 11.5 $ has a $ 5 $ in the tenth, hence we add $ 1 $ to the ones digit and therefore the answer is $ 12 $
a) $ 0.15 \div 3 = 0.05$
b) $ 5 - 1.2 \times 0.2 = 5 - 0.24 = 4.76 $
c) $ 2.3 - 0.7 \div 7 = 2.3 - 0.1 = 2.2$

3 - Factors, Multiples and Divisibility of Numbers

Solutions
The factors of $ 18 $ are: $ 1, 2, 3, \color{red}6, 9, 18 $
The factors of $ 24 $ are: $ 1, 2, 3, 4, \color{red}6, 8, 12, 24 $
The Greatest Common Factor (GCF) of $ 24 $ and $ 18 $ is $ \color{red}6 $
The multiples of $ 8$ are: $ 8, 16, 24, 32, 40, 48, 56, 64,\color{red}{72}, 80 $
The multiples of $ 18 $ are: $ 18, 36, 54, \color{red}{72}, 90 $
the Least Common Multiple (LCM) of $ 8 $ and $ 18 $ is $ \color{red}{72} $
A number whose last digit in the ones (furthest to the right) is $ 0 $ or $ 5 $ is divisible by $ 5 $.
Hence the numbers in part b) $ 303090 $ and c) $ 145055 $ are divisible by $ 5 $.
A number whose last digit in the ones (furthest to the right) is $ 0, 2, 4, 6 , 8 $ is divisible by $ 2 $.
Hence the numbers in part a) $ 2798 $ and c) $ 6476 $ are divisible by $ 2 $.
A number is divisible by $ 3 $ if the sum of all its digits in the number is divisible by $ 3 $ (or is a multiple of $ 3 $)
a) $ 9240 $ : sums of digits: $ 9+2+4+0 = 15 $ , $ 15 $ is divisible by $ 3 $ and therefore $ 9240 $ is divisible by 3.
b) $ 4 909 $: sums of digits: $ 4+9+0+9 = 22 $ , $ 22 $ is divisible by $ 3 $ and therefore $ 4 909 $ is NOT divisible by 3.
c) $ 3 282 900 $ : sums of digits: $ 3+2+8+2+9+0+0 = 24 $ , $ 24 $ is divisible by $ 3 $ and therefore $ 3 282 900 $ is divisible by 3.

4 - Fractions and Mixed Numbers

Solutions
We can obtain an equivalent fraction to a given one by multiplying or dividing the numerator and denominator of the given fraction by the same number.
a)
Given $ \displaystyle \frac{10}{15} = \frac{?}{3}$
To go from a denominator equal to $ 15 $ in the fraction on the left to a denominator equal to $ 3 $ in the fraction on the right, we divide by $ 5 $. Hence
$ \displaystyle \frac{10}{15} = \frac{10 \color{red}{\div 5}}{15 \color{red}{\div 5}} = \frac{2}{3} $

b)
Given $ \displaystyle \frac{17}{3} = \frac{34}{?} $
To go from a numerator equal to $ 17 $ in the fraction on the left to a numerator equal to $ 34 $ in the fraction on the right, we multiply by $ 2 $. Hence
$ \displaystyle \frac{17}{3} = \frac{17 \color{red}{\times 2} }{3 \color{red}{\times 2} } = \frac{34}{6} $

c)
Given $ \displaystyle \frac{11}{2} = \frac{?}{8} $
To go from a denominator equal to $ 2 $ in the fraction on the left to a denominator equal to $ 8 $ in the fraction on the right, we multiply by $ 4 $. Hence
$ \displaystyle \frac{11}{2} = \frac{11 \color{red}{\times 4}}{2 \color{red}{\times 4}} = \frac{44}{8} $
a)
Convert the fraction $ \displaystyle \frac{2}{5} $ to an equivalent fraction with denominator equal to $ 10 $
$ \displaystyle \frac{2}{5} = \frac{2 \times 2}{5 \times 2} = \frac{4}{10} $
Substitute the fraction $ \displaystyle \frac{2}{5} $ by its equivalent in the given expression
$ \displaystyle \frac{2}{5} + \frac{3}{10} - \frac{1}{10} = \frac{4}{10} + \frac{3}{10} - \frac{1}{10} $
The fractions in the sum/difference have the same denominator and we therefore add/subtract tham as follows
$ \displaystyle \frac{2}{5} + \frac{3}{10} - \frac{1}{10} \\ = \displaystyle \frac{4}{10} + \frac{3}{10} - \frac{1}{10} = \frac{4+3-1}{10} = \frac{6}{10} $
Reduce the fraction by dividing numerator and denominator by $ 2 $ and hence
$ \displaystyle \frac{2}{5} + \frac{3}{10} - \frac{1}{10} = \frac{3}{5} $

b)
$ \displaystyle \frac{5}{9} \times \frac{3}{4} = \frac {5 \times 3}{9 \times 4} = \frac{15}{36}$
Divide numerator and denominator by the GCF of $ 15 $ and $ 36 $ which is $ 3 $
$ \displaystyle = \frac{15 \div 3}{36 \div 3} = \frac{5}{12}$

c)
To divide a fraction by another we multiply the first by the inverse of the second. Hence
$ \displaystyle \frac{11}{2} \div \frac{1}{8} = \frac{11}{2} \times \frac{8}{1} = \frac{88}{2} = 44$

d)
$ \displaystyle 4 \frac{3}{4} - 1 \frac{1}{2} = (4 - 1) + (\frac{3}{4} - \frac{1}{2}) $
Convert $ \displaystyle \frac{1}{2} $ to an equivalent fraction with denominator equal to $ 4 $ and substitute
$ \displaystyle = 3 + (\frac{3}{4} - \frac{2}{4}) = 3 \frac{1}{4} $

e)
Convert the mixed number $ \displaystyle 6 \frac{3}{4} $ to a fraction
$ \displaystyle 6 \frac{3}{4} = 6 + \frac{3}{4} = \frac{24}{4} + \frac{3}{4} = \frac{27}{4} $
The division is done by mutliplying by the inverse of $ 2 $. Hence
$ \displaystyle \frac{27}{4} \times \frac{1}{2} = \frac{27}{8}$
Convert to a mixed number
$ \displaystyle \frac{27}{8} = \frac{24+3}{8} = 3 \frac{3}{8}$

f)
Write $ 3 $ as fraction.
$ \displaystyle 3 = \frac{3}{1} $
The division becomes a multiplication by the inverse of $ \displaystyle \frac{3}{5} $. Hence
$ \displaystyle 3 \div \frac{3}{5} = \frac{3}{1} \times \frac{5}{3} = 5 $

g)
Convert the mixed numbers into improper fractions
$ \displaystyle 2 \frac{3}{5} = 2 + \frac{3}{5} = \frac{2}{1} + \frac{3}{5} = \frac{2 \times 5}{1 \times 5} + \frac{3}{5} = \frac{13}{5} $
$ \displaystyle 3 \frac{3}{5} = 3 + \frac{3}{5} = \frac{3 \times 5}{1 \times 5} + \frac{3}{5} = \frac{18}{5} $
Substitute the mixed numbers by the equivalent fractions found above
$ \displaystyle 2 \frac{3}{5} \div 3 \frac{3}{5} = \frac{13}{5} \div \frac{18}{5} $
A division of fractions becomes a multiplication by the inverse.
$ \displaystyle 2 \frac{3}{5} \div 3 \frac{3}{5} = \frac{13}{5} \times \frac{5}{18} = \frac{13}{18} $
a)
The number has the digit $ 2 $ in the tenth. Hence
$ 0.2 = \displaystyle \frac {2}{10} $
Reduce the fractions
$ = \displaystyle \frac {1}{5} $

b)
The number has $1 $ in the units, $ 2 $ in the tenths and $ 4 $ in the hundredths. Hence
$ \displaystyle 1.24 = 1 + \frac{2}{10} + \frac{4}{100} = 1 + \frac{2 \times 10}{10 \times 10} + \frac{4}{100} = 1 \frac{24}{100} $
Reduce the fraction
$ \displaystyle = 1 \frac{6}{25} $

c)
$ \displaystyle 2.326 = 2 + \frac{3}{10} + \frac{2}{100} + \frac{6}{1000} = 2 \frac{163}{500} $
Use rules of division by $ 10 $, $ 100$, $ 1000 $, $ 10000 $, ...
a)
$ \displaystyle \frac{9}{100} = 0.09 $
b)
$ \displaystyle \frac{17}{10000} = 0.0017$
c)
$ \displaystyle 3 \frac{11}{100000} = 0.00011$
a)
Convert the fractions to the same denominator
$ \displaystyle \frac{2}{5} = \frac{8}{20} $
$ \displaystyle \frac{3}{4} = \frac {15}{20} $
Hence the statement $ \displaystyle \frac{2}{5} \lt \frac{3}{4} $ is true

b)
Convert the fractions to the same denominator
$ \displaystyle \frac{1}{3} = \frac{10}{30} $
$ \displaystyle \frac{3}{10} = \frac {9}{30} $
Hence the statement $ \displaystyle \frac{1}{3} \lt \frac{3}{10} $ is NOT true

5 - Exponents

Solutions
a)
$ 3 \times 3 \times 3 \times 3 = 3^4 $
b)
$ 7 \times 4 \times 4 \times 4 \times 5 \times 5 = 7 \times (4 \times 4 \times 4 \times) \times (5 \times 5) = 7 \times 4^3 \times 5^2$
a)
$ 2^4 = 2 \times 2 \times 2 \times 2 = 16 $
b)
$ 3^2 \times 4^2 = (3 \times 3) \times (4 \times 4) = 9 \times 16 = 144$
c)
Note that $ 10^0 = 1 $, hence
$ 10^0 \times 4^2 = 1 \times 4 \times 4 = 16 $

6 - Ratios and Rates and Related

Solutions
a) triangles to squares : 4 to 7 b) squares to triangles : 7 to 4 c) squares to total numbers of figures: 7:11
School A: $ 1200 $ students , $ 400 $ boys , girls $ 1200 - 400 = 800$, ratio girls to boys as a fraction: $ \displaystyle \frac{800}{400} $ which reduces to $ \displaystyle \frac{2}{1} $

School B: $ 800 $ students , $ 300 $ boys , girls $ 800 - 300 = 500$, ratio girls to boys as a fraction: $ \displaystyle \frac{500}{300} $ which reduces to $ \displaystyle \frac{5}{3} $
Compare the ratios given by the fractions and converted to a common denominator
School A: $ \displaystyle \frac{2}{1} = \frac{6}{3} $
School B: $ \displaystyle \frac{5}{3} $
Comparing the ratios given by the fractions, school A has a higher girls to boys ratio.
Unit rate: $ \displaystyle \frac{\$15}{5 \; \text{kg}} = 3 \; \$/\text{kg} $
Unit rate: $ \displaystyle \frac{350 \; \text{km}}{5 \; \text{hrs}} = 70 \; \text{km} / \text{hrs}$

7 - Proportionality and Related Problems

Solutions
Distance id proportional to time as follows:
Distance = speed � time , the speed (or rate) is constant
speed = $ \displaystyle \frac{240 \; \text{km}}{3 \; \text{hrs}} = 80 \; km/hrs $
$ 400 \; km $ = speed � time
time = $ \displaystyle \frac{400 km}{80 \; km/hrs } = 5 \; \text{hrs}$
Let $ x $ the amount in dollars needed to buy 320 Dirhams.
rate of change: $ 4 \; \text{Dhs/\$} $ and is constant
$ 320 \; \text{Dhs} = x \times \; 4 \; \text{Dhs/\$}$
$ x = \displaystyle \frac{320 \; \text{Dhs} }{4 \; \text{Dhs/\$}} = 80 \; \text{\$} $
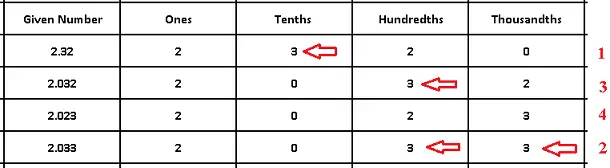
a)
Distance = $ k \times$ time
From the graph at time = $ 2 $ hrs the distance d = $ 8 $ km
Hence
$ 8 = k \times 2 $
Calculate $ k $
$ k = 8/2 = 4 $
for time = 2.5 hrs;
d = $ 4 � 2.5 = 10 $ km
b)
It is the constant $ k = 4 $ km/hrs
c)
Using Distance = $ k \times $ time, we write
$ 32 = 4 \times $ time
time needed to cover $ 32 $ km is given by $ 32 / 4 = 8 $ hrs,
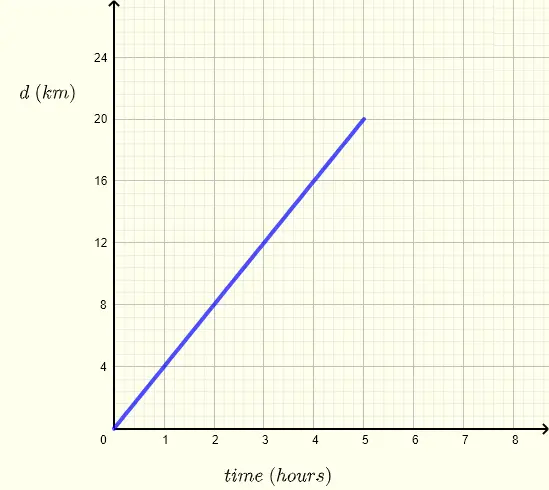
For $ y $ to be proportional to $ x $, we need to have the relationship \[ y = k x \] where $ k $ must be constant
The above relationship may also be written as \[ \frac{y}{x} = k \] Below is shown the same tables completed by the ratio $ y \div x $ on the right
The ratios $ y \div x $ in the tables A) and C) are NOT constant (see red circle).
However the ratios $ y \div x $ in the tables B) and D) are constant and equal to $ 2 $ and $ 3 $ respectively.
Hence $ y $ is proportional to $ x $ in tables B) and D) but not A) and C)

8 - Percent and Related Problems

Solutions
$ \displaystyle 20\% $ of $ \displaystyle 10 = \frac{20}{100} \times 10 = \frac{200}{100} = 2 $
$ 50\% $ of $ \displaystyle \frac{1}{4} = \frac{50}{100} \times \frac{1}{4} = \frac{50}{400} = \frac{1}{8} $
A percent is a fraction with denominator equal to 100. Hence to go from denominator equal to $ 5 $ to a denominator equal to $ 100 $, we multiply by $ 20 $.
$ \displaystyle \frac {3}{5} = \frac {3 \times 20}{5 \times 20} = \frac{60}{100} = 60\% $
Percent of her monthly salary spent on clothes = $ \displaystyle \frac {600}{3000} = \frac {600 \div 30}{3000 \div 30 } = \frac{20}{100} = 20\% $
Change in percent = $ \displaystyle \frac{100 - 120}{100} = \frac{-20}{100} = - 20 \% $
Let $ x $ be the number such that $ 10\% $ of $ x = 3 $
$ 10\% $ of $ x = \displaystyle \frac {10}{100}\times x = \frac{10 x}{100} $
Hence the equation
$ \displaystyle \frac{10 x}{100} = 3 $
Multiply both sides of the equation by $ 100 $
$ \displaystyle \frac{10 x}{100} \times 100= 3 \times 100 $
Simplify
$ 10 x = 300 $
Solve for $x $
$ x = 30 $
After 20% increase the price becomes
$ 40 + 20\% \times 40 = \$48 $
After 20% decrease (of last price) final price of shirt is
$ 48 - 20\% \times 48 = 48 - 9.6 = \$38.4$

9 - Convert Units of Measurement

Solutions
Divide both sides of the given equality $ 1 \text{ km} = 1000 \text{ m} $ by $ 1 \text{ km} $ to obtain a factor of conversion given by \[ \frac {1000 \text{ m}}{1 \text{ km}} = 1\] We now write that $ 1.2 \text{ km} = 1.2 \text{ km} \times 1 $ The factor of conversion found above is also equal to 1 , hence the substitution \[ \displaystyle 1.2 \text{ km} = 1.2 \text{ km} \times \frac {1000 \text{ m}}{1 \text{ km}} \] Cancel $ \text{ km} $ \[ \displaystyle 1.2 \text{ km} = 1.2 \cancel{\text{ km}} \times \frac {1000 \text{ m}}{1 \cancel{\text{ km}}} \] Simplify and evaluate \[ 1.2 \text{ km} = 1200 \text{ m} \]
Divide both sides of the given equality $ 1 \text{ US gal} = 3.78541 \text{ L} $ by $ 3.78541 \text{ L} $ to write the factor of conversion \[ \displaystyle \frac{1 \text{ US gal}}{3.78541 \text{ L}} = 1 \] We now write \[ 120 \text{ L} = 120 \text{ L} \times 1 \] and substitute $ 1 $ by the factor of conversion which also equal to $ 1 $ \[ \displaystyle 120 \text{ L} = 120 \text{ L} \times \frac{1 \text{ US gal}}{3.78541 \text{ L}} \] Cancel $ \text{ L} $ \[ \displaystyle 120 \text{ L} = 120 \cancel{\text{ L}} \times \frac{1 \text{ US gal}}{3.78541 \cancel{\text{ L}}} \] Simplify and evaluate \[ \displaystyle 120 \text{ L} = \frac{120 \times 1 \text{ US gal}}{3.78541 } = 31.70066 \text{ US gal} \]
Note that the symbol $ m^2 $ read as "square meter" may be written as $ m^2 = m \times m$ and the symbol $ ft^2 $ read as "square feet" may be written as $ ft^2 = ft \times ft$.
Multiply each side of the given equality $ 1 \text{ m} = 3.28084 \text{ ft} $ by itself (square) to obtain \[ (1 \text{ m})(1 \text{ m}) = (3.28084 \text{ ft})(3.28084 \text{ ft}) \] Simplify to obtain an equality with $ m^2 $ and $ ft^2 $ \[ 1 \; m^2 = 10.76391 \; ft^2 \] Divide both sides by $ 1 \; m^2 $ to obtain a factor of conversion given by \[ \displaystyle \frac{ 10.76391 \; ft^2 }{1 \; m^2} = 1 \] Write $ 0.3 \; m^2 $ as \[ 0.3 \; m^2 = 0.3 \; m^2 \times 1 \] Substitute the $ 1 $ by the factor of conversion which also equal to $ 1 $ \[ 0.3 \; m^2 = 0.3 \; m^2 \times \displaystyle \frac{ 10.76391 \; ft^2 }{1 \; m^2} \] Cancel $ m^2 $ \[ 0.3 \; m^2 = 0.3 \; \cancel{m^2} \times \displaystyle \frac{ 10.76391 \; ft^2 }{1 \; \cancel{m^2}} \] Simplify and evaluate \[ 0.3 \; m^2 = \displaystyle \frac{ 0.3 \times 10.76391 \; ft^2 }{1} = 3.229173 \; ft^2 \]
Given the rate $ 60 $ kilometers per hour may be written as \[ \displaystyle \frac{60 \; km}{hr} \] Convert $ km $ to $ m $ and $ hr $ to minutes ( $min$ ) using the fact that $1 km = 1000 \; m $ and $ 1 \; hr = 60 \; min $ \[ \displaystyle \frac{60 \; km}{hr} = \frac{60 \times 1000 \; m }{60 \; min} \] Simplify \[ \displaystyle \frac{60 \; km}{hr} = \frac{60 \times 1000 \; m}{60 \; min} = 1000 \; m/min\]

10 - Evaluate Expressions

Solutions
Given expression $ \; 2x - 2 \; $
Substitute $ x $ by $ -2 $ in the given expression
\[ 2 \times(-2) - 2 \] Evaluate \[ = -4 -2 = -6\]
Given expression $ \; | -5 + b | \; $
Substitute $ b $ by $ -10 $ in the given expression
\[ \; | -5 + (-10) | \; \]
Evaluate
\[ = | -5 -10 | = | -15 | = 15 \]
Given expression $ \; a - b \; $
Substitute $ a $ by $ -5 $ and $ b $ by $ -8 $ in the given expression
\[ \; -5 - (-8) = - 5 + 8 = 3 \; \]

11 - Algebra

Solutions
a)
Group like terms
\[ 3x - 2 + 4 x - 5 = (3x+4x) + (-2-5)\]
Simplify
\[ = 7x + (-7) = 7 x - 7\]
b)
Expand the brackets
\[ 3 (a + b + 2 ) + a + 4b - 12 = 3 a + 3 b + 6 + a + 4b - 12 \]
Group like terms
\[ = (3a + a) + (3b+4b) + (6-12) \]
Simplify
\[ = 4 a + 7 b - 6\]
c)
\[ \displaystyle \frac{1}{3}( 6 x + 9) + 3 \]
Expand the brackets
\[ = \displaystyle \frac{1}{3}( 6 x) + \frac{1}{3} (9) + 3 \]
Simplify
\[ 2x + 3 + 3 = 2x + 6\]
d)
Use factoring to write the given expression as follows
\[ 0.2 x + x = (0.2+1) x \]
Simplify
\[ = 1.2 x \]
Factor the expressions
a)
$ 14 x - 2 = \color{red}2 \times 7 x - \color{red}2 \times 1 = \color{red}2 (7x-1)$
b)
$ 9 - 18 x = \color{red}9 \times 1 - \color{red}9 \times 2x = \color{red}9(1 - 2x)$
c)
$ 4 b - 16 a + 4 = \color{red}4 \times b - \color{red}4 \times 4 a + \color{red}4 \times 1 = \color{red}4 (b - 4a +1) $

12 - Equation with One Variable and Related Problems

Solutions
a)
Given the equation $ 3x - 2 = 4 $
Add $ 2 $ to both sides
\[ 3x - 2 + \color{red}2 = 4 + \color{red}2 \]
Simplify
\[ 3x = 6\]
Divide both sides by $3 $
\[ \displaystyle \frac{3x}{3} = \frac{6}{3} \]
Simplify
\[ x = 2 \]
b)
Given the equation $ 9 - 3 = - x + 5 $
Simplify the left side
\[ 6 = - x + 5 \]
Add $ -5 $ to both sides
\[ 6 + \color{red}{-5} = - x + 5 + \color{red}{-5} \]
Simplify
\[ 1 = - x \]
Multiply both sides by $ -1 $
\[ 1 (-1) = - x (-1) \]
Simplify
\[ -1 = x \]
c)
Given $ \displaystyle \frac{x}{3} = - 7 $
Multiply both sides by $ 3 $
\[ \displaystyle \frac{x}{3} \times \color{red}{3} = - 7 \times \color{red}{3} \]
Simplify
\[ x = - 21 \]
d)
Given $ 4 \left(x + \displaystyle \frac{1}{4} \right) = -15$
Expand the brackets
\[ 4 x + 4 \times \displaystyle \frac{1}{4} = - 15 \]
Simplify
\[ 4 x + 1 = - 15 \]
Add $ -1 $ to both sides
\[ 4 x + 1 \color{red}{-1} = - 15 \color{red}{-1} \]
Simplify
\[ 4 x = - 16 \]
Divide both sides by $ 4 $
\[ \displaystyle \frac{4x}{4} = \frac{-16}{4} \]
Simplify
\[ x = - 4 \]
e)
Given $ \displaystyle \frac{x+2}{-3} = 3 $
Multiply both sides by $ -3 $
\[ \displaystyle \frac{x+2}{-3} \times \color{red}{(-3)} = 3 \color{red}{(-3)} \]
Simplify
\[ x + 2 = - 9 \]
Add $ -2 $ to both sides and simplify
\[ x = - 11 \]
f)
$ 2(x-1) = 3(x+2) $
Expand the brackets
\[ 2x - 2 = 3x + 6 \]
Add $ -6 $ to both sides
\[ 2x - 2 + \color{red}{(-6 )} = 3x + 6 + \color{red}{(-6 )} \]
Simplify
\[ 2x - 8 = 3x \]
Subtract $ 2 x $ from both sides
\[ 2x - 8 \color{red}{-2x} = 3x \color{red}{-2x} \]
Simplify
\[ - 8 = x \]
g)
Given $\displaystyle x - 2 \frac{1}{4} = 3 $
Add the mixed number $ 2 \frac{1}{4} $ to both sides
\[\displaystyle x - 2 \frac{1}{4} \color{red}{ + 2 \frac{1}{4}} = 3 \color{red}{ + 2 \frac{1}{4}} \]
Simplify
\[\displaystyle x = 5 \frac{1}{4} \]
The perimeter of a rectangular garden is 340 m and its length is 120 m. Let $ x $ be the width of the garden.
a)
Formula: Perimeter $ = 2 \times length + 2 \times width $
Substitute the perimeter by 340, the length by 120 and the width by $ x $ \[ 340 = 2 \times 120 + 2 \times x \] Simplify \[ 340 = 240 + 2 x \]
b)
Solve the equation in part a)
\[ x = 50 \]
c)
Check answer
Perimeter = $ 2 \times length + 2 \times width $
Substitute the length and the width ( $ x = 50$ ) found above
Perimeter = \[ 2 \times 120 + 2 \times 50 = 340 \]
as given in the problem.

13 - Inequality with One Variable

Solutions
The three inequalities are represented the number lines below in red. A closed (red) circle means that the value is included. An open (red) circle means that the value is excluded
a), b) and c)
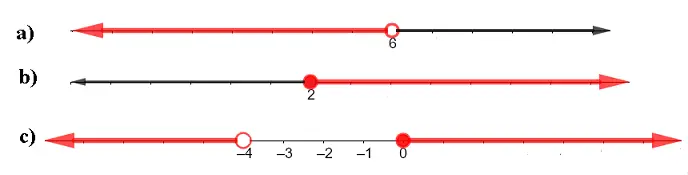
a) Given $ 4x - 2 \gt 18 $
Add $ 2 $ to both sides of the inequality \[ 4x - 2 \color{red}{+2} \gt 18 \color{red}{+2} \] Simplify \[ 4x \gt 20 \] Divide both sides by $ 4 $ \[ \displaystyle \frac{4 x}{4} \gt \frac{20}{4} \] Simplify to obtain the solution to the given inequality \[ x \gt 5 \]
b)
$ 2(x + 3) \le 6 $
Expand the brackets on the left side \[ 2 x + 6 \le 6 \] Subtract $ 6 $ from both sides of the inequality \[ 2 x + 6 \color{red}{-6} \le 6 \color{red}{-6} \] Simplify \[ 2 x \le 0 \] Divide both sides by $ 2 $ \[ \displaystyle \frac{2 x}{2} \le \frac{0}{2} \] Simplify to obtain the solution solution to the given inequality \[ x \le 0 \]

14 - Two-Dimensional Figures

Solutions
We are given the measures of two angles; let $ x $ be the measure of the third angle and the sum of the three angles of a triangle is equal to $ 180^{\circ} $, hence \[ 36^{^{\circ}} + 54^{^{\circ}} + x = 180^{\circ} \] Simplify the left side \[ 90^{^{\circ}} + x = 180^{\circ} \] Solve for $ x $ to obtain \[ x = 90^{^{\circ}} \] Hence the given triangle is a right triangle and b) is true.
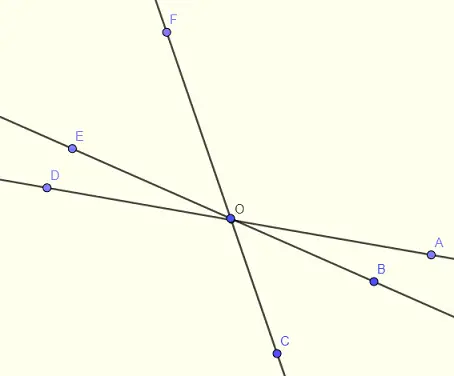
Angle $ \angle AOC $ is a straight angle and therefore angles $ \angle AOB $ are $ \angle COB $ are supplementary angles and their sum is equal to $ 180^{\circ} $. Hence
\[ \angle AOB + 27^{\circ} = 180^{\circ} \]
Solve for $ \angle AOB $ to obtain
$ \angle AOB = 153^{\circ} $
List of the pairs of vertical angles in the figure below are:
$ \angle AOB \; \text{and} \; \angle DOE \quad $ , $ \angle BOC \; \text{and} \; \angle EOF \quad $ , $ \angle COD \; \text{and} \; \angle FOA $
$ \angle FOB \; \text{and} \; \angle COE \quad $ , $ \angle AOC \; \text{and} \; \angle DOF \quad $ , $ \angle BOD \; \text{and} \; \angle EOA $
a) Hexagon : 6 sides b) Pentagon : 5 sides c) Octagon : 8 sides
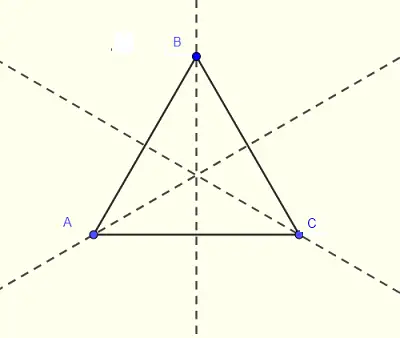
An equilateral triangle has 3 lines of symmetry as shown below.

15 - Perimeter and Area of Planar Figures

Solutions
$ \text{radius} = \displaystyle \frac{\text{diameter}}{ 2} = \frac{20 \; cm}{2} = 10 \; cm $
$ \text{Area} = 3.14 \times \text{radius} \times \text{radius} = 3.14 \times 10 \times 10 = 314 \; cm^2$
Perimeter of rectangle = $ 2 \times length + 2 \times width $
Substitute the length and the width by the given values Perimeter = $ 2 \times 10 + 2 \times 8 = 36 \text{ inches} $
Area of triangle = $ \frac{1}{2} \times height \times base $
Substitute the height and the base by the given values
Area of triangle = $ \frac{1}{2} \times 10 \times 5 = 25 \; cm^2 $
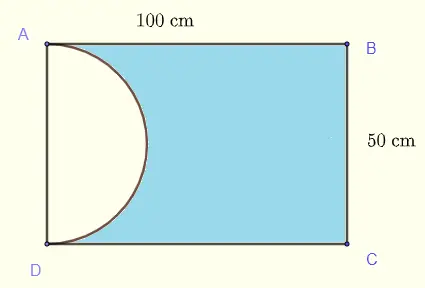
To find the shaded area, subtract the area of semicircle from the area of the main rectangle.
Shaded Area = area of rectangle - area of semicircle
$ \text{The radius of semicircle = diameter} / 2 = 50/2 = 25 \; cm $
Area of rectangle $ = length \times width = 100 \times 50 = 5000 cm^2 $
Area of semicircle $ = \frac{1}{2} \times 3.14 \times radius \times radius = \frac{1}{2} \times 3.14 \times 25 \times 25 = 981.25 \; cm^2 $
Shaded Area $ = 5000 \; cm^2 - 981.25 \; cm^2 = 4018.75 \; cm^2 $

16 - Data and Interpretation of Graphs

Solutions
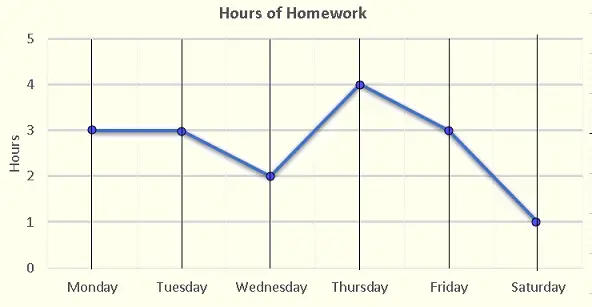
a) Saturday
b) Thursday
c) Total number of hours spent on homework $ = 3 + 3 + 2 + 4 + 3 + 1 = 16 \; hours $
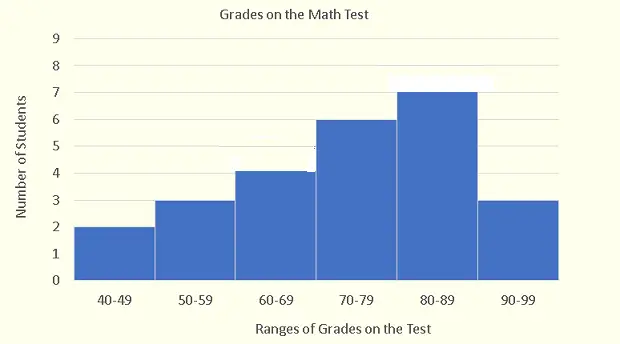
a) Number of students in this class is obtained by adding the number of students (in vertical axis) corresponding to each range. Number of students in this class $ = 2 + 3 + 4 + 6 + 7 + 3 = 25 $
b)
From 70 to 89, we have two ranges: 70 to 79 with 6 students and 80 to 89 with 7 students.
Hence $ 6 + 7 = 13 $ students scored between 70 and 89 inclusive.
c)
The number of students who failed are the ranges 40 to 49 and 50 to 59 and the number of students in each range are 2 and 3 respectively. Hence
The number of students who failed $ = 2 + 3 = 5$
The percent of the total number of students failed the test $ = \frac{5}{25} = 20\% $

17 - Statistics

Solutions
mean $ = \displaystyle \frac{9 + 4 + 3 + 2 + 3 + 2 + 3 + 1 + 9}{9} = 4 $
Arrange the given data from least to greatest values
$ \{ 1, 2, 2, 3, \color{red}3, 3, 4, 9, 9 \} $
The data value $ 3 $ has the highest number of occurrences and is therefore the mode
There are 9 data values and the data value $ 3 $ (red) is in the middle and is therefore the median
Let $ x $ be the score of Joel's fourth quiz. The mean is given as 90, hence
mean $ = \displaystyle \frac{78+95+92+x}{4} = 90 $
Simplify and write as an equation
$ \displaystyle \frac{265+x}{4} = 90 $
Multilply both sides of the equation by $ 4 $
$ \displaystyle \frac{265+x}{4} \times 4 = 90 \times 4 $
Simplify
$ 265 + x = 360 $
Hence
$ x = 360 - 265 = 95 $
Joel should score 95 on her fourth quiz so that the average of the 4 quizzes is 90.

18 - Counting Principle

Solutions
The number of ways the lunch may be served at this restaurant is $ 3 \times 5 \times 4 = 60 $
The first car dealership has $ 3 \times 4 \times 3 = 36 $ choices
The second car dealership has $ 2 \times 5 \times 4 = 40 $ choices
The second dealership has more choices.

19 - Probabilities

Solutions
A measure of a probability takes values between 0 and 1 inclusive. Hence b) -0.5 and c) 2 cannot be measures of probabilities
Flip a coin has 2 outcomes : head and tail
Selecting a card from five different cards has 5 outcomes.
Use the counting principle to find the number of outcomes when you flip a coin and select one of five different cards at random.
$ 2 \times 5 = 10 $ possible outcomes
a) The die has no face with a zero and therefore the probability of obtaining a zero is equal to zero.
b) one face out of 6 has 5 on it, the probability is equal to 1/6
c) Faces with 5 and 6 have number greater than 4. Therefore two faces out of 6 are greater than 4, probability is equal to 2/6 = 1/3.
From this experiment, 5 students picked the blue as their favorite color and therefore 15 picked a favorite color that is not blue.
Therefore, if a student is surveyed the probability that he/she will pick a color that is not blue is equal to 15/20 = 3/4.

Free Mathematics Tutorials

Solutions to Grade 7 Math Practice Test

1 - Integers

2 - Decimals

3 - Factors, Multiples and Divisibility of Numbers

4 - Fractions and Mixed Numbers

5 - Exponents

6 - Ratios and Rates and Related

7 - Proportionality and Related Problems

8 - Percent and Related Problems

9 - Convert Units of Measurement

10 - Evaluate Expressions

11 - Algebra

12 - Equation with One Variable and Related Problems

13 - Inequality with One Variable

14 - Two-Dimensional Figures

15 - Perimeter and Area of Planar Figures

16 - Data and Interpretation of Graphs

17 - Statistics

18 - Counting Principle

19 - Probabilities

More References and links