How do you find the area of a right triangle on a coordinate plane?

First, use the distance formula to find the lengths of the legs of the right triangle. Then, multiply the lengths of the two legs together and divide by 2, using the formula Area = 1/2 × base × height.

How do you use similar triangles to find missing side lengths?

When two triangles are similar, their corresponding sides are proportional. You can set up a ratio comparing the known side of one triangle to the corresponding known side of the other, and set it equal to the ratio of the side you are trying to find.

Grade 8 Triangle Problems: Practice Questions & Step-by-Step Solutions

Q: What is the Triangle Inequality Theorem?

The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be strictly greater than the length of the third side. If this condition is not met, the triangle cannot exist.

Triangle Inequality: The lengths of two sides of a triangle are 20 mm and 13 mm. Which of these lengths cannot represent the length of the third side?

35 mm
10 cm
20 mm
45 mm

Hint: The sum of any two sides of a triangle must be strictly greater than the third side.

View Step-by-Step Solution

In any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.

Given two sides with lengths 20 mm and 13 mm, their sum is:

$ 20 + 13 = 33 \text{ mm} $

Therefore, the third side length $ x $ must satisfy:

$ x \lt 33 \text{ mm} $

Now check the given options (remembering to convert cm to mm):

A) $ 35 \text{ mm} \gt 33 \text{ mm} $ (Not possible)
B) $ 10 \text{ cm} = 100 \text{ mm} \gt 33 \text{ mm} $ (Not possible)
C) $ 20 \text{ mm} \lt 33 \text{ mm} $ (Possible)
D) $ 45 \text{ mm} \gt 33 \text{ mm} $ (Not possible)

Answer: The lengths 35 mm, 10 cm, and 45 mm cannot represent the third side.

Isosceles Angles: Triangle ABC is an isosceles triangle. Find the size of angle ABC. $Isosceles triangle ABC with top angle 72 degrees$

View Step-by-Step Solution

The sum of the interior angles in any triangle is $ 180^\circ $:

$ 72^\circ + \angle ACB + \angle ABC = 180^\circ $

Because triangle ABC is isosceles (indicated by the tick marks on sides AB and AC), its base angles are equal:

$ \angle ACB = \angle ABC $

Let $ \angle ABC = x $. Then:

$ 72^\circ + 2x = 180^\circ $
$ 2x = 180^\circ - 72^\circ = 108^\circ $
$ x = 54^\circ $

Answer: $ \angle ABC = 54^\circ $

Equilateral Perimeter: The perimeter of an equilateral triangle is equal to 210 cm. What is the length of one side of this triangle?

View Step-by-Step Solution

In an equilateral triangle, all three sides are equal in length. If the length of one side is $ x $, then the perimeter is:

$ 3x = 210 $
$ x = \dfrac{210}{3} $
$ x = 70 \text{ cm} $

Answer: The length of one side is 70 cm.

Pythagorean Algebra: Find $ x $ so that the triangle shown below is a right triangle. $Right triangle with legs 12x and 16x and hypotenuse 10$

View Step-by-Step Solution

Use the Pythagorean theorem ($ a^2 + b^2 = c^2 $):

$ (12x)^2 + (16x)^2 = 10^2 $
$ 144x^2 + 256x^2 = 100 $
$ 400x^2 = 100 $
$ x^2 = \dfrac{100}{400} = \dfrac{1}{4} $

Taking the positive square root (since a side length multiplier must be positive):

$ x = \dfrac{1}{2} $

Answer: $ x = 0.5 $

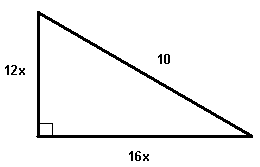Coordinate Reflection: What will be the vertices of the triangle obtained by a reflection across the x-axis of the triangle defined by the vertices (1, 2), (2, -3), and (4, -1)?

View Step-by-Step Solution

When a point $ (x, y) $ is reflected across the x-axis, its horizontal position stays the same, but its vertical position changes sign. The rule is $ (x, y) \to (x, -y) $.

Applying this rule to each vertex:

$ (1, 2) \to $ $ (1, -2) $
$ (2, -3) \to $ $ (2, 3) $
$ (4, -1) \to $ $ (4, 1) $

Similar Triangles: The two triangles shown below are similar. Find the length of the hypotenuse of the larger triangle. $Two similar right triangles. Small triangle has legs 6 and 8. Large triangle has corresponding leg 15.$

View Step-by-Step Solution

First, find the hypotenuse $ h $ of the smaller right triangle using the Pythagorean theorem:

$ h^2 = 8^2 + 6^2 $
$ h^2 = 64 + 36 = 100 $
$ h = 10 $

In similar triangles, corresponding sides are proportional. Let $ H $ be the hypotenuse of the larger triangle. The ratio of the corresponding legs is equal to the ratio of the hypotenuses:

$ \dfrac{6}{15} = \dfrac{10}{H} $

Cross-multiply to solve for $ H $:

$ 6 H = 150 $
$ H = \dfrac{150}{6} $
$ H = 25 $

Answer: The length of the hypotenuse of the larger triangle is 18.75 units.

Real-World Application: A 13-foot ladder is leaning against a vertical wall. The lowest point of the ladder is 4 feet from the wall. What is the height of the point where the ladder touches the wall? (Round your answer to the nearest tenth of a foot).

View Step-by-Step Solution

The ladder, the wall, and the ground form a right triangle where the ladder is the hypotenuse ($ c = 13 $) and the ground distance is one leg ($ a = 4 $). Let the height of the wall be $ x $.

Use the Pythagorean theorem:

$ x^2 + 4^2 = 13^2 $
$ x^2 + 16 = 169 $
$ x^2 = 169 - 16 = 153 $
$ x = \sqrt{153} $

Calculating the square root:

$ x \approx 12.369 $

Answer: The ladder touches the wall at approximately 12.4 feet.

Special Right Triangles: The length of the hypotenuse of a right triangle is 40 cm. The size of one of its angles is 45 degrees. What are the exact lengths of the other two sides of the triangle?

View Step-by-Step Solution

In a right triangle, if one angle is $ 45^\circ $, the other acute angle must also be $ 180^\circ - 90^\circ - 45^\circ = 45^\circ $. Because the base angles are equal, the triangle is isosceles, meaning both legs have the exact same length. Let the length of each leg be $ x $.

Using the Pythagorean theorem:

$ x^2 + x^2 = 40^2 $
$ 2x^2 = 1600 $
$ x^2 = 800 $
$ x = \sqrt{800} = \sqrt{400 \times 2} = 20\sqrt{2} $

Answer: The exact length of each of the other two sides is $ 20\sqrt{2} $ cm.

Isosceles Perimeter: Triangle ABC is an isosceles triangle. The length of the base is 20 meters and the corresponding height is 24 meters. Find the perimeter of ABC.

View Step-by-Step Solution

The height of an isosceles triangle bisects the base, splitting it into two equal segments of 10 meters each, and forms two identical right triangles.

$Isosceles triangle divided into two right triangles by its height$

Use the Pythagorean theorem to find the length $ x $ of the slanted sides (the hypotenuse of the right triangles):

$ x^2 = 24^2 + 10^2 $
$ x^2 = 576 + 100 = 676 $
$ x = \sqrt{676} = 26 \text{ meters} $

The perimeter of the triangle is the sum of the base and the two identical slanted sides:

$ \text{Perimeter} = 20 + 26 + 26 = 72 $

Answer: The perimeter is 72 meters.

Area Algebra: A triangle has an area of 90 square cm. Find the length of the base if the base is 3 cm more than the height.

View Step-by-Step Solution

Let $ h $ be the height. The base $ b $ is given as $ b = h + 3 $.

Using the area formula $ A = \dfrac{1}{2} \times b \times h $:

$ 90 = \dfrac{1}{2}(h + 3)h $

Multiply both sides by 2 to clear the fraction:

$ 180 = h(h + 3) $
$ h^2 + 3h - 180 = 0 $

Factor the quadratic equation:

$ (h + 15)(h - 12) = 0 $

Since height must be a positive measurement, $ h = 12 $.

Calculate the base:

$ b = 12 + 3 = 15 $

Answer: The length of the base is 15 cm.

Perimeter Algebra: The perimeter of a triangle is 74 inches. The length of the first side is twice the length of the second side. The third side is 4 inches more than the first side. Find the length of each side.

View Step-by-Step Solution

Let $ x $ be the length of the second side. We can define the other sides based on $ x $:

First side = $ 2x $
Second side = $ x $
Third side = $ 2x + 4 $

The perimeter is the sum of all three sides:

$ 2x + x + (2x + 4) = 74 $
$ 5x + 4 = 74 $
$ 5x = 70 $
$ x = 14 $

Now, substitute $ x = 14 $ back into the side expressions:

First side: $ 2(14) = 28 \text{ inches} $
Second side: $ 14 \text{ inches} $
Third side: $ 28 + 4 = 32 \text{ inches} $

Answer: The side lengths are 28, 14, and 32 inches.

Coordinate Area: Determine the area of the triangle enclosed by the lines $ y = -4 $, $ x = 1 $, and $ y = -2x + 8 $.

View Step-by-Step Solution

The triangle's vertices are the points where these three lines intersect. Let's find points A, B, and C.

$Triangle graphed on coordinate plane intersecting lines$

Find Point A (Intersection of $ x = 1 $ and $ y = -2x + 8 $):

Substitute $ x = 1 $ into the equation: $ y = -2(1) + 8 = 6 $
A = (1, 6)

Find Point C (Intersection of $ y = -4 $ and $ y = -2x + 8 $):

Substitute $ y = -4 $ into the equation: $ -4 = -2x + 8 \implies -2x = -12 \implies x = 6 $
C = (6, -4)

Find Point D (Intersection of $ x = 1 $ and $ y = -4 $):

D = (1, -4)

Because the lines $ x = 1 $ (vertical) and $ y = -4 $ (horizontal) are perpendicular, this is a right triangle. The base and height are the straight vertical and horizontal distances:

Height (AB) = vertical distance from $ y = 6 $ to $ y = -4 $ = $ |6 - (-4)| = 10 $
Base (BC) = horizontal distance from $ x = 1 $ to $ x = 6 $ = $ |6 - 1| = 5 $

Calculate Area:

$ \text{Area} = \dfrac{1}{2} \times 5 \times 10 = 25 $

Answer: The area of the triangle is 25 square units.

Distance Formula: Show that the triangle with vertices A(-1,6), B(2,6), and C(2,2) is a right triangle and find its area.

View Step-by-Step Solution

Calculate the squared length of each side using the distance formula $ d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 $:

$ AB^2 = (2 - (-1))^2 + (6 - 6)^2 = 3^2 + 0^2 = 9 $
$ BC^2 = (2 - 2)^2 + (2 - 6)^2 = 0^2 + (-4)^2 = 16 $
$ CA^2 = (-1 - 2)^2 + (6 - 2)^2 = (-3)^2 + 4^2 = 9 + 16 = 25 $

Check if the Pythagorean theorem ($ a^2 + b^2 = c^2 $) applies:

$ AB^2 + BC^2 = 9 + 16 = 25 $
Since $ AB^2 + BC^2 = CA^2 $ (25 = 25), the triangle is a right triangle with the hypotenuse being side CA.

Because it is a right triangle, AB and BC are the base and height. The side lengths are $ AB = \sqrt{9} = 3 $ and $ BC = \sqrt{16} = 4 $.

Calculate Area:

$ \text{Area} = \dfrac{1}{2} \times 3 \times 4 = 6 $

Answer: The triangle is a right triangle with an area of 6 square units.

Grade 8 Problems and Questions on Triangles

Practice Questions

Links and References