Geometry Problems and Questions with Answers for Grade 9

Grade 9 geometry problems and questions with answers are presented. These problems deal with finding the areas and perimeters of triangles, rectangles, parallelograms, squares and other shapes. Several problems on finding angles are also included. Some of these problems are challenging and need a good understanding of the problem before attempting to find a solution.



  1. Angles A and B are complementary and the measure of angle A is twice the measure of angle B. Find the measures of angles A and B,

  2. ABCD is a parallelogram such that AB is parallel to DC and DA parallel to CB. The length of side AB is 20 cm. E is a point between A and B such that the length of AE is 3 cm. F is a point between points D and C. Find the length of DF such that the segment EF divide the parallelogram in two regions with equal areas.

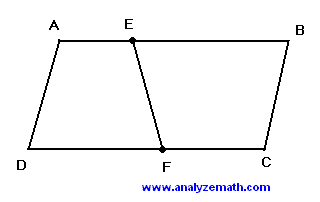    geometry problem 2.

  3. Find the measure of angle A in the figure below.

    geometry problem 3.

  4. ABC is a right triangle. AM is perpendicular to BC. The size of angle ABC is equal to 55 degrees. Find the size of angle MAC.

    geometry problem 4.

  5. Find the size of angle MBD in the figure below.

    geometry problem 5.

  6. The size of angle AOB is equal to 132 degrees and the size of angle COD is equal to 141 degrees. Find the size of angle DOB.

    geometry problem 6.

  7. Find the size of angle x in the figure.

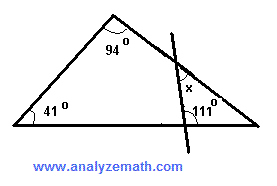    geometry problem 7.

  8. The rectangle below is made up of 12 congruent (same size) squares. Find the perimeter of the rectangle if the area of the rectangle is equal to 432 square cm.

    geometry problem 8.

  9. ABC is a right triangle with the size of angle ACB equal to 72 degrees. The lengths of the sides AM, MQ and QP are all equal. Find the measure of angle QPB.

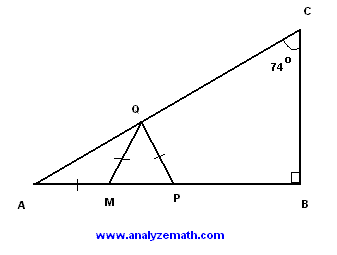    geometry problem 9.

  10. Find the area of the given shape.

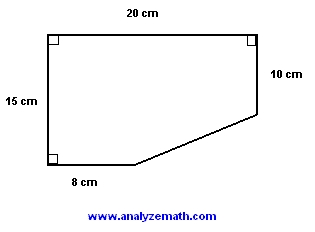    geometry problem 10.

  11. Find the area of the shaded region.

    geometry problem 11.

  12. The vertices of the inscribed (inside) square bisect the sides of the second (outside) square. Find the ratio of the area of the outside square to the area of the inscribed square.

    geometry problem 12.

Answers to the Above Questions

  1. measure of A = 60 degrees, measure of B = 30 degrees
  2. length of DF = 17 cm
  3. measure of A = 87 degrees
  4. size of angle MAC = 55 degrees
  5. size of angle MBD = 72 degrees
  6. size of angle DOB = 93 degrees
  7. size of angle x = 24 degrees
  8. perimeter of large rectangle = 84 cm
  9. measure of angle QPB = 144 degrees
  10. area of given shape = 270 square cm
  11. area of shaded region = 208 square cm
  12. ratio of area of outside square to area of inscribed square = 2:1

More Middle School Math (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers

More Primary Math (Grades 4 and 5) with Free Questions and Problems With Answers

Author - e-mail

Home Page
Updated: 4 April 2009 (A Dendane)