Convert Polar and Rectangular Coordinates

Rectangular coordinates \( (x, y) \) and polar coordinates \( (R, t) \) are related by the following formulas.

These formulas allow us to convert points from one coordinate system to the other.

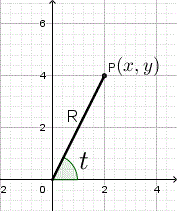
To find the polar angle \( t \), you must take into account the signs of \( x \) and \( y \), which determine the correct quadrant.

The angle \( t \) is usually taken in the interval \[ [0, 2\pi) \quad \text{or} \quad [0^\circ, 360^\circ) \]

Examples on Converting Polar and Rectangular Coordinates

Example 1

Convert the polar coordinates \( (5, 2.01) \) and \( (0.2, 53^\circ) \) to rectangular coordinates, rounding to three decimal places.

Solution to Example 1

• First point: \( (5, 2.01) \)
  Here \( R = 5 \) and \( t = 2.01 \) radians. Set the calculator to radians. \[ x = R \cos t = 5 \cos(2.01) = -2.126 \] \[ y = R \sin t = 5 \sin(2.01) = 4.525 \]
• Second point: \( (0.2, 53^\circ) \)
  Here \( R = 0.2 \) and \( t = 53^\circ \). Set the calculator to degrees. \[ x = R \cos t = 0.2 \cos(53^\circ) = 0.120 \] \[ y = R \sin t = 0.2 \sin(53^\circ) = 0.160 \]

Example 2

Convert the rectangular coordinates \( (1, 1) \) and \( (-2, -4) \) to polar coordinates, rounding to three decimal places. Express the polar angle \( t \) in both radians and degrees.

Solution to Example 2

• For the point \( (1, 1) \), compute \( R \): \[ R = \sqrt{x^2 + y^2} = \sqrt{1^2 + 1^2} = \sqrt{2} \]
• Compute \( \tan t \): \[ \tan t = \frac{y}{x} = \frac{1}{1} = 1 \]
• Using the inverse tangent: \[ t = \frac{\pi}{4} \quad \text{or} \quad 45^\circ \]
• The polar form of \( (1, 1) \) is: \[ (\sqrt{2}, \tfrac{\pi}{4}) \quad \text{or} \quad (\sqrt{2}, 45^\circ) \]
• For the point \( (-2, -4) \), compute \( R \): \[ R = \sqrt{(-2)^2 + (-4)^2} = \sqrt{20} = 2\sqrt{5} \]
• Compute \( \tan t \): \[ \tan t = \frac{-4}{-2} = 2 \]
• Using the inverse tangent: \[ t = 1.107 \text{ radians} \quad \text{or} \quad 63.435^\circ \]
• Since both \( x \) and \( y \) are negative, the point lies in quadrant III. Add \( \pi \) (or \( 180^\circ \)) to get the correct angle: \[ t = 4.249 \text{ radians} \quad \text{or} \quad 243.435^\circ \]
• The polar form of \( (-2, -4) \) is: \[ (2\sqrt{5}, 4.249) \quad \text{or} \quad (2\sqrt{5}, 243.435^\circ) \]

More References on Polar Coordinates

Convert Polar to Rectangular Coordinates Calculator

Polar Coordinates – Geometry Overview

Trigonometry Tutorials and Practice Problems