Polar Coordinates and Polar Equations

This page presents a clear introduction to polar coordinates and polar equations, with detailed explanations, worked examples, and graphical illustrations.

Review of Cartesian (Rectangular) Coordinates

We begin by reviewing the Cartesian (rectangular) coordinate system. Let point \( A \) lie in the \( xy \)-plane. In Cartesian coordinates, the point \( A \) is represented by an ordered pair \( (x, y) \), where:

\( x \) is the signed distance from the \( y \)-axis
\( y \) is the signed distance from the \( x \)-axis

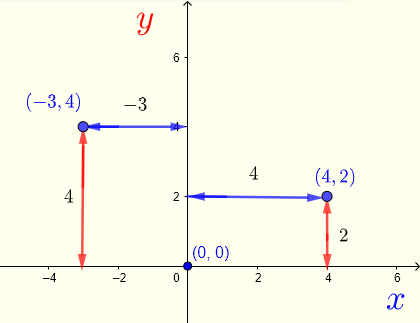
In the figure below, the points \( (x,y) = (4,2) \) and \( (x,y) = (-3,4) \) are shown.

Cartesian coordinates examples — Fig. 1 – Cartesian Coordinates

Polar Coordinate System and Definitions

In the polar coordinate system, a point is represented by the ordered pair \( (r, \theta) \), where:

\( r \) is the distance from the origin (called the pole)
\( \theta \) is the angle measured from the polar axis

The quantity \( r \) is called the radial coordinate, and \( \theta \) is the angular coordinate.

For example, the points \[ (5, \tfrac{\pi}{3}) \quad \text{and} \quad (4, \pi) \] are shown in the figure below.

Polar coordinates examples — Fig. 2 – Polar Coordinates

By convention, the angle \( \theta \) is positive when measured counterclockwise and negative when measured clockwise.

Example 1

Plot the points given by their polar coordinates:

a) \( (2,0) \) b) \( (2,\tfrac{3\pi}{4}) \) c) \( (4,\tfrac{7\pi}{3}) \) d) \( (3,-\tfrac{5\pi}{4}) \)

Solution to Example 1

The points are plotted below.

Polar coordinates plotted points example 1 — Fig. 3 – Plots of Points in Example 1

Note: If the radial coordinate \( r \) remains the same and we add or subtract multiples of \( 2\pi \) to the angular coordinate, the same point is obtained.

That is, \[ (r,\theta), \quad (r,\theta + 2\pi), \quad (r,\theta - 4\pi), \dots \] all represent the same point.

Negative Values of the Radial Coordinate

The polar coordinate system allows the radial coordinate \( r \) to be negative. The points \[ (-r, \theta) \quad \text{and} \quad (r, \theta) \] lie on the same line through the pole and are the same distance \( |r| \) from the pole, but in opposite directions.

Thus, the coordinates \[ (-r, \theta) \quad \text{and} \quad (r, \theta + \pi) \] represent the same point.

Example 2

Plot the following pairs of points:

a) \( (-2,0) \) and \( (2,0) \)
b) \( (-2,\tfrac{3\pi}{4}) \) and \( (2,\tfrac{3\pi}{4}) \)
c) \( (-4,-\tfrac{\pi}{3}) \) and \( (4,-\tfrac{\pi}{3}) \)

Solution to Example 2

Polar coordinates with negative r — Fig. 4 – Effect of Negative Radial Coordinates

The Same Point with Different Polar Coordinates

Unlike Cartesian coordinates, polar coordinates are not unique. A single point can be represented in infinitely many ways.

For integers \( n \) and \( k \), the coordinates \[ (r,\theta), \quad (r,\theta + 2n\pi), \quad (-r,\theta + (2k+1)\pi) \] all represent the same point.

Relationships Between Polar and Cartesian Coordinates

Using trigonometry, the relationships between polar and Cartesian coordinates are:

\[ x = r\cos\theta, \qquad y = r\sin\theta \] \[ r^2 = x^2 + y^2, \qquad \theta = \arctan\!\left(\frac{y}{x}\right) \]

Relationship between Cartesian and polar coordinates — Fig. 5 – Polar–Cartesian Coordinate Relationships

Polar Equations and Curves

A polar equation has the form \( f(r,\theta) = 0 \). Its graph consists of all points \( (r,\theta) \) satisfying the equation.

Example 4

Sketch the graph of the polar equation

\[ r - 3\sin\theta = 0 \]

Solution to Example 4

Solving for \( r \), we obtain:

\[ r = 3\sin\theta \]

A table of values is shown below.

\( \theta \)	\( r = 3\sin\theta \)
\( 0 \)	\( 0 \)
\( \tfrac{\pi}{6} \)	\( \tfrac{3}{2} \)
\( \tfrac{\pi}{4} \)	\( \tfrac{3}{\sqrt{2}} \)
\( \tfrac{\pi}{3} \)	\( \tfrac{3\sqrt{3}}{2} \)
\( \tfrac{\pi}{2} \)	\( 3 \)
\( \tfrac{2\pi}{3} \)	\( \tfrac{3\sqrt{3}}{2} \)
\( \tfrac{3\pi}{4} \)	\( \tfrac{3}{\sqrt{2}} \)
\( \tfrac{5\pi}{6} \)	\( \tfrac{3}{2} \)
\( \pi \)	\( 0 \)

Graph of r = 3 sin theta — Fig. 6 – Graph of \( r = 3\sin\theta \)

Converting to Cartesian coordinates:

\[ r - 3\sin\theta = 0 \] \[ r - 3\frac{y}{r} = 0 \] \[ r^2 - 3y = 0 \] \[ x^2 + y^2 - 3y = 0 \]

Completing the square correctly:

\[ x^2 + (y - 1.5)^2 = (1.5)^2 \]

This is a circle centered at \( (0, 1.5) \) with radius \( 1.5 \).