Solution
| When two dice are tossed, there are 6 * 6 = 36 possible outcomes. |
(1,1) , (1,2) , (1,3) , (1,4) , (1,5) , (1,6)
(2,1) , (2,2) , (2,3) , (2,4) , (2,5) , (2,6) (3,1) , (3,2) , (3,3) , (3,4) , (3,5) , (3,6) (4,1) , (4,2) , (4,3) , (4,4) , (4,5) , (4,6) (5,1) , (5,2) , (5,3) , (5,4) , (5,5) , (5,6) (6,1) , (6,2) , (6,3) , (6,4) , (6,5) , (6,6) |
| The outcomes that give a sum of 3 or less are | (1,1) , (1 , 2) and (2,1) |
| There are | 36 - 3 = 33 possible outcomes that give a sum that is greater than 3 |
| The probability that the sum of the two dice is greater than 3 | 33 / 36 = 11 / 12 |
Solution
| The slope of the line through (2,5) and (4,6) is given by | (6 - 5) / (4 - 2) = 1 / 2 |
| The slope of the line through (4,6) and (7,k) is given by | (k - 6) / (7 - 4) = (k - 6) / 3 |
| The three points are on the same line and therefore the slopes found above must be equal | 1 / 2 = (k - 6) / 3 |
| Solve the above equation for k to find | k = 15/2 |
Solution
| To find points of intersection of the graphs of y = x2 - 2 x + 7 and y = k x + 5, we need to solve the system of the two equations | y = x2 - 2 x + 7 y = k x + 5 |
| Eliminate y between the two equations to obtain | x2 - 2 x + 7 = k x + 5 |
| The above equation may be written as | x2 - x(2 + k) + 2 = 0 |
| This is a quadratic equation which may have no solutions meaning that the two graphs have no points of intersection, two solutions which means the two graphs have two points of intersection or one solution which means the two graphs are tangent to each other. A quadratic equation have one solution if its discriminant is equal to 0. Hence | (2 + k)2 - 4(1)(2) = 0 |
| Solve for k and select the negative solution | k = - 2 - 2 √2 |
 .
.
Solution
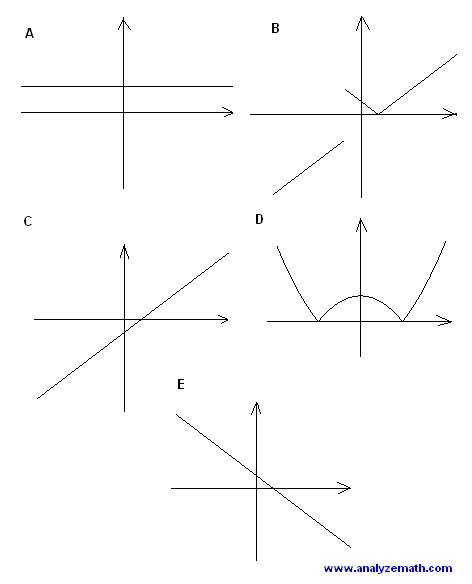
Function f(x) = |4 - x2| / (x + 2) is undefined for x = -2 and the only graph that is undefined for x negative is graph B.
 .
.
Solution
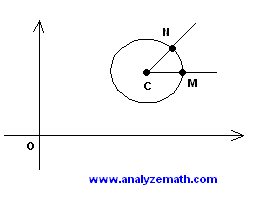
| One way to find the coordinates of N is to find the components of vector ON. | Vector ON = Vector OC + Vector CN |
| The equation of the circle gives the coordinates of the center C which are | C (3 , 2) |
| The components of vector OC are | < 3 , 2 > |
| Distance CN is equal to the radius of the circle which is 1. Points C and M have the same y coordinates and therefore CM is parallel to the x axis, hence the components of vector CN are given by | <1 . cos(30o) , 1 . sin(30o)> = < √3 / 2 , 1 / 2> |
| Hence the components of vector ON are given by | < 3 , 2 > + < (1 / 2)√3 , 1 / 2 > = < 3 + √3 / 2 , 5/2 > |
| The coordinates of point N are given by | ( 3 + √3 / 2 , 5/2 ) |
Solution
| We first find w = -u - 2v as follows |
w = -u - 2v = - < 2 , 0 >
-2 < - 3 , 1 > = < - 2 , 0> + < 6 , - 2 > = < 4 , - 2 > |
| The length of W is given by | √(42 + (-2)2) = 2 √5 |
Solution
| Let us find the center and radius of the circle | The equation of the circle is in standard form and its center has coordinates (1 , 2) and its radius is equal to 2. |
| The distance between the center of the circle and point (-2, -2) is given by | √( (-2 -1)2 + (-2 -2)2 ) = 5 |
| Point (-2,-2) is outside the circle. The shortest distance between point (-2,-2) and a point on the circle is given by | 5 - 2 = 3 |
Solution
If x increases indefinitely, 2 / (x + 2) will approach 0 and - (x + 3) / (x + 4) will approach - 1. If x decreases indefinitely, 2 / (x + 2) will approach 0 and - (x + 3) / (x + 4) will approach - 1. Hence the equation of the horizontal asymptote is y = - 1.
Solution
| Let us find the slope of the line with equation x + 3y = 2 |
3y = - x + 2 y = -(1 / 3)x + 2/3 slope = -1 / 3 |
| The slope of the line with equation -2x + ky = 5 is calculated as follows | k y = 2x + 5 y = (2 / k) x + 5 / k slope = 2 / k |
| For two lines to be perpendicular, the product of their slopes must be equal to - 1. Hence | (-1 / 3)*(2 / k) = -1 |
| Solve the above equation for k to find | k = 2 / 3 |
Solution
| (g o f) (x) is the composition of functions defined as follows | (g o f) (x) = g ( f (x) ) |
| Substitute f (x) by (x - 1) 2 |
(g o f) (x) = g ( f (x) ) = g( (x - 1) 2 ) = √(x - 1) 2 = | x - 1 | |
| NOTE THAT √ x 2 = | x | not x |
Solution
Remember that the domain of a function is the set of all values of x that make f(x) a real number. The given function has square roots which must be positive or zero because the square root of a negative number is not a real number. The expression in the denominator cannot be zero because we cannot divide by zero. Hence the two conditions to satisfy
1) (x2 - 1) > 0
2) (4 - x2) ≥ 0
Factor (x2 - 1) and solve the inequality 1)
(x - 1)(x + 1) > 0
The sign chart of (x - 1)(x + 1) is shown below
 .
.
[-1 , 0) U (0 , +1]
We now factor (4 - x2) and solve the inequality 2)
(2 - x)(2 + x) ≥ 0
The sign chart of (2 - x)(2 + x) is shown below
 .
.
[-2 , 2]
For a given value of x to be in the domain of f it must satisfy both inequalities above which means the domain is the set of x values belonging to the intersection of the intervals [-1 , 0) U (0 , +1] and [-2 , 2] as shown below
 .
.
[-2, -1) U (1, 2]
Solution
| We first need to write the given equation in standard form by completing square | x 2 + y 2 - 8 y - 48 = 0 |
| Write the term (y 2 - 8 y) as a square plus a constant : add and subtract 16 | y 2 - 8 y = y 2 - 8 y
+ 16 - 16 = (y - 4) 2 - 16
|
| Substitute by in the given equation and write the equation of the circle in standard form | x 2 +
(y - 4) 2
- 16 -
48 = 0 or x 2 + (y - 4) 2 = 64 |
| Hence the radius R of the circle is equal to 8. The area is given | Pi R 2 = 64 Pi |
Solution
| The points of intersections of the parabola and the circle are solutions to both equations simultaneously and therefore to find these points we need to solve the system of equations defined by | y2 = x + 2 x2 + y2 = 4 |
| Substitute y2 by x + 2 in the second equation and rewrite the equation obtained in standard form | x2 + x + 2 = 4 x2 + x - 2 = 0 |
| Solve the quadratic equation obtained | x = 1 and x = -2 |
| We now substitute the values of x obtained in the equation y2 = x + 2 to find y | For x = 1 , and y2 = 1 + 2 = 3 y = + or - √3 for x = -2 , and y2 = -2 + 2 = 0 hence y = 0 |
| The y coordinates of the points of intersection are | - √3 , 0 and √3 |
Solution
| The zeros of function f are found by solving the equation | 1/2 - sin(3x + Pi/3) = 0 |
| Rearrange the equation to obtain | sin(3x + Pi/3) = 1 / 2 |
| In order to solve the trigonometric equation above, we need to solve the two equations below. Note that because sine functions are periodic, there is an infinite number of solutions. | 3x + Pi/3 = Pi / 6 + 2 k Pi and 3x + Pi/3 = 5 Pi / 6 + 2 k Pi for k any integer |
| We now solve the above equations. | First equation: 3x + Pi/3 = Pi / 6 + 2 k Pi
3x = - Pi / 6 + 2 k Pi x = - Pi / 18 + 2 k Pi / 3 Second equation: 3x + Pi/3 = 5 Pi / 6 + 2 k Pi 3x = Pi / 2 + 2 k Pi x = Pi / 6 + 2 K Pi / 3 |
| We now need to find the smallest positive solution. | For k = 0 we have two solutions: x = - Pi / 6 and Pi / 6 and hence the smallest zero is equal to Pi / 6 |
I) x2 + 1
II) x2 - 1
III) x2 - 4x + 3
Solution
| We first use the factors to write polynomial P as follows | P(x) = k (x - 1)(x - 3)(x + 1) , k is a nonzero real number |
| Other possible factors of P(x) are | (x - 1)(x - 3) = x2 - 4 x + 3
(x - 1)(x + 1) = x2 - 1 and (x - 3)(x + 1) = x2 - 2x -3 |
| Of those listed in I, II and III, II and III are also factors of P(x). |
Solution
| Let V1 be the volume of the small cylinder and V2 the volume of the large cylinder where | V1 = (52 Pi) * 20 V2 = (102 Pi) * 20
|
| The volume V of the region bewteen the two cylinders in the difference between the two volumes | V = V2 - V1 = 1500 Pi cm3
|
Solution
| The standard deviation involves the square root of the sum of(xi - m)2 where xi are the data values and m is the mean. If each data value is multiplied by k then the mean will be k times. Hence the new standard deviation will involve the square root of the sum of (k xi - k m)2 | and therefore the new standard deviation will be k times the old standard deviation. In this case k = 4 and the old standard deviation is one. The standard deviation after multiplication will be equal to 4.
Solution
When cut open along the slant height H and flattened, the cone becomes a sector of a circle as shown in the figure below right and the perimeter of the base of the cone is equal to arc length of the sector shown on the right. The perimeter P of the base of the cone is given by:
 .
.
P = 2 Pi r = 2 Pi 6 = 12 Pi
The slanted height H is calculated using Pythagora theorem
H = √(r2 + h2) = √(62 + 82) = 10
The arc length of S the sector is given by
S = H * t = 10 t , where t is the sector angle to find.
S = P gives 12 Pi = 10 t
t = 1.2 Pi = 216 degrees.
Solution
We first express cot(2x) as follows
cot(2x) = 1 / tan(2x) = ( 1 - tan2 ) / ( 2 tan(x) )
We now need to find tan(x) using the identity
tan(x) = sin(x) / cos(x)
We know the value of sin(x), we need to find the value of cos(x) using the identity sin2(x) + cos2(x) = 1 as follows
cos2(x) = 1 - sin2(x)
Solving the above for cos(x), we obtain two solutions
cos(x) = √(1 - sin2(x)) and cos(x) = - √(1 - sin2(x))
Angle x satisfies the condition Pi ≤ x ≤ 3Pi/2 for which cos(x) is negative. Hence
cos(x) = - √(1 - sin2(x))
We now substitute and determine cot(2 x) as follows
cos(x) = - √(1 - (-1/3)2)
= - √(8/9) = - 2 √2 / 3
tan(x) = sin(x) / cos(x) = (-1/3) / ( - 2 √2 / 3 ) = 1 / 2 √2
cot(2 x) = ( 1 - tan2 ) / ( 2 tan(x) ) = ( 1 - 1/8 ) / ( 1 / √2 ) = 7 √ 2 / 8 = 7 / ( 4 √ 2 )
I) f(x) = - x
II) f(x) = √x
III) f(x) = - 1/x
Solution
Let us find the inverse of f(x) = - x
y = - x , write given function as equation
x = - y , change x to y and y to x
y = - x = f -1(x) , solve for y to find inverse
The given function satisfies f(x) = f -1(x).
Let us find the inverse of f(x) = √x
y = √x
x = √y
y = x2 and is different from f(x) = √x
The given function does not satisfy the condition f(x) = f -1(x)
Let us find the inverse of f(x) = - 1/x
y = - 1/x
x = - 1/y
x y = - 1
y = - 1/x = f -1(x)
The given function satisfies the condition f(x) = f -1(x)
 .
.
Solution
A function of the form y = | f(x) | take positive values or zero. The graphs in A) and B) have negative values and therefore neither can be the graph of y = | f(x) |. In fact B) is not the graph of a function. Also f(x) is undefined at x = 2 and also has a vertical asymptote at x = 2. The only graph that seems to have a vertical asymptote at x = 2 is graph C) and is therefore the closet to the graph of | f(x) |.
Solution
The sum of all three angles in a triangle is equal to 1800. Hence
A + B + C = 1800
or A + B = 1800 - C
The above gives
cos( 1800 - C ) = cos ( A + B )
Use trigonometry formula to rewrite above as
cos( 1800 ) cos( C ) + sin( 1800 ) sin( C ) = cos (A) cos (B ) - sin( A ) sin( B )
Simplify and rewrite the above as
cos ( C ) = sin( A ) sin( B ) - cos( A ) cos( B )
Given that sin(A) = 1/5 and cos(B) = 2/7, We now need to find cos (A) and sin (B) using identities as follows:
cos (A) = √(1 - (1/5)2) = √24 / 5
sin (B) = √(1 - (2/7)2) = √45 / 7
Substitute the values of sin(A), sin(B), cos(A) and cos(B) into cos ( C ) = sin( A ) sin( B ) - cos( A ) cos( B ) we obtain
cos(C) = (√45 - 2√24) / 35
| 100 |
| ∑ (3 + k) |
| k=1 |
Solution
Rewriting the sum explicitly, we have
| 100 |
| ∑ (3 + k) = 4 + 5 + 6 +...+ 103 |
| k=1 |
The terms in the sum are those of an arithmetic sequence with common difference 1. Hence the sum is equal to the average the first term and the last term multiplied by the number of terms which is 100. Hence
| 100 |
| ∑ (3 + k) = 100*(4 + 103)/2 = 5350 |
| k=1 |
Solution
Let r be the common ratio of the geometric sequence. Hence the relationship between the first and second term and the second and third term are as follows
x / (x + 1) = r x and 3x / [(x + 1)(x + 2)] = r x / (x + 1)
Solve both equations above for x to obtain
r = 1 / (x + 1) and r = 3 / (x + 2)
r is constant, hence
1 / (x + 1) = 3 / (x + 2)
Solve the above for x to obtain
x = -1 / 2
A) always increases
B) always decreases
C) increases then decreases
D) decreases then increases
E) stay constant
Solution
As x changes g(x) = |sin(2x)| takes either positive values or zero.
For x = Pi / 4, g(Pi/4) = | sin(2 Pi/4) | = 1
For x = Pi / 2, g(Pi/2) = | sin(2 Pi/2) | = 0
For x = 3 Pi / 4, g(3 Pi/4) = | sin(3 Pi/2) | = 1
As x increases from Pi/4 to 3Pi/4, |sin(2x)| decreases then increases.
Solution
Let P(x) = a x3 + b x2 + c x + d. According to the remainder theorem, the remainder r when dividing P(x) by x - 2 is equal to P(2). Hence
r = P(2) = a 23 + b 22 + 2 c + d
= 8a + 4b + 2c + d
Solution
Let C(n,r) be the number of samples of r elements to be selected from a set of n elements (combinations). Then
C(n,r) = n! / r! (n - r)!
The committee has a total of 6 members. If the number of males and females in this committee are equal then the committee has 3 males and 3 females. There are C(5,3) ways to select 3 males from 5, C(8,3) ways to select 3 females from 8 and C(13,6) ways to select 6 persons from 13. The probability is equal to
P = C(5,3)*C(8,3) / C(13,6) = (5! / 3!2!)*(8! / 3!5!) / (13! / 6!7!) = 140 / 429
Solution
The absolute value is either positive or zero. Hence
|x - 2| ≥ 0
Multiply both sides of the inequality by -1 and reverse the symbol of inequality to obtain
- |x - 2| ≤ 0
Subtract 3 from both sides of the inequality to obtain
- |x - 2| - 3 ≤ - 3
The right side of the above inequality is equal to f(x). Hence the inequality gives
f(x) ≤ - 3
The above inequality states that the range of y = f(x) is given by
y ≤ -3
Solution
The period P is defined for sine and cosine functions of the form A sin (Bx + C) + D or A cos (BX + C) + D as follows
P = 2 Pi / | B |
Hence we need to reduce the power of the given function using the identity sin2(x) = 1/2 - 1/2 cos(2x) as follows
f(x) = 3 sin 2(2x + Pi/4) = 3 [ 1/2 - 1/2 cos 2((2x + Pi/4)) ]
= -3/2 cos (4x + Pi/2) + 3/2
Hence the period P of f(x) is given by
P = 2 Pi / | 4 | = Pi / 2
Solution
Out of the 10 tv sets, 3 are defective and therefore 7 are non defective. If you select 2 out of 10 tv and 1 is defective the second one is non defective. There are C(3,1) ways of selecting 1 defective out of 3 , C(7,1) ways of selecting 1 non defective out of 7 and C(10,2) ways of selecting 2 tv sets out of 10. Hence the probability P is given by
P = C(3,1)*C(7,1) / C(10,2) where C(n,r) is the combination of n terms taken r at the time.
= 7/15
Solution
We first find the size of the third angle C
C = 180o - (50o + 32o) = 98o
We now use the sine law to find the length of side AB
AB / sin(C) = BC / sin(A)
Solve the above for AB, substitute and evaluate
AB = sin(C) * BC / sin(A) = sin(98) * 150 / sin(32) = 280 (rounded to the nearest unit)
Solution
Let P(x) = x3 - 2x2 + 3kx + 18. Using the remainder theorem, the remainder R of the division of P(x) by x - 6 is equal to P(6). Hence
R = P(6) = 63 - 2(6)2 + 3(6) k + 18
= 216 - 72 + 18 k + 18 = 162 + 18 k
Set R = 0 and solve for k
162 + 18 k = 0 , gives k = - 9
Solution
The rates RA and RA of pumps A and B are given by
RA = 1/4 and RB = 1/6
Let t be the time that the two pumps will take to empty 50% of the pool. Hence
t(1/4 + 1/6) = 0.5
Multiply all terms in the above equation by the lcm of 4 and 6 which 12, simplify and solve
t(3 + 2) = 6 t = 6/5 = 1.2 hours = 1 hour 12 minutes
A) a circle
B) an ellipse
C) a horizontal line
D) a hyperbola
E) a vertical line
Solution
If r and Θ are the polar coordinates then the x and y coordinates are given by
x = r cos(Θ) and y = r sin(Θ) and x2 + y2 = r2cos2(Θ) + r2sin2(Θ) = r2
Multiply both sides of the given equation r = 10 cos(Θ) by r
r2 = 10 r cos(Θ)
Substitute r2 by x2 + y2 and r cos(Θ) by x in the above equation to obtain
x2 + y2 = 10 x
The above equation may be written as
x2 - 10 x + y2 = 0
(x - 5)2 + y2 = 25
The above equation is that of a circle of center (5,0) and radius 5. Hence the given equation r = 10 cos(Θ) is that of a circle.
Solution
We first expand the left side of the given equation.
2 a - 2b i - i a - b = 2 + 9 i
which may be written as
2 a - b + i(-2 b - a) = 2 + 9 i
Two complex numbers are equal if their real parts and imaginary are equal. Hence the above equation gives two other equations
2 a - b = 2 and - 2 b - a = 9
Solve the above system of equation to find a = - 1.
A) (0 , 3)
B) (1 , 1)
C) (3 , 1)
D) (5 , 0)
E) (6 , 7)
Solution
We first find the slope m1 of line L1 since we know two points on this line.
m1 = (2 - 3) / (0 - 2) = 1 / 2
Since L1 and L2 are perpendicular, the slope m2 of line L2 is related to m1 as follows
m1*m2 = -1 or (1/2) * m2 = -1 which gives m2 = -2
We now know a point and a slope of line L2, hence its equation is given by
y - 3 = -2 (x - 2)
We now substitute the coordinates in the equation above and determine which point is on the line L2. Point (3 , 1) in C) is on L2.
 .
.
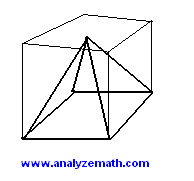
The cube has 6 square faces. The total surface is 24 square cm and therefore the area of one square face of the cube is
24 / 6 = 4 square cm and the side of one square face is 2 cm
The volume of the pyramid is equal to the one third the area of the base which is 4 square cm times the height. Since the pyramid is inscribed in the cube, the height is equal to a side of the square.
Volume = (1/3) * 4 * 2 = 8/3 cubic cm
x = cos2t
y = 3 sint -1
is
Solution
Let us solve the given equation y = 3 sint -1 for sin t
sin t = (y + 1) / 3
Square both sides of the above equation
sin2t = (y + 1)2 / 9
The above equation may be written
1 - cos2t = (y + 1)2 / 9
We now substitute cos2t by x in the above equation to obtain
1 - x = (y + 1)2 / 9
Solve the above for x
x = - (y + 1)2 / 9 + 1
The above equation is that of a parabola with axis parallel to x axis. However there are restrictions on both x and y. Since x = cos2t and y = 3 sint -1, x cannot be greater than 1 for example. So the graph defined by the parabolic equations is not a whole parabola but a part of a parabola.
 .
.
Solution
Calculating the limit as is gives an undetermined form 0 / 0 . Rewrite the numerator in factored form and simplify
(x4 - 16) / (x - 2) = (x2 - 4)(x2 + 4) / (x - 2)
= (x - 2)(x + 2)(x2 + 4) / (x - 2)
= (x + 2)(x2 + 4) , after simplification
The limit as x approaches 2 is given by
(2 + 2)(22 + 4) = 32
Solution
Use the change of base formula and log with base to rewrite log16(x) as follows
log16(x) = log2(x) / log2(16)
= log2(x) / log2(24)
= log2(x) / 4
= 0.25 log2(x)
 .
.
Solution
We first find the limit of f(x) as x approaches 0.
f(x) = (2x 2 + 5x) / x = 2x + 5
The limit of the above as x approaches 0 is.
2(0) + 5 = 5
For a function to be continuous at x = 0, the following condition must be satisfied
lim f(x) as x approaches = f(0)
5 = 3k - 1
Solve the above for k.
k = 2
Solution
We first divide all terms in the equation by 2 to obtain
2x + 3y = 4
We next substitute x by logb(a) and y by logb(c) in the above equation.
2 logb(a) + 3 logb(c) = 4
We next use the power formula to rewrite the above as .
logb(a2) + logb(c3) = 4
Using the product formula, the above is rewritten as
logb(a2 . c3) = 4
Solution
The x coordinate of the given point is the only coordinate equal to 0 and therefore the given point is on the yz plane
Solution
Let us square both sides of the given equation to obtain
y 2 = 9 - x 2
Rewrite as the equation of a circle in standard form.
x 2 + y 2 = 9
The above equation is that of a circle with radius 3 and center at (0,0). The region bounded by curve C, the x axis and the y axis and such that x≥ 0 is a quarter of this circle and therefore its area is the quarter of the area of the circle and is given by
(1/4) Pi (3 2) = 9 Pi / 4
Solution
A triangle is defined by any 3 non collinear points. Hence the number of triangles that 6 points can determine is equal to the number of combinations of 6 points taken 3 at the time and is given by
C(6,3) = 6! / (3!(6-3)!) = 6*5*4*3! / (3!3!) = 20
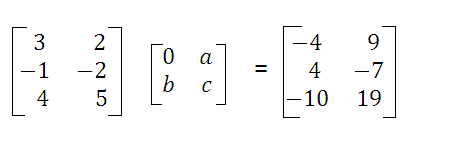 .
.
Solution
What is given is the multiplication of two matrices A.B = c. The product of the first row of A by the the first column of B gives
3(0) + 2(b) = - 4
Solve for b
b = - 2
The product of the first row of A by the the second column of B gives
3 a + 2 c = 9
The product of the second row of A by the the second column of B gives
- a - 2 c = - 7
Solve the last two equations for a and c simultaneously to obtain
a = 1 and c = 3
Solution
We first write 0.353535...as a sum as follows
0.353535... = 0.35 + 0.0035 + 0.000035 ....
The above is an infinite geometric series with common ration 0.001. Hence the sum
= 0.35 / (1 - 0.01) = 0.35 / 0.99 = 35 / 99
We proceed in the same way for 0.252525...
0.252525... = 0.25 + 0.0025 + 0.000025 +....
= 0.25 / (1 - 0.01) = 25 / 99
The sum is given by
0.353535... + 0.252525... = 35/99 + 25/99 = 60/99 = 20/33
The product of numerator and denominator
20 * 33 = 660
Solution
Define arc t as follows
t = tan-1√2
tan t = opposite side / adjacent side = √2 = √2 / 1
Hypotenuse = √(1 + 2) = √3
sin(tan-1√2) = sin t
= opposite side / hypotenuse = √2 / √3 = 0.82 (approximated at two decimal places)
Solution
Equation 8x = 2 may be written as follows
(23)x = 2
Hence
3x = 1 or x = 1/3
Equation 3x+y = 81 may be written as follows
3x+y = 81 = 34
Hence
x + y = 4 , y = 4 - x = 4 - 1/3 = 11/3
Solution
Let us first find the equation for g(x).
When - x2 / 2 is translated 2 units up it becomes - x2 / 2 + 2.
g(x) = - (x + 3)2 / 2 + 2 , translated 3 units left
g(1/2) = - (1/2 + 3)2 / 2 + 2 = - 33/8