What is Conditional Probability?
Conditional probability measures the probability of event A occurring given that event B has already occurred. We denote this as \( P(A|B) \) and calculate it using:
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \quad \text{for} \quad P(B) \neq 0 \]Where \( P(A \cap B) \) is the probability of both events occurring together.
Understanding Conditional Probability
Example 1: Basic Concept with Die Roll
- What is the probability that a fair die shows 1, 2, or 3?
- Given that the number rolled is odd, what is the probability it's 1, 2, or 3?
Solution
Part (a):
Sample space: \( S = \{1,2,3,4,5,6\} \), \( n(S) = 6 \)
Event A (rolling 1, 2, or 3): \( A = \{1,2,3\} \), \( n(A) = 3 \)
Using classical probability:
\[ P(A) = \frac{n(A)}{n(S)} = \frac{3}{6} = \frac{1}{2} \]
Part (b):
Event B (odd number): \( B = \{1,3,5\} \)
The Venn diagram shows the relationship:
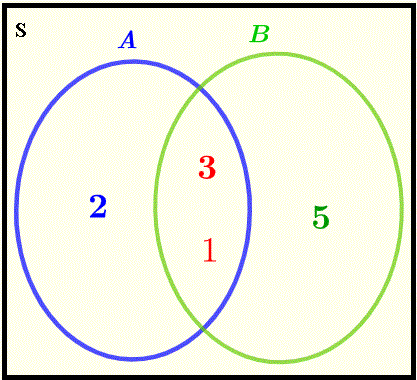
Given B occurred, we restrict to B's sample space. The intersection \( A \cap B = \{1,3\} \) has 2 elements:
\[ P(A|B) = \frac{n(A \cap B)}{n(B)} = \frac{2}{3} \]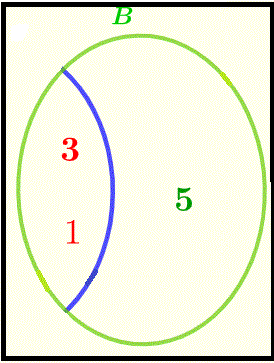
Dividing numerator and denominator by \( n(S) \) gives the general formula: \[ P(A|B) = \frac{ \frac{n(A \cap B)}{n(S)} }{ \frac{n(B)}{n(S)} } = \frac{P(A \cap B)}{P(B)} \]
Formal Definition
The conditional probability of A given B is: \[ P(A|B) = \frac{P(A \cap B)}{P(B)} \] valid when \( P(B) \neq 0 \).
Detailed Examples with Solutions
Example 2: Fruit Preferences
In a group of kids, the probability a randomly selected child likes oranges is 0.6. The probability they like both oranges and apples is 0.3. If a child who likes oranges is selected, what's the probability they also like apples?
Solution
Let O = likes oranges, A = likes apples
Given: \( P(O) = 0.6 \), \( P(A \cap O) = 0.3 \)
Using conditional probability formula:
\[ P(A|O) = \frac{P(A \cap O)}{P(O)} = \frac{0.3}{0.6} = 0.5 \]
So there's a 50% chance an orange-liker also likes apples.
Example 3: Electronics Purchase Survey
Survey of 100 people who bought mobile phones or tablets:
| Mobile Phone | Tablet | Total | |
|---|---|---|---|
| Brand A | 20 | 10 | 30 |
| Brand B | 30 | 40 | 70 |
| Total | 50 | 50 | 100 |
Random selection from the group. Find:
- Probability bought brand B
- Probability bought a mobile phone from brand B
- Probability bought a mobile phone given they bought brand B
Solution
Let Mp = bought mobile phone, T = bought tablet, A = brand A, B = brand B
- \( P(B) = \frac{70}{100} = 0.7 \)
- \( P(Mp \cap B) = \frac{30}{100} = 0.3 \)
- Using formula: \( P(Mp|B) = \frac{P(Mp \cap B)}{P(B)} = \frac{0.3}{0.7} = \frac{3}{7} \)
Alternative method (restricted sample space): Among 70 brand B buyers, 30 bought mobiles: \[ P(Mp|B) = \frac{30}{70} = \frac{3}{7} \]
Example 4: Card Deck Probabilities

Single card drawn from 52-card deck. Find:
- Probability of a King
- Probability of a red card
- Probability of a King that's red
- Probability of a King given it's red
- Probability it's red given it's a King
- Probability it's a Queen given it's a Heart
Solution
- \( P(\text{King}) = \frac{4}{52} = \frac{1}{13} \)
- \( P(\text{red}) = \frac{26}{52} = \frac{1}{2} \)
- \( P(\text{King} \cap \text{red}) = \frac{2}{52} = \frac{1}{26} \)
- Formula: \( P(\text{King}|\text{red}) = \frac{P(\text{King} \cap \text{red})}{P(\text{red})} = \frac{1/26}{1/2} = \frac{1}{13} \)
Restricted space: Among 26 red cards, 2 are Kings: \( \frac{2}{26} = \frac{1}{13} \) - Formula: \( P(\text{red}|\text{King}) = \frac{P(\text{red} \cap \text{King})}{P(\text{King})} = \frac{1/26}{1/13} = \frac{1}{2} \)
Restricted space: Among 4 Kings, 2 are red: \( \frac{2}{4} = \frac{1}{2} \) - Formula: \( P(\text{Queen}|\text{Heart}) = \frac{P(\text{Queen} \cap \text{Heart})}{P(\text{Heart})} = \frac{1/52}{13/52} = \frac{1}{13} \)
Restricted space: Among 13 Hearts, 1 is Queen: \( \frac{1}{13} \)
Example 5: Car Dealership Inventory
Car inventory by type and color:
| SUV | Sport Car | Van | Coupe | Total | |
|---|---|---|---|---|---|
| Black | 35 | 10 | 25 | 15 | 85 |
| White | 10 | 15 | 20 | 5 | 50 |
| Blue | 15 | 15 | 5 | 30 | 65 |
| Total | 60 | 40 | 50 | 50 | 200 |
Random car selection. Find:
- Probability it's black given it's a Van
- Probability it's an SUV given it's white
- Probability it's blue given it's a Coupe
Solution
Total cars: 200
- Formula: \( P(\text{black}|\text{Van}) = \frac{P(\text{black} \cap \text{Van})}{P(\text{Van})} = \frac{25/200}{50/200} = \frac{1}{2} \)
Restricted: Among 50 Vans, 25 black: \( \frac{25}{50} = \frac{1}{2} \) - Formula: \( P(\text{SUV}|\text{white}) = \frac{P(\text{SUV} \cap \text{white})}{P(\text{white})} = \frac{10/200}{50/200} = \frac{1}{5} \)
Restricted: Among 50 white cars, 10 SUVs: \( \frac{10}{50} = \frac{1}{5} \) - Formula: \( P(\text{blue}|\text{Coupe}) = \frac{P(\text{blue} \cap \text{Coupe})}{P(\text{Coupe})} = \frac{30/200}{50/200} = \frac{3}{5} \)
Restricted: Among 50 Coupes, 30 blue: \( \frac{30}{50} = \frac{3}{5} \)
Example 6: Insurance Survey
Survey of 100 people: 40% have both home and car insurance with the company. Probability of car insurance is 0.7. What's the probability of home insurance given car insurance?
Solution
Let H = home insurance, C = car insurance
Given: \( P(C) = 0.7 \), \( P(H \cap C) = 0.4 \)
Using conditional probability:
\[ P(H|C) = \frac{P(H \cap C)}{P(C)} = \frac{0.4}{0.7} = \frac{4}{7} \approx 0.571 \]
So 57.1% of car insurance holders also have home insurance.
Example 7: Sports Participation Survey
200 students surveyed: 120 play football, 50 play basketball, 20 play both.
- Probability a student plays football given they play basketball?
- Probability a student plays basketball given they play football?
- Probability a student plays football given they play exactly one sport?
Solution
Let F = plays football, B = plays basketball
Probabilities: \( P(F) = 120/200 = 0.6 \), \( P(B) = 50/200 = 0.25 \), \( P(F \cap B) = 20/200 = 0.1 \)
- \( P(F|B) = \frac{P(F \cap B)}{P(B)} = \frac{0.1}{0.25} = 0.4 \)
- \( P(B|F) = \frac{P(B \cap F)}{P(F)} = \frac{0.1}{0.6} \approx 0.167 \)
- Let O = plays exactly one sport
Students playing exactly one sport: \( (120-20) + (50-20) = 130 \)
\( P(O) = 130/200 = 0.65 \)
Students playing football and exactly one sport: \( 120-20 = 100 \)
\( P(F \cap O) = 100/200 = 0.5 \)
\( P(F|O) = \frac{P(F \cap O)}{P(O)} = \frac{0.5}{0.65} \approx 0.769 \)


Practice Problems
Question 1
A die is rolled. Find the probability of an even number given the number is greater than 3.
Question 2
A card is drawn from a 52-card deck. Find the probability of getting a 3 given the card is red.
Question 3
120 people surveyed: 90 own cars, 40 own bicycles, 10 own neither. Random selection:
- Probability owns both car and bicycle?
- Probability owns car given they own bicycle?
- Probability owns bicycle given they own car or bicycle but not both?
Question 4
Company A: 70 products (40 software, 30 hardware). Company B: 50 products (x hardware, y software).
- Probability product is hardware given it's from Company B? (in terms of y)
- Probability product is hardware given it's from Company A?
- For what y values is probability in (a) greater than in (b)?
Question 5
Financial analyst: P(stock market down | economy deteriorates) = 0.8. P(economy deteriorates) = 0.5. What's P(economy deteriorates and stock market down)?
Detailed Solutions
Solution to Question 1
Sample space: \( S = \{1,2,3,4,5,6\} \)
Event E (even): \( E = \{2,4,6\} \)
Event G (>3): \( G = \{4,5,6\} \)
Intersection: \( E \cap G = \{4,6\} \)
Using formula:
\[ P(E|G) = \frac{P(E \cap G)}{P(G)} = \frac{2/6}{3/6} = \frac{2}{3} \]
Restricted sample space: Among numbers >3 (4,5,6), two are even (4,6): \( \frac{2}{3} \)
Solution to Question 2
Event T (getting 3): \( P(T) = 4/52 = 1/13 \)
Event R (red card): \( P(R) = 26/52 = 1/2 \)
Intersection: \( P(T \cap R) = 2/52 = 1/26 \)
Using formula:
\[ P(T|R) = \frac{P(T \cap R)}{P(R)} = \frac{1/26}{1/2} = \frac{1}{13} \]
Restricted sample space: Among 26 red cards, 2 are 3's: \( \frac{2}{26} = \frac{1}{13} \)
Solution to Question 3
Let C = owns car, B = owns bicycle
Let x = number owning both. From total: \( (90-x) + (40-x) + x + 10 = 120 \)
Solving: \( 140 - x = 120 \) ⇒ \( x = 20 \)
- \( P(C \cap B) = 20/120 = 1/6 \)
- \( P(C|B) = \frac{P(C \cap B)}{P(B)} = \frac{1/6}{40/120} = \frac{1/6}{1/3} = \frac{1}{2} \)
- Let COB = car or bicycle but not both
Number in COB: \( (90-20) + (40-20) = 70 + 20 = 90 \)
\( P(COB) = 90/120 = 3/4 \)
\( P(B \cap COB) = 20/120 = 1/6 \) (those with bicycles only)
\( P(B|COB) = \frac{P(B \cap COB)}{P(COB)} = \frac{1/6}{3/4} = \frac{2}{9} \)
Solution to Question 4
Total products: \( 70 + 50 = 120 \)
For Company B: \( x + y = 50 \)
Let H = hardware product, A = from Company A, B = from Company B
- \( P(H|B) = \frac{P(H \cap B)}{P(B)} = \frac{y/120}{50/120} = \frac{y}{50} \)
- \( P(H|A) = \frac{P(H \cap A)}{P(A)} = \frac{30/120}{70/120} = \frac{30}{70} = \frac{3}{7} \)
- Need \( \frac{y}{50} > \frac{3}{7} \)
Multiply: \( 7y > 150 \)
\( y > \frac{150}{7} \approx 21.43 \)
Since y is integer: \( y \geq 22 \)
Solution to Question 5
Let E = economy deteriorates, S = stock market down
Given: \( P(S|E) = 0.8 \), \( P(E) = 0.5 \)
Using conditional probability definition:
\[ P(S|E) = \frac{P(S \cap E)}{P(E)} \]
Rearranging:
\[ P(S \cap E) = P(S|E) \times P(E) = 0.8 \times 0.5 = 0.4 \]
So probability both occur is 0.4 or 40%.