Law of Total Probability Examples

The law of total probability is explained and used to solve examples including detailed explanations.

Explanation of the Law of Total Probability

Let the sample space \( S \) be partioned into \( n \) mutually exclusive events \( E_1 \), \( E_2\), \( E_3\) ... \( E_n \) and collectively exhaustive (covering the entire sample space \( S \) ).


Note that
\( A = (A \cap E_1) \cup (A \cap E_2) \cup (A \cap E_3) ... \cup (A \cap E_n) \)
and since the events \( E_i \) are all mutually exclusive, then \( (A \cap E_i) \) are also all mutually exclusive and therefore we can use the addition rule of probabilities to write
\[ P(A) = P(A \cap E_1) + P(A \cap E_2) + P(A \cap E_3) ... P(A \cap E_n) \]
Using the definition of conditional probabilities we write
\( P(A \cap E_n) = P(A | E_n) P(E_n) \),
and rewrite the law of total probability as
\[ P(A) = P(A | E_1) P(E_1) + P(A | E_2) P(E_2) + P(A | E_3) P(E_3) ... P(A | E_n) P(E_n) \] \[ = \sum_{i=1}^{n} P(A | E_i) P(E_i) \] Note that because \( E_1 \), \( E_2\), \( E_3\) ... \( E_n \) are collectively exhaustive, we have
\( \sum_{i=1}^{n} P(E_i) = 1 \)

The Law of Total Probability Examples with Detailed Solutions

Example 1
We have three similar bags B1, B2 and B3 containing 4 balls each. B1 contains 2 red and 2 blue balls, B2 contains 3 red and 1 blue balls and B3 contains 1 red and 3 blue balls. One bag is selected at random and a ball is selected at random from that bag.
What is the probability that the ball is red?

Solution to Example 1
We start by a diagram that explains what is given.


We present T two methods to solve the above question:
Method 1: Use classical method of calculating probabilities
In all three bags there is a total of 12 balls 6 of which are red balls. Let event \( A \) be that of selecting a red ball. Hence the probability that the ball selected is red is given by
\( P(A) = 6/12 = 1/2 \)
Method 2: Use law of total probability
Let \( E_1 \), \( E_2 \) and \( E_3 \) be the event of selectiong bag \( B_1 \), \( B_2 \) and \( B_3 \) respectively and \( A \) be the event of selecting a red ball.
\( P(A) = P(A | E_1) P(E_1) + P(A | E_2) P(E_2) + P(A | E_3) P(E_3)\)
The bags are similar and are therefore equally likely to be selected. The probabilities of selecting bags \( B_1 \), \( B_2 \) or \( B_3 \) at random are given by
\( P(E_1) = 1/3 \) (one bag B1 out of 3 bags)
\( P(E_2) = 1/3 \) (one bag B2 out of 3 bags)
\( P(E_3) = 1/3 \) (one bag B3 out of 3 bags)
The conditional probabilities of selecting a red ball given that it is in bag \( B_1\), \( B_2 \) and \( B_3 \) are given by
\( P(A | E_1) = 2/4 = 1/2 \) (2 red balls out of a total of 4 balls in B1)
\( P(A | E_2) = 3/4 \) (3 red balls out of a total of 4 balls in B2)
\( P(A | E_3) = 1/4 \) (1 red ball out of a total of 4 balls in B3)
We now use the law of total probability
\( P(A) = (1/2)(1/3) + (3/4)(1/3) + (1/4)(1/3) = 1/2 \)

Example 2
Students in a math class where 40% are males and 60% are females took a test. 50% of the males and 70% of the females passed the test. What percent of students passed the test?

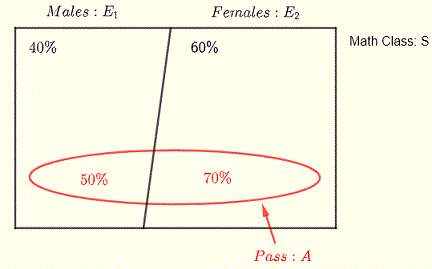
Solution to Example 2
We start by drawing a diagram with the whole class including the males and females groups.
Let events \( E_1 \) "be a male" and \( E_2 \) "be a female", and event \( A \) "passed the test".

The law of total probability gives
\( P(A) = P(A | E_1) P(E_1) + P(A | E_2) P(E_2) \)
\( = 50\% \times 40\% + 70\% \times 60\% = 62\% \)

Example 3
Three factories produce the same tool and supply it to the market. Factory A produces 30% of the tools for the market and the remaining 70% of the tools are produced in factories B and C. 98% of the tools produced in factory A, 95% of the tools produced in factory B and 97% of the tools produced in factory C are not defective.
What percent of tools should be produced by factories B and C so that a tool picked at random in the market will have a probability of being non defective equal to 96%?

Solution to Example 3
We start by drawing a diagram of all three factories.
Let \( A \), \(B\) and \( C \) be the events of tools produced by factories A, B and C and \( ND \) be the event "non defective".
\( x \) and \( y \) are the percentages of tools to be produced by companies B and C respectively.

Using the above diagram, we can write
\( P(A) = 30\% \) , \( P(B) = x \) , \( P(C) = y \)
The three factories supply the whole market; hence
\( 30\% + x + y = 100\% \) which gives \( y = 70\% - x \)
Use the law of total probability to write the equation
\( P(ND) = P(ND|A) P(A) + P(ND|B) P(B) + P(ND|C) P(C) \)
\( = 98\% \times 30\% + 95\% \times x + 97\% \times (70\% - x) = 96\% \)
Solve for \( x \)
Company B produces: \( x = 0.65 = 65\% \)
Company C produces: \( y =70\% - 65\% = 5\%\)

Example 4
5% of a population have a flu and the remaining 95% do not have this flu.
A test is used to detect the flu and this test is positive in 95% of people with a flu and is also (falsely) positive in 1% of the people with no flu.
If a person from this population is randomly selected and tested, what is the probability that the test is positive?

Solution to Example 4
Use the total probability theorem to find the percentage as follows:
\( 5\% \times 95\% + 95\% \times 1\% = 5.7\% \)

More References and links