Relations in Mathematics

The definition of a relation in mathematics, along with its domain and range, is presented with examples, questions and their solutions.

Definition of a Relation in Mathematics

A relation is a correspondence between two sets called the domain and the range [1].

Example 1

The relation \( R_1 \) between a group of four students \( \{ \; \text{Sasha}\; , \; \text{Smith} \; , \; \text{Jane} \; , \; \text{John} \; \} \) and their exam scores \( \{ \; 85 \; , \; 92 \; , \; 71 \; \} \) is shown in the diagram below.

Relation between students and their exam scores — Fig.1 - Relation \( R_1 \) Between Students and Their Scores

The above relation \( R_1 \) may be represented as a set of ordered pairs:

\( R_1 = \{ \; (\text{Sasha} \; , \; 85) \; , \; (\text{Smith} \; , \; 85) \; , \; (\text{Jane} \; , \; 92) \; , \; (\text{John} \; , \; 71) \; \} \)

The first element in each ordered pair is an element of the domain and the second element is the corresponding element of the range.

The domain \( D \) of the relation \( R_1 \): \( D = \{ \; \text{Sasha}\; , \; \text{Smith} \; , \; \text{Jane} \; , \; \text{John} \; \} \)

The range \( R \) of the relation \( R_1 \): \( R = \{ \; 85 \; , \; 92 \; , \; 71 \; \} \)

Example 2

The relation \( R_2 \) between match times \( \{ 10 \; \text{am} \; , \; 1 \; \text{pm} \; , \; 4 \; \text{pm} \} \) and team pairs \( \{ \text{A vs B} \; , \; \text{C vs D} \; , \; \text{E vs F} \; , \; \text{G vs H} \} \) is shown below.

Relation between time and matches — Fig.2 - Relation \( R_2 \) Time and Matches

The relation \( R_2 \) as ordered pairs:

\( R_2 = \{ \; (10 \; \text{am} \; , \; \text{A vs B}) \; , \; (1 \; \text{pm} \; , \; \text{C vs D}) \; , \; (4 \; \text{pm} \; , \; \text{E vs F}) \; , \; (4 \; \text{pm} \; , \; \text{G vs H}) \; \} \)

The domain \( D \): \( D = \{ \; 10 \; \text{am} \; , \; 1 \; \text{pm} \; , \; 4 \; \text{pm} \; \} \)

The range \( R \): \( R = \{ \; \text{A vs B} \; , \; \text{C vs D} \; , \; \text{E vs F} \; , \; \text{G vs H} \; \} \)

Representations of Relations

Different methods to represent mathematical relations:

Relations Represented by Venn Diagrams

Relations use sets for domain and range with arrows connecting corresponding elements.

Relation represented by Venn diagrams — Fig.3 - Relation Represented by Venn Diagrams

Relations Represented as Ordered Pairs

A relation represented as a set of ordered pairs:

\( R_3 = \{ \; (2,3) \; , \; (4,1) \; , \; (6,4) \; , \; (7,2) \; , \; (7,6) \; \} \)

Relations Represented by Tables

A table with domain values in one row and corresponding range values in another:

\( x \)	\( 2 \)	\( 4 \)	\( 6 \)	\( 7 \)	\( 7 \)
\( y \)	\( 3 \)	\( 1 \)	\( 4 \)	\( 2 \)	\( 6 \)

Relations Represented by Graphs

Rectangular coordinate system with points representing ordered pairs \((x,y)\).

Relation represented by graphs — Fig.4 - Relation Represented by a Graph

Relations Represented by Equations

The equation \( y = 3x + 1 \) defines a relation between \( x \) and \( y \). For given \( x \) values:

\( x \)	\( -3 \)	\( 0 \)	\( 5 \)	\( 8 \)
\( y \)	\( -8 \)	\( 1 \)	\( 16 \)	\( 25 \)

Example 3

Given relation \( R_4 = \{ \; (-1,3) \; , \; (2,4) \; , \; (5,7) \; , \; (2,6) \; \} \):

a) Find domain and range
b) Represent as graph
c) Represent as table
d) Represent as Venn diagram

Solution

a) Domain \( D = \{ -1, 2, 5 \} \), Range \( R = \{ 3, 4, 6, 7 \} \)

b) Graph representation:

Graph for Example 3 — Fig.5 - Relation \( R_4 \) Graph Representation

c) Table representation:

\( x \)	\( -1 \)	\( 2 \)	\( 2 \)	\( 5 \)
\( y \)	\( 3 \)	\( 4 \)	\( 6 \)	\( 7 \)

d) Venn diagram representation:

Venn diagram for Example 3 — Fig.6 - Relation \( R_4 \) Venn Diagram

Practice Questions

Part A

Relation \( R_5 \) is given by its graph:

a) Represent as ordered pairs, table, and Venn diagram
b) Find domain and range

Part B

Relation \( R_6 \) is given by table:

\( x \)	\( -2 \)	\( -2 \)	\( -2 \)	\( 0 \)	\( 1 \)	\( 3 \)
\( y \)	\( 3 \)	\( 4 \)	\( 5 \)	\( 4 \)	\( 0 \)	\( 0 \)

a) Find domain and range
b) Represent as ordered pairs and Venn diagram

Part C

a) Give two different relations with same domain
b) Give two different relations with same range
c) Give two different relations with same domain and range

Part D

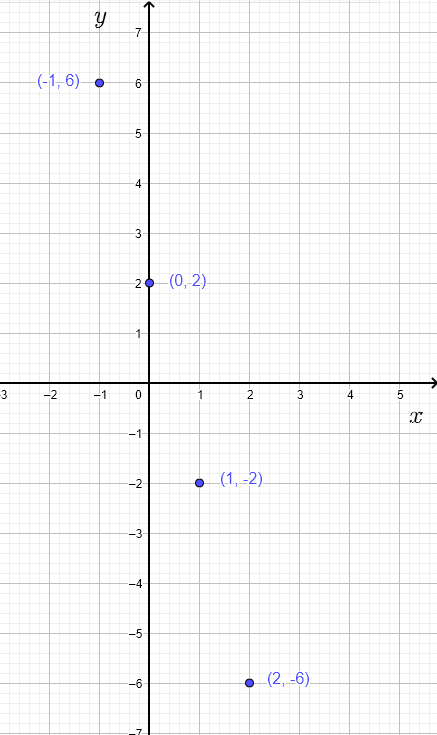
Relation defined by \( y + 4x = 2 \) with \( x \in \{ -1, 0, 1, 2 \} \):
a) Use table to find corresponding \( y \) values
b) Represent graphically

Solutions

Part A Solutions

a) \( R_5 = \{ (-2,2), (1,1), (2,1), (2,5), (4,2), (4,3), (4,4) \} \)

Table representation:

\( x \)	-2	1	2	2	4	4	4
\( y \)	2	1	1	5	2	3	4

Venn diagram:

b) Domain \( D = \{ -2, 1, 2, 4 \} \), Range \( R = \{ 1, 2, 3, 4, 5 \} \)

Part B Solutions

a) Domain \( D = \{ -2, 0, 1, 3 \} \), Range \( R = \{ 0, 3, 4, 5 \} \)

b) \( R_6 = \{ (-2,3), (-2,4), (-2,5), (0,4), (1,0), (3,0) \} \)

Venn diagram solution Part B — Fig.9 - Relation \( R_6 \) Venn Diagram Solution

Part C Solutions

a) \( \{ (-3,3), (-2,4), (0,5), (4,5) \} \) and \( \{ (-3,3), (-2,8), (0,5), (4,0) \} \)

b) \( \{ (0,3), (-2,5), (6,5), (7,5) \} \) and \( \{ (-3,3), (-2,5), (0,5), (9,5) \} \)

c) \( \{ (-1,0), (0,-5), (4,5), (7,8) \} \) and \( \{ (-1,0), (-1,-5), (0,-5), (4,5), (7,8) \} \)

Part D Solutions

a) Table of values:

\( x \)	-1	0	1	2
\( y \)	6	2	-2	-6

b) Graph:

Graph solution Part D — Fig.10 - Relation \( y + 4x = 2 \) Graph Solution

References and Further Reading

[1] Algebra and Trigonometry - R.E. Larson, R.P. Hostetler, B.H. Edwards, D.E. Heyd - 1997 - ISBN: 0-669-41723-8

Additional Resources: