Math Problems with Solutions for Grade 10
Challenging and engaging Grade 10 math word problems with detailed solutions and answers. Topics include quadratic functions, systems of equations, exponents, equations of circles, rational expressions, geometry, triangles, trigonometry, speed problems, and more.
Question 1
A ball is thrown upward from the top of a 20-meter-high building. Its height \( h \) in meters after \( t \) seconds is given by: \[ h(t) = -5t^2 + 15t + 20 \] a) How long does it take for the ball to reach its maximum height?
b) What is the maximum height the ball reaches?
c) When does the ball hit the ground?
a) Maximum height occurs at the vertex of the parabola: \[ t = \frac{-b}{2a} = \frac{-15}{2(-5)} = \frac{15}{10} = 1.5\ \text{seconds} \] b) Substitute \( t = 1.5 \) into the equation to obtain the maximum height: \[ h(1.5) = -5(1.5)^2 + 15(1.5) + 20 = -11.25 + 22.5 + 20 = 31.25\ \text{meters} \] c) Set \( h(t) = 0 \): \[ -5t^2 + 15t + 20 = 0 \Rightarrow t^2 - 3t - 4 = 0 \] Factor: \[ (t - 4)(t + 1) = 0 \Rightarrow t = 4\ \text{or}\ t = -1 \] Time cannot be negative, hence the ball hits the ground \( 4 \) seconds after it was thrown.
Question 2
You have \( 30 \) coins in dimes and quarters. Their total value is \( \$5.10 \).
a) Set up a system of equations to represent the situation.
b) Solve the system to find how many dimes and quarters you have.
a) Let:
\( d \): number of dimes and \( q \): number of quarters
Total number of coins is \(30\) \[ d + q = 30 \quad \text{(1)} \] A dime is worth \( 10 \) cents and a quarter is worth \( 25 \) cents, hence \[ 0.10d + 0.25q = 5.10 \quad \text{(2)} \] b) From equation (1): \( d = 30 - q \)
Substitute into equation (2): \[ 0.10(30 - q) + 0.25q = 5.10 \] Expand and simplify \[ 3 - 0.10q + 0.25q = 5.10 \] \[ 0.15q = 2.10 \] \[ q = 14 \] Then \( d = 16 \)
You have \( 16 \) dimes and \( 14 \) quarters.
Question 3
A circle has a center at \( (3,-2) \) and passes through the point \( (6,2) \).
a) Find the radius of the circle.
b) Write the equation of the circle in standard form: \[ (x-a)^2+(y-b)^2=r^2 \] where \( (a,b) \) is the center of the circle.
a) The radius is distance from the center to any point on the circle, hence the use of the distance formula to find the radius \( r \) using the center \( (3,-2) \) and the point \( (6,2) \): \[ r = \sqrt{(6 - 3)^2 + (2 - (-2))^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \] b) The Equation of the circle is given by: \[ (x - 3)^2 + (y + 2)^2 = 25 \]
Question 4
Simplify: \[ \frac{x^2 - 9}{x^2 - x - 6} \cdot \frac{x - 2}{x + 3} \]
Factor all expressions** \[ x^2 - 9 = (x - 3)(x + 3)\] \[ x^2 - x - 6 = (x - 3)(x + 2) \] Now substitute in the given expression: \[ \frac{(x - 3)(x + 3)}{(x - 3)(x + 2)} \cdot \frac{x - 2}{x + 3} \] Cancel common factors \( x - 3 \) and \( x + 3 \) to obtain: \[ \frac{x^2 - 9}{x^2 - x - 6} \cdot \frac{x - 2}{x + 3} = \frac{x - 2}{x + 2} \] When we cancel common factors, as was done above, we are dividing by common factors. We cannot divide by zero, therefore we need to impose the conditions that the common factors canceled cannot be zero: \[ x - 3 \ne 0 \Rightarrow x \ne 3 \] \[ x + 3 \ne 0 \Rightarrow x \ne - 3 \] The given expression simplies to: \[ \frac{x - 2}{x + 2}, \quad \text{where } x \ne -3,\ -3 \]
Question 5
Solve the equation: \[ \sqrt{2x + 3} = x - 1 \]
Square both sides: \[ (\sqrt{2x + 3})^2 = (x - 1)^2 \Rightarrow 2x + 3 = x^2 - 2x + 1 \] Rearrange: \[ 0 = x^2 - 4x - 2 \] Use quadratic formula: \[ x = \frac{4 \pm \sqrt{(-4)^2 - 4(1)(-2)}}{2(1)} = \frac{4 \pm \sqrt{16 + 8}}{2} \] \[ = \frac{4 \pm \sqrt{24}}{2} = \frac{4 \pm 2\sqrt{6}}{2} = 2 \pm \sqrt{6} \] Check for extraneous solutions:
Try \( x = 2 + \sqrt{6} \approx 4.45 \):
LHS (left hand side) = \( \sqrt{2(4.45) + 3} = \sqrt{11.9} \approx 3.45 \)
RHS (right hand side) = \( 4.45 - 1 = 3.45 \) ?
Try \( x = 2 - \sqrt{6} \approx -0.45 \):
LHS (left hand side) = \( \sqrt{2(-0.45) + 3} = \sqrt{-0.9 + 3} = \sqrt{2.1} \approx 1.45 \)
RHS (right hand side) = \( -0.45 - 1 = -1.45 \)
The solution \( x = 2 + \sqrt{6} \) verify both left and right sides of the given equation but \( x = 2 - \sqrt{6} \) does not and is therefore an extraneous solution.
The solution to the given equation is: \[ x = 2 + \sqrt{6} \]
Question 6
Given points: \( A(2, 3) \), \( B(6, 7) \), \( C(10, 5) \), \( D(6, 1) \) Prove that quadrilateral ABCD is a parallelogram .
Find slope of \( AB \) and \( CD \): \[ m_{AB} = \frac{7 - 3}{6 - 2} = \frac{4}{4} = 1 \] \[ m_{CD} = \frac{5 - 1}{10 - 6} = \frac{4}{4} = 1 \] Find slope of \( BC \) and \( AD \): \[ m_{BC} = \frac{5 - 7}{10 - 6} = \frac{-2}{4} = -0.5 \] \[ m_{AD} = \frac{1 - 3}{6 - 2} = \frac{-2}{4} = -0.5 \] Since both pairs of opposite sides are parallel, ABCD is a parallelogram.
Question 7
Solve for \( x \): \[ \dfrac{5^{2x}}{5} = 625 \]
First, express 625 as a power of 5: \[ 625 = 5^4 \] Use exponents rule to write \[ \dfrac{5^{2x}}{5} = 5^{2x-1} \] Rewrite the equation \[ 5^{2x - 1} = 5^4 \] which gives the algebraic equation \[ 2x - 1 = 4 \] Solve for \( x \) \[ x = \frac{5}{2} \]
Question 8
In triangle \( ABC \), side \( a = 7 \) cm, side \( b = 10 \) cm, and angle \( C = 120^\circ \). Find the length of side \( c \).
Use Cosine Law: \[ c^2 = a^2 + b^2 - 2ab\cos(C) \] \[ c^2 = 7^2 + 10^2 - 2(7)(10)\cos(120^\circ) \] \[ c^2 = 49 + 100 - 140(-0.5) \] \[ c^2 = 149 + 70 = 219 \] \[ c = \sqrt{219} \approx 14.8 \ \text{cm} \] Hence: \[ c \approx 14.8 \ \text{cm} \]
Question 9
The function \( f(x) = a(x - 2)^2 + 3 \) passes through the point \( (4, 15) \). What are the coordinates of the vertex?
Substitute \( x = 4 \), \( f(x) = 15 \) into the equation: \[ 15 = a(4 - 2)^2 + 3 \] Solve for \( a \) \[ 15 = a(2)^2 + 3 \] \[ a = 3 \] Function \( f(x) \) is a quadratic function given by: \[ f(x) = 3(x - 2)^2 + 3 \] From the form \( a(x - h)^2 + k \), the vertex is \[ (h, k) = (2, 3) \]
Question 11
From a point 50 m away, the angle of elevation to the top of a tower is \( 32^\circ \).
a) How tall is the tower?
b) If a drone is 30 m above the tower, what is the new angle of elevation from the same point to the drone?
a) Let \( h \) be the height of the tower. Use the tangent formula in a right triangle: \[ \tan(32^\circ) = \frac{\text{h}}{50} \] Solve for \( h \): \[ h = 50 \cdot \tan(32^\circ) \approx 50 \cdot 0.6249 = 31.2\ \text{m} \] b) Height of the drone: \[ 31.2 + 30 = 61.2 \] Let \( \theta) \) be the angle of elevation to the drone: \[ \tan(\theta) = \frac{61.2}{50} \] Hence \[ \theta = \tan^{-1}(1.224) \approx 50.2^\circ \]
Question 12
It takes a boat 3 hours to travel down a river from point A to point B, and 5 hours to travel up the river from B to A. How long would it take the same boat to go from A to B in still water (no current)?
Let:
\( S \) be the speed of the boat in still water (in km/h),
\( r \) be the speed of the river current (in km/h),
\( d \) be the distance between points A and B (in km).
From the given: Downstream: \[ d = 3(S + r) \] Upstream: \[ d = 5(S - r) \] Equating both expressions for \( d \): \[ 3(S + r) = 5(S - r) \] Expand both sides: \[ 3S + 3r = 5S - 5r \] Put terms with \( r \) one side and terms with \( s \) on the other side: \[ 8 r = 2 s \] Solve for \( r \) \[ r = \frac{S}{4} \] Now substitute \( r = \frac{S}{4} \) back into the equation for downstream: \[ d = 3\left(S + \frac{S}{4}\right) = 3\left(\frac{5S}{4}\right) = \frac{15S}{4} \] Now, in still water (no current), the speed is just \( S \). Time to travel from A to B in still water: \[ \text{Time} = \frac{d}{S} = \frac{\frac{15S}{4}}{S} = \frac{15}{4} = 3.75 \text{ hours} \] So, the time it would take the boat to go from A to B in still water is: \[ 3 \text{ hours and } 45 \text{ minutes} \]
Question 13
For what value of \( x \) will the function \[ f(x) = -3(x - 10)(x - 4) \] have a maximum value? Find the maximum value.
Expand the function: \[ f(x) = -3(x^2 - 14x + 40) = -3x^2 + 42x - 120 \] This is a quadratic function of the form: \[ f(x) = ax^2 + bx + c \quad \text{where } a = -3, \, b = 42 \] The function reaches its maximum at the vertex whose x coordinate is given by: \[ x = -\frac{b}{2a} = -\frac{42}{2(-3)} = \frac{42}{6} = 7 \] To find the maximum value, substitute \( x = 7 \) back into the function: \[ f(7) = -3(7 - 10)(7 - 4) = -3(-3)(3) = -3 \cdot -9 = 27 \] The function has a maximum at \( x = 7 \) and the maximum value of \( f(x) \) is \( f(7) = 27 \).
Question 14
A class has an average exam mark of \( 70 \). The average mark of students who scored below \( 60 \) is \( 50 \), and the average of students who scored \( 60 \) or more is \( 75 \). If the total number of students in the class is \( 20 \), how many students scored below \( 60 \)?
Let \( n \) be the number of students who scored below 60. and \( N \) be the number of students who scored 60 or more.
The average for students who scored below 60 is: \[ \frac{\sum X_i}{n} = 50 \Rightarrow \sum X_i = 50 n \] The average for students who scored 60 or more is: \[ \frac{\sum Y_i}{N} = 75 \Rightarrow \sum Y_i = 75 N \] The overall class average is 70: \[ \frac{\sum X_i + \sum Y_i}{20} = 70 \] Substitute: \[ \frac{50n + 75N}{20} = 70 \] Multiply all terms by \( 20 \) and simplify: \[ 50n + 75N = 1400 \quad (1) \] We also have: \[ n + N = 20 \Rightarrow N = 20 - n \] Substitute \( N \) into the equation (1): \[ 50n + 75(20 - n) = 1400 \] Expand and simplify: \[ -25n + 1500 = 1400 \] Solve for \( n \): \[ n = 4 \] \( n = 4 \) students who scored below 60.
Question 15
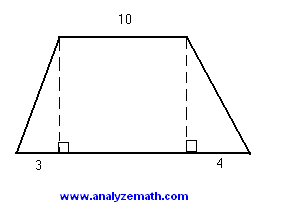
The area of the trapezoid is equal to 270 square units. Find its perimeter and round your answer to the nearest unit.
 .
.
Let \( h \) be the height of the trapezoid. \[ \text{Area} = \frac{1}{2} \cdot h (base_1 \; + \; base_2) = \frac{1}{2} \cdot h \cdot (10 + 10 + 3 + 4) = 270 \] Solve for \( h \): \[ h = 20 \] Apply the Pythagorean Theorem to the right triangle on the left (hypotenuse \( L \) ): \[ 20^2 + 3^2 = L^2 \quad \Rightarrow \quad L = \sqrt{409} \] Apply the Pythagorean Theorem to the right triangle on the right (hypotenuse \( R \) ): \[ 20^2 + 4^2 = R^2 \quad \Rightarrow \quad R = \sqrt{416} \] The perimeter of the trapezoid is: \[ \text{Perimeter} = \sqrt{409} + 10 + \sqrt{416} + 17 = 27 + \sqrt{409} + \sqrt{416} \; \text{units} \]
Question 16
The area of a rectangular field is equal to \( 300 \) square meters. Its perimeter is equal to \( 70 \) meters. Find the length and width of this rectangle.
Let the length be \( L \) meters and the width be \( W \) meters such that \( L \gt W \). Use the area to write: \[ L \times W = 300 \] Use the perimeter to write: \[ 2L + 2W = 70 \] Divide all terms of the equation \( \; 2L + 2W = 70 \; \) by 2: \[ L + W = 35 \] Solve for \( L \): \[ L = 35 - W \] Substitute into the area equation: \[ (35 - W) \cdot W = 300 \] Expand: \[ 35W - W^2 = 300 \] Rearrange into a standard quadratic form: \[ W^2 - 35W + 300 = 0 \] Solve using the quadratic formula: \[ W = \frac{35 \pm \sqrt{(-35)^2 - 4(1)(300)}}{2(1)} \] \[ = \frac{35 \pm \sqrt{1225 - 1200}}{2} = \frac{35 \pm \sqrt{25}}{2} \] \[ W = \frac{35 \pm 5}{2} \Rightarrow W = 20 \text{ or } W = 15 \] For \( W = 15 \), \( L = 35 - 15 = 20 \).
For \( W = 20 \), \( L = 35 - 20 = 15 \).
Sine \( L \gt W \), the rectangle has dimensions \( L = 20 \) and \( W = 15 \).
Question 17
An electric motor makes 3,000 revolutions per minute. How many degrees does it rotate in one second?
The has a speed of \( 3000 \) revolutions per minute.
1 revolution is \( 360^\circ \)
1 minute is 60 second
Use abbreviations: min for minutes and rev for revolution to write: \[ \dfrac{3000 \text{rev}}{1 \text{min} } = \frac{3000 \, \text{rev}}{1 \, \text{min}} \times \frac{360^\circ}{1 \, \text{rev}} \times \frac{1 \, \text{min}}{60 \, \text{sec}} \] Cancel the units rev and min \[ = \frac{3000 \times 360}{60} \\ = \frac{1,080,000}{60} \\ = 18,000^\circ \, \text{per second} \] The motor rotates \( 18,000^\circ \) in one second.
Question 18
A real estate agent received a 6% commission on the selling price of a house. If his commission was \( \$ 8,880 \), what was the selling price of the house?
Let \( x \) be the selling price of the house. \[ 6\% \text{ of } x = 8,880 \] \[ 0.06x = 8,880 \] Solve for \( x \) \[ x = \frac{8,880}{0.06} \] \[ x = 148,000 \] The selling price of the house was \( \$148,000 \).
Question 19
If a tire rotates at \( 400 \) revolutions per minute when the car is traveling at \( 72 \) km/h, what is the circumference \( C \) of the tire?
We are given:
Rotational speed: \( 400 \, \text{rev/min} \)
Linear speed: \( 72 \, \text{km/h} = 72,000 \, \text{m/h} \)
First, convert revolutions per minute to revolutions per hour: \[ 400 \, \dfrac{\text{rev}}{\text{min}} \times 60 \, \dfrac{\text{min}}{\text{h}} = 24{,}000 \, \dfrac{\text{rev}}{\text{h}} \] Let \( C \) be the circumference of the tire in meters. The total distance traveled in one hour is also equal to the number of revolutions per hour multiplied by the circumference: \[ 24,000 \cdot C = 72,000 \] Solving for \( C \): \[ C = \frac{72,000}{24,000} = 3 \, \text{meters} \]
Question 20
In a shop, the cost of 4 shirts, 4 pairs of trousers, and 2 hats is \( \$560 \). The cost of 9 shirts, 9 pairs of trousers, and 6 hats is \( \$1,290 \). What is the total cost of 1 shirt, 1 pair of trousers, and 1 hat ?
Let: \( x \) be the cost of one shirt , \( y \) be the cost of one pair of trousers and \( z \) the cost of one hat We are given: \[ \begin{aligned} \text{(1)} &\quad 4x + 4y + 2z = 560 \\ \text{(2)} &\quad 9x + 9y + 6z = 1290 \end{aligned} \] Divide equation (2) by 3: \[ \text{(3)} \quad 3x + 3y + 2z = 430 \] Now subtract equation (1) from equation (3): \[ (3x + 3y + 2z) - (4x + 4y + 2z) = 430 - 560 \] \[ - x - y = -130 \quad \Rightarrow \quad x + y = 130 \quad \text{(4)} \] Substitute equation (4) into equation (3): \[ 3(x + y) + 2z = 430 \] \[ 3(130) + 2z = 430 \] \[ 390 + 2z = 430 \] \[ 2z = 40 \quad \Rightarrow \quad z = 20 \] Now substitute back to find total cost of 1 shirt, 1 pair of trousers, and 1 hat: \[ x + y + z = 130 + 20 = 150 \] The total cost of one shirt, one pair of trousers, and one hat is \( \$150 \).
Question 21
Four children have small toys. The first child has \( \frac{1}{10} \) of the toys, the second child has 12 more toys than the first, the third child has one more toy than the first child, and the fourth child has double the number of toys of the third child. How many toys are there?
Let \( x \) represent the total number of toys.
The first child has \( \frac{x}{10} \) toys.
The second child has \( \frac{x}{10} + 12 \) toys.
The third child has \( \frac{x}{10} + 1 \) toys.
The fourth child has \( 2 \left( \frac{x}{10} + 1 \right) \) toys.
We set up the equation for the total number of toys: \[ \frac{x}{10} + \left( \frac{x}{10} + 12 \right) + \left( \frac{x}{10} + 1 \right) + 2 \left( \frac{x}{10} + 1 \right) = x \] Expand: \[ \frac{x}{10} + \frac{x}{10} + 12 + \frac{x}{10} + 1 + \frac{2 x}{10} + 2 = x \] Combine like terms: \[ \frac{6x}{10} + 15 = x \] Multiply through by 10 to eliminate the denominator: \[ 5x + 150 = 10x \] Subtract \( 5x \) from both sides: \[ 150 = 5 x \] Solve for \( x \): \[ x = \frac{150}{5} = 30 \] Thus, the total number of toys is \( 30 \).
Question 22
Evaluate the expression: \[ \left( 1 - \frac{1}{10} \right) \left( 1 - \frac{1}{11} \right) \left( 1 - \frac{1}{12} \right) \cdots \left( 1 - \frac{1}{100} \right) \]
First, we write each term in the product as a fraction: \[ \left( 1 - \frac{1}{10} \right) \left( 1 - \frac{1}{11} \right) \left( 1 - \frac{1}{12} \right) \cdots \left( 1 - \frac{1}{100} \right) \] This becomes: \[ \left( \frac{9}{10} \right) \left( \frac{10}{11} \right) \left( \frac{11}{12} \right) \cdots \left( \frac{99}{100} \right) \] Now, observe the cancellation pattern. Most terms cancel out, leaving: \[ \frac{9}{100} \] Thus, the final answer is: \[ \frac{9}{100} \]