¿Cómo encontrar la inversa de una relación dada por su gráfica? Se presentan ejemplos junto con soluciones detalladas y también se incluyen preguntas con soluciones y explicaciones.
Un punto (par ordenado) en la gráfica de la inversa de una relación se obtiene intercambiando las coordenadas de un punto (par ordenado) en la gráfica de la relación. Geométricamente, un punto \( (a,b) \) en la gráfica de una relación y un punto correspondiente \( (b,a) \) en la inversa de la relación son reflejos el uno del otro sobre la recta \( y = x \).
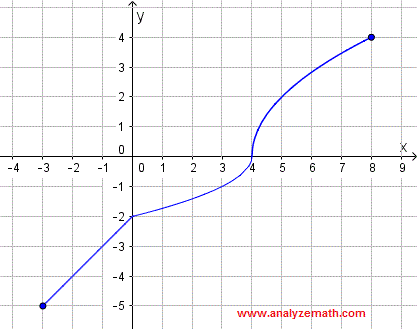
Dibuja la gráfica de la inversa de la relación dada por su gráfica a continuación.

Paso 1: Selecciona puntos en la gráfica de la relación dada y encuentra sus coordenadas \( (a,b) \). Los puntos seleccionados están marcados en azul en la gráfica a continuación con las siguientes coordenadas:
\( (8, 4),\ (5, 2),\ (4, 0),\ (3, -1),\ (0, -2),\ (-2, -4),\ (-3, -5) \)
Paso 2: Refleja los puntos sobre la recta \( y = x \) intercambiando las coordenadas \( x \) e \( y \). Los puntos reflejados (en rojo): \( (b,a) \) son:
\( (4, 8),\ (2, 5),\ (0, 4),\ (-1, 3),\ (-2, 0),\ (-4, -2),\ (-5, -3) \)

Dibuja la gráfica de la inversa de la relación dada conectando los puntos reflejados mostrados en rojo. La gráfica original y su inversa son imágenes especulares entre sí sobre la recta \( y = x \).

Dibuja la gráfica de la inversa de la relación dada por su gráfica a continuación.

Paso 1: Selecciona y define puntos en la gráfica de la relación dada por sus coordenadas \( (a,b) \) como se muestra en la gráfica a continuación (puntos azules en la gráfica).
Los puntos seleccionados son: \( (6, 3),\ (2, -5),\ (0, -1),\ (-2, -5),\ (-3, -3) \)
Paso 2: Refleja los puntos sobre la recta \( y = x \) intercambiando las coordenadas \( x \) e \( y \), como se muestra por los puntos rojos con coordenadas \( (b,a) \).
Puntos reflejados: \( (3, 6),\ (-5, 2),\ (-1, 0),\ (-5, -2),\ (-3, -3) \)

La gráfica de la relación inversa se obtiene conectando los puntos reflejados. La gráfica original y su inversa son imágenes especulares entre sí sobre la recta \( y = x \).

Dibuja la gráfica de la inversa de cada una de las relaciones dadas por su gráfica a continuación:
a)

b)

a)
Paso 1: Selecciona puntos en la gráfica de la relación dada y encuentra sus coordenadas: puntos azules mostrados en la gráfica a continuación con las siguientes coordenadas:
\( (4, 2),\ (2, 2),\ (1, -1),\ (0, -2),\ (-1, -1),\ (-2, -4) \)
Paso 2: Refleja sobre la recta \( y = x \) intercambiando las coordenadas \( x \) e \( y \) de los puntos obtenidos anteriormente para obtener los puntos rojos:
\( (2, 4),\ (2, 2),\ (-1, 1),\ (-2, 0),\ (-1, -1),\ (-4, -2) \)

La inversa de la relación dada se obtiene conectando los puntos invertidos como se muestra en la gráfica roja a continuación. La gráfica dada y la inversa son reflejos entre sí sobre la recta \( y = x \).

b)
Paso 1: Selecciona puntos en la gráfica de la relación dada y encuentra sus coordenadas. Los puntos azules se muestran en la gráfica a continuación con las siguientes coordenadas:
\[(5, 6), \quad (4, 1), \quad (2, -1), \quad (0, -3), \quad (-1, -8)\]
Paso 2: Refleja los puntos (intercambiando las coordenadas \( x \) e \( y \)) sobre la recta \( y = x \). Estos se muestran como puntos rojos:
\[(6, 5), \quad (1, 4), \quad (-1, 2), \quad (-3, 0), \quad (-8, -1)\]

Dibuja la gráfica de la inversa de la relación dada conectando los puntos invertidos como se muestra en la gráfica roja a continuación, de modo que la gráfica dada y la inversa sean reflejos entre sí sobre la recta \( y = x \).
