
¿Cómo resolver ecuaciones trigonométricas? Se presentan preguntas junto con soluciones y explicaciones detalladas.
Encuentra todas las soluciones de la ecuación trigonométrica \[ \sqrt{3} \sec(\theta) + 2 = 0\]
Usando la identidad \(\sec(\theta) = \dfrac{1}{\cos(\theta)}\), reescribimos la ecuación en la forma \[ \cos(\theta) = -\dfrac{\sqrt{3}}{2} \] Encuentra el ángulo de referencia \(\theta_r\) resolviendo la ecuación sin el signo negativo: \[ \cos(\theta_r) = \dfrac{\sqrt{3}}{2} \] donde \(\theta_r\) es agudo e igual al ángulo de referencia. La solución a la ecuación \(\cos(\theta_r) = \dfrac{\sqrt{3}}{2}\) es: \[ \theta_r = \dfrac{\pi}{6} \] Usa el ángulo de referencia \(\theta_r\) para determinar las soluciones \(\theta_1\) y \(\theta_2\) en el intervalo \([0, 2\pi)\). La ecuación \(\cos(\theta) = -\dfrac{\sqrt{3}}{2}\) indica que \(\cos(\theta)\) es negativo, lo que significa que el lado terminal del ángulo \(\theta\) está en los cuadrantes II o III, como se muestra en el círculo unitario.

Por lo tanto, las soluciones en el intervalo \([0, 2\pi)\) son: \[ \theta_1 = \pi - \theta_r = \pi - \dfrac{\pi}{6} = \dfrac{5\pi}{6} \] \[ \theta_2 = \pi + \theta_r = \pi + \dfrac{\pi}{6} = \dfrac{7\pi}{6} \] Usa las soluciones en el intervalo \([0, 2\pi)\) para encontrar todas las soluciones sumando múltiplos de \(2\pi\): \[ \theta_1 = \dfrac{5\pi}{6} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \] \[ \theta_2 = \dfrac{7\pi}{6} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \] A continuación se muestran las soluciones gráficas en el intervalo \([0, 2\pi)\):

Resuelve la ecuación trigonométrica \[ 2 \sin(\theta) = -1 \]
Reescribe la ecuación en forma simple: \[ \sin(\theta) = -\dfrac{1}{2} \] Encuentra el ángulo de referencia \(\theta_r\) resolviendo la ecuación sin el signo negativo: \[ \sin(\theta_r) = \dfrac{1}{2} \] \(\theta_r\) es agudo e igual a: \[ \theta_r = \dfrac{\pi}{6} \] Usa el ángulo de referencia \(\theta_r\) para determinar las soluciones \(\theta_1\) y \(\theta_2\) en el intervalo \([0, 2\pi)\). La ecuación \(\sin(\theta) = -\dfrac{1}{2}\) indica que \(\sin(\theta)\) es negativo, por lo que el lado terminal del ángulo \(\theta\) está en los cuadrantes III o IV.
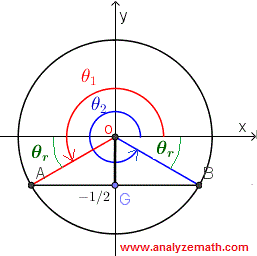
Por lo tanto, las soluciones son: \[ \theta_1 = \pi + \theta_r = \pi + \dfrac{\pi}{6} = \dfrac{7\pi}{6} \] \[ \theta_2 = 2\pi - \theta_r = 2\pi - \dfrac{\pi}{6} = \dfrac{11\pi}{6} \] Usa las soluciones en el intervalo \([0, 2\pi)\) para encontrar todas las soluciones sumando múltiplos de \(2\pi\): \[ \theta_1 = \dfrac{7\pi}{6} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \] \[ \theta_2 = \dfrac{11\pi}{6} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \]
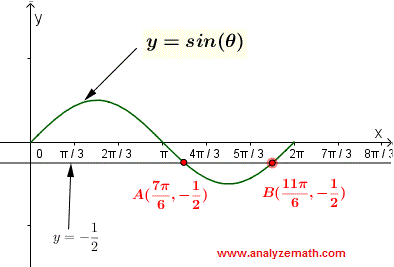
Resuelve la ecuación trigonométrica \[ \sqrt{2} \cos\left(3x + \dfrac{\pi}{4}\right) = -1 \]
Sea \(\theta = 3x + \dfrac{\pi}{4}\) y reescribe la ecuación en forma simple: \[ \sqrt{2} \cos(\theta) = -1 \] \[ \cos(\theta) = -\dfrac{1}{\sqrt{2}} \] Encuentra el ángulo de referencia \(\theta_r\) resolviendo \(\cos(\theta_r) = \dfrac{1}{\sqrt{2}}\) para \(\theta_r\) agudo: \[ \theta_r = \dfrac{\pi}{4} \] Usa el ángulo de referencia \(\theta_r\) para determinar las soluciones \(\theta_1\) y \(\theta_2\) en el intervalo \([0, 2\pi)\). La ecuación \(\cos(\theta) = -\dfrac{1}{\sqrt{2}}\) indica que \(\cos(\theta)\) es negativo, por lo que el lado terminal del ángulo \(\theta\) está en los cuadrantes II o III. Las dos soluciones en el intervalo \([0, 2\pi)\) son: \[ \theta_1 = \pi - \theta_r = \pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4} \] \[ \theta_2 = \pi + \theta_r = \pi + \dfrac{\pi}{4} = \dfrac{5\pi}{4} \] Escribe las soluciones generales sumando múltiplos de \(2\pi\): \[ \theta_1 = \dfrac{3\pi}{4} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \] \[ \theta_2 = \dfrac{5\pi}{4} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \] Sustituye \(\theta_1\) y \(\theta_2\) por la expresión \(3x + \dfrac{\pi}{4}\): \[ 3x + \dfrac{\pi}{4} = \dfrac{3\pi}{4} + 2n\pi \] \[ 3x + \dfrac{\pi}{4} = \dfrac{5\pi}{4} + 2n\pi \] y resuelve para \(x\): \[ x_1 = \dfrac{\pi}{6} + \dfrac{2n\pi}{3}, \quad n = 0, \pm 1, \pm 2, \ldots \] \[ x_2 = \dfrac{\pi}{3} + \dfrac{2n\pi}{3}, \quad n = 0, \pm 1, \pm 2, \ldots \]
Resuelve la ecuación trigonométrica \[ - 2 \sin^2 x - \cos x = - 1 \]
La ecuación puede factorizarse si todas las funciones trigonométricas son iguales. Usando la identidad \(\sin^2 x = 1 - \cos^2 x\), reescribe la ecuación usando la misma función trigonométrica \(\cos x\): \[ - 2 (1 - \cos^2 x) - \cos x = - 1 \] Simplifica y reescribe: \[ 2 \cos^2 x - \cos x - 1 = 0 \] Factoriza el lado izquierdo: \[ (2 \cos x + 1)(\cos x - 1) = 0 \] Por lo tanto, hay dos ecuaciones por resolver: \[ (1) \quad 2 \cos x + 1 = 0 \quad \text{y} \quad (2) \quad \cos x - 1 = 0 \] Resuelve la ecuación (1): \[ \cos x = -\dfrac{1}{2} \] \[ x_1 = \dfrac{2\pi}{3} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \] \[ x_2 = \dfrac{4\pi}{3} + 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \] Resuelve la ecuación (2): \[ \cos x = 1 \] \[ x_3 = 2n\pi, \quad n = 0, \pm 1, \pm 2, \ldots \]