Problemas de Geometría con Soluciones para Grado 12

El triángulo \( ABC \) tiene dos lados con igual longitud y, por lo tanto, es un triángulo isósceles con base AC. La medida del ángulo \( \angle BAC \) está dada por:

\[ \angle BAC = \dfrac{180^\circ - 36^\circ}{2} = 72^\circ \]

El ángulo \( \angle BOC \) es un ángulo central y \( \angle BAC \) es un ángulo inscrito; ambos interceptan el mismo arco, por lo tanto:

\[ \text{Medida de } \angle BOC = 2 \times \text{Medida de } \angle BAC = 144^\circ \]

Sean \( R_1, \; R_2 \) y \( R_3 \) los radios de las circunferencias C1, C2 y C3, con \( R_1 = R_2 = R \).

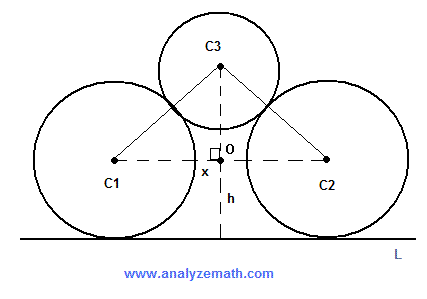
Sea \( C3O \) la distancia desde C3 al segmento C1C2. Por lo tanto:

\[ h = C3O + R \quad (I) \]

Aplicando el teorema de Pitágoras al triángulo C3 O C1:

\[ C3O^2 + \left(\dfrac{x}{2}\right)^2 = (R + R_3)^2 \]

lo que da:

\[ C3O = \sqrt{(R + R_3)^2 - \left(\dfrac{x}{2}\right)^2} \]

Usando (I), obtenemos:

\[ h = R + C_3O = R + \sqrt{(R + R_3)^2 - \left(\dfrac{x}{2}\right)^2} \]

Sean \( r \), \( R_2 \), y \( R_3 \) los radios de las circunferencias \( C1 \), \( C2 \), y \( C3 \) respectivamente, con \( R_2 = R_3 = R \).

Teorema de Pitágoras en el triángulo \( M C1 C3 \):

\[ C1C3^2 = MC3^2 + MC1^2 \quad (I) \]

Sustituyendo: \(C1C3 = r+R , \; MC3 = R , \; MC1 = R - r \) en \( (I) \):

Expandir, simplificar y resolver para \( R \):

\[ R = 4r = 40 \text{ cm} \]

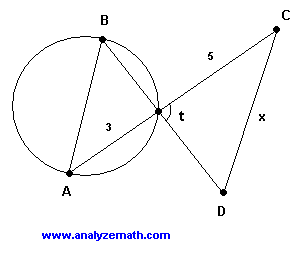
Los ángulos \( \angle BtA \) y \( \angle CtD \) son opuestos por el vértice, por lo tanto:

\[ \angle BtA = 90^\circ \]

Como \( \angle BtA = 90^\circ \), \( AB \) es el diámetro de la circunferencia (converso del teorema de Tales).

Como \( CD \) es paralelo a \( AB \), los triángulos \( BtA \) y \( CtD \) son semejantes, por lo que la proporcionalidad de lados correspondientes da:

\[ \dfrac{3}{5} = \dfrac{AB}{x} \]

Resolviendo para el diámetro \( AB \):

\[ AB = \dfrac{3x}{5} \] \[ \text{radio} = \dfrac{AB}{2} = \dfrac{3x}{10} \] \[ \text{área} = \pi \times \text{radio}^2 = \pi \left(\dfrac{3x}{10}\right)^2 = 0.09 \pi x^2 \]

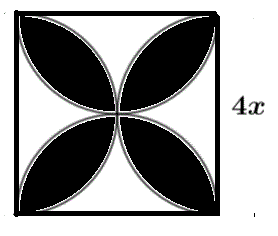
Dividamos el cuadrado grande en cuatro cuadrados pequeños como se muestra.

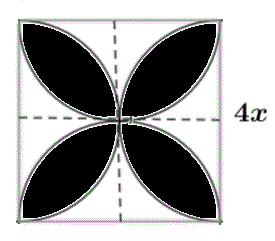
Consideremos un cuadrado pequeño, por ejemplo el inferior izquierdo. Este cuadrado tiene lado \( 2x \). Parte de él está sombreada y parte no. Encontremos el área de la parte no sombreada (blanca). La parte sombreada es un cuarto de círculo.

\[ \text{Área no sombreada} = \text{área del cuadrado} - \frac{1}{4} \text{área del círculo} = (2x)^2 - \dfrac{1}{4} \pi (2x)^2 \]

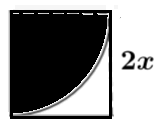
En la figura del problema 5, el área total no sombreada es 8 veces el área no sombreada del cuadrado pequeño:

El área \( A \) de la parte sombreada en el problema 5 es:

\[ A = \text{Área total del cuadrado grande} - \text{Área total no sombreada} \] \[ = (4x)^2 - 8 \left[ (2x)^2 - \dfrac{1}{4} \pi (2x)^2 \right] \] \[ = 16x^2 \left( \dfrac{\pi}{2} - 1 \right) \]

El triángulo rectángulo en la imagen tiene hipotenusa \( R \), un cateto \( r \) y el otro cateto igual a la mitad de la cuerda: \( 20 / 2 \) mm.

Usando el teorema de Pitágoras:

\[ R^2 = r^2 + 10^2 \quad (I) \]

El área \( A \) del anillo se encuentra restando el área de la circunferencia pequeña a la grande:

\[ A = \pi (R^2 - r^2) \quad (II) \]

De la ecuación \( I \):

\[ R^2 - r^2 = 10^2 = 100 \]

Sustituyendo en \( II \):

\[ A = 100 \pi \]

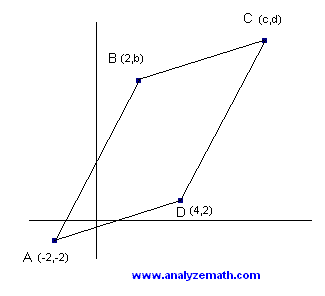
El área de un paralelogramo puede calcularse usando el producto cruz de los vectores \(\mathbf{AB}\) y \(\mathbf{AD}\):

\[ \text{Área} = \left| \mathbf{AB} \times \mathbf{AD} \right| \]

donde \(\mathbf{AB}\) y \(\mathbf{AD}\) son vectores tridimensionales con componente \( z \) igual a cero para poder calcular el producto cruz.

Calculamos los vectores:

\[ \mathbf{AB} = \langle 2 - (-2) , b - (- 2), 0 - 0 \rangle = \langle 4 , b +2, 0 \rangle \] \[ \mathbf{AD} = \langle 4-(-2), 2 - (-2) , 0 \rangle = \langle 6, 4, 0 \rangle \]

Calculando la magnitud del producto cruz:

\[ \left| \langle 4, b+2, 0 \rangle \times \langle 6, 4, 0 \rangle \right| = 80 \]

El producto cruz en forma de determinante:

\[ \mathbf{AB} \times \mathbf{AD} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 4 & b+2 & 0 \\ 6 & 4 & 0 \end{vmatrix} \]

Expandiendo:

\[ = \mathbf{i} \begin{vmatrix} b+2 & 0 \\ 4 & 0 \end{vmatrix} - \mathbf{j} \begin{vmatrix} 4 & 0 \\ 6 & 0 \end{vmatrix} + \mathbf{k} \begin{vmatrix} 4 & b+2 \\ 6 & 4 \end{vmatrix} \]

Obtenemos:

\[ \mathbf{AB} \times \mathbf{AD} = (4 - 6b) \mathbf{k} \]

Tomando magnitud:

\[ |4 - 6b| = 80 \]

Resolviendo para \( b \):

\[ 4 - 6b = 80 \quad \text{o} \quad 4 - 6b = -80 \] \[ b = -\dfrac{38}{3}, \quad b = 14 \]

Como el punto \( B(2, b) \) está en el primer cuadrante, elegimos \( b = 14 \).

Como \( ABCD \) es paralelogramo:

\[ \mathbf{AB} = \mathbf{DC} \]

Entonces:

\[ \mathbf{AB} = \langle 4, 16, 0 \rangle \] \[ \mathbf{DC} = \langle c - 4, d - 2, 0 \rangle \]

Igualando componentes:

\[ c - 4 = 4, \quad d - 2 = 16 \]

Resolviendo:

\[ c = 8, \quad d = 18 \]

Por lo tanto: \( b = 14 \), \( c = 8\), \( d = 18 \).

Hay 3 triángulos rectángulos. Usando el teorema de Pitágoras:

\[ y^2 + z^2 = 12^2 \quad (I) \] \[ x^2 + z^2 = 9^2 \quad (II) \] \[ (y + x)^2 = 12^2 + 9^2 = 225 \quad (III) \]

Resolviendo \( (III) \):

\[ x + y = 15 \]

Restando \( (II) \) de \( (I) \):

\[ y^2 - x^2 = 12^2 - 9^2 = 63 \quad (IV) \]

Factorizando:

\[ (y - x)(y + x) = 63 \]

Sustituyendo \( x + y = 15 \):

\[ y - x = \dfrac{21}{5} \]

Resolviendo el sistema:

\[ \begin{cases} x + y = 15 \\ y - x = \dfrac{21}{5} \end{cases} \]

Obtenemos \( x = \dfrac{27}{5} \), \( y = \dfrac{48}{5} \).

Usando \( (I) \) para encontrar \( z \):

\[ \left(\dfrac{48}{5}\right)^2 + z^2 = 12^2 \] \[ z^2 = 12^2 - \left(\dfrac{48}{5}\right)^2 = \dfrac{1296}{25} \]

Por lo tanto:

\[ z = \dfrac{36}{5} \]

Los valores son:

\[ x = \dfrac{27}{5}, \quad y = \dfrac{48}{5}, \quad z = \dfrac{36}{5} \]

Dividamos el rectángulo en 4 rectángulos como se muestra.

Teorema de Pitágoras en el triángulo superior izquierdo:

\[ a^2 + c^2 = 4^2 \quad (I) \]

En el triángulo inferior izquierdo:

\[ b^2 + c^2 = x^2 \quad (II) \]

En el triángulo inferior derecho:

\[ b^2 + d^2 = 5^2 \quad (III) \]

En el triángulo superior derecho:

\[ a^2 + d^2 = 6^2 \quad (IV) \]

Restando \( (II) \) de \( (I) \):

\[ a^2 - b^2 = 4^2 - x^2 \]

Restando \( (III) \) de \( (IV) \):

\[ a^2 - b^2 = 6^2 - 5^2 \]

Igualando:

\[ 4^2 - x^2 = 6^2 - 5^2 \]

Resolviendo para \( x \):

\[ x = \sqrt{5} \]

Por simetría, la región sombreada puede considerarse como dos regiones iguales. El área de la mitad izquierda es el área del sector \( BOC \) menos el área del triángulo \( BOC \).

Como la distancia entre centros es 6, la longitud de \( OM \) es:

\[ OM = 6/2 = 3 \]

El triángulo \( BOM \) es rectángulo, entonces:

\[ \cos \angle BOM = \dfrac{OM}{OB} = \dfrac{3}{4} \] \[ \angle BOM = \arccos\left(\dfrac{3}{4}\right) \]

Área del sector \( BOC \):

\[ \text{Área sector } BOC = \dfrac{1}{2} (2 \angle BOM ) r^2 \]

Área del triángulo \( BOC \):

\[ \text{Área triángulo } BOC = \dfrac{1}{2} \sin(2 \angle BOM ) r^2 \]

Área total sombreada:

\[ 2 \left[ \dfrac{1}{2} (2 \angle BOM) r^2 - \dfrac{1}{2} \sin(2 \angle BOM ) r^2 \right] \]

Sustituyendo \( \angle BOM = \arccos\left(\dfrac{3}{4}\right) \) y \( r = 4 \):

\[ = \left(2 \arccos\left(\dfrac{3}{4}\right) - \sin \left(2 \arccos\left(\dfrac{3}{4}\right) \right) \right) 4^2 \] \[ \approx 7.25 \text{ unidades cuadradas} \quad \text{(redondeado a 3 decimales)} \]