
¿Quieres dominar las ecuaciones exponenciales? Esta guía ofrece a estudiantes de 12º grado soluciones claras y detalladas usando métodos analíticos y gráficos. Aprenderás técnicas poderosas como la sustitución y las reglas de funciones exponenciales y logarítmicas para resolver ecuaciones complejas con confianza.
También mostramos cómo resolver ecuaciones exponenciales gráficamente. Para ello, primero reescribimos la ecuación en la forma \( f(x) - g(x) = 0 \). Luego, graficamos la función \( f(x) - g(x) \), y las intersecciones con el eje x representan las soluciones de la ecuación original.
Ya sea que te estés preparando para exámenes o solo quieras fortalecer tus habilidades matemáticas, este recurso te ayudará a comprender y resolver ecuaciones exponenciales paso a paso.
Observa que 27, 9 y 3 pueden escribirse como potencias de 3 de la siguiente manera:
\[ 27 = 3^3, \quad 9 = 3^2, \quad \text{y} \quad 3 = 3^1\]Usando lo anterior y también la fórmula para exponentes negativos:
\[ \dfrac{1}{x^n} = x^{-1} \]Reescribimos la ecuación dada de la siguiente manera:
\[ (3^3)^{2x} \cdot (3^{-2})^{x - 2} = (3^2)^{-x} \cdot (3^{-1})^{2 - x} \]Ahora usamos la fórmula \((x^m)^n = x^{mn}\) para reescribir la ecuación anterior:
\[ 3^{6x} \cdot 3^{-2x + 4} = 3^{-2x} \cdot 3^{-2 + x} \]Usa la fórmula \(x^m \cdot x^n = x^{m + n}\) para reescribir la ecuación:
\[ 3^{6x - 2x + 4} = 3^{-2x - 2 + x} \]Simplifica los exponentes:
\[ 3^{4x + 4} = 3^{-x - 2} \]Usamos el hecho de que la función exponencial de la forma \(a^x\) es uno a uno, lo que significa que si \(3^m = 3^n\), entonces \(m = n\) para escribir una ecuación algebraica:
\[ 4x + 4 = -x - 2 \]Resuelve para \(x\):
\[ 5x = -6 \quad \text{da la solución} \quad x = \dfrac{-6}{5} = -1.2 \]A continuación se muestra la gráfica del lado izquierdo de la ecuación dada cuando se escribe con el lado derecho igual a cero:
\[ 27^{2x} \left(\dfrac{1}{9}\right)^{x-2} - 9^{-x} \left(\dfrac{1}{3}\right)^{2-x} = 0 \]La intersección con el eje x es una aproximación a la solución analítica encontrada anteriormente. Verifica que los valores sean cercanos.

Encuentra las soluciones de la ecuación:
\[ \sqrt{16^x} = \left( \dfrac{1}{2} \right)^{x^2-1} \]Observa que \( \sqrt{16^x} = (16^x)^{1/2} = 16^{(1/2)x} \) y úsalo para reescribir la ecuación dada:
\[ 16^{(1/2)x} = \left(\dfrac{1}{2}\right)^{x^2 - 1} \]Observa que \( \dfrac{1}{2} = 2^{-1} \) y \( 16 = 2^4 \) y úsalo para reescribir la ecuación anterior:
\[ (2^4)^{(1/2)x} = (2^{-1})^{x^2 - 1} \]Usa la fórmula \( (x^m)^n = x^{mn} \):
\[ 2^{2x} = 2^{-x^2 + 1} \]Usamos el hecho de que la función exponencial es uno a uno:
\[ 2x = -x^2 + 1 \]Reescribe en forma estándar y resuelve la ecuación cuadrática:
\[ x^2 + 2x - 1 = 0 \] \[ \Delta = 2^2 - 4(1)(-1) = 8 \]Dos soluciones: \( x_1 = -1 - \sqrt{2} \approx -2.41 \) y \( x_2 = -1 + \sqrt{2} \approx 0.41 \)
La gráfica del lado izquierdo de la ecuación dada cuando se escribe con el lado derecho igual a cero:
\[ \sqrt{16^x} - \left( \dfrac{1}{2} \right)^{x^2-1} = 0 \]se muestra a continuación. Las intersecciones con el eje x son aproximaciones a las soluciones analíticas.

¿Cuáles son las soluciones de la ecuación?
\[ 2^x - 6 \cdot 2^{-x} = 6 \]Sea \( u = 2^x \) lo que también da \( \dfrac{1}{u} = 2^{-x} \), y reescribe la ecuación en términos de \( u \):
\[ u - \dfrac{6}{u} = 6 \]Como \( u \) no puede ser cero (porque \( 2^x \) no puede ser menor o igual a cero), multiplicamos todos los términos por \( u \):
\[ u^2 - 6 = 6u \] \[ u^2 - 6u - 6 = 0 \]Resuelve la ecuación cuadrática para \( u \):
\[ u_1 = 3 + \sqrt{15} \quad \text{y} \quad u_2 = 3 - \sqrt{15} \]Ahora resolvemos para \( x \) usando la sustitución \( u = 2^x \).
Primera ecuación: \( 2^x = 3 + \sqrt{15} \)
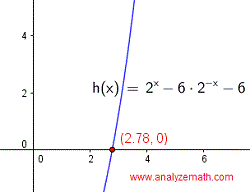
\[ \ln(2^x) = \ln(3 + \sqrt{15}) \] \[ x \ln(2) = \ln(3 + \sqrt{15}) \] \[ x = \dfrac{\ln(3 + \sqrt{15})}{\ln 2} \approx 2.78 \]Segunda ecuación: \( 2^x = 3 - \sqrt{15} \) no tiene solución porque \( 3 - \sqrt{15} \) es menor que cero.
A continuación se muestra la gráfica de la ecuación escrita como \( 2^x - 6 \cdot 2^{-x} - 6 = 0 \). La intersección con el eje x aproxima la solución analítica.
Encuentra las soluciones de la ecuación:
\[ 5^{x+1} = 100 \cdot 3^x \]Aplica logaritmo natural (ln) a ambos lados:
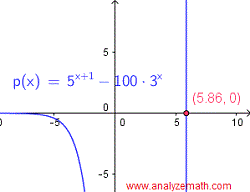
\[ \ln(5^{x + 1}) = \ln(100 \cdot 3^x) \] \[ (x + 1) \ln 5 = \ln 100 + x \ln 3 \] \[ x \ln 5 + \ln 5 = \ln 100 + x \ln 3 \] \[ x (\ln 5 - \ln 3) = \ln 100 - \ln 5 \] \[ x = \dfrac{\ln 100 - \ln 5}{\ln 5 - \ln 3} \approx 5.86 \]Gráfica de \( 5^{x+1} - 100 \cdot 3^x = 0 \):
Resuelve la ecuación:
\[ \dfrac{e^x - e^{-x}}{2} = 3 \]Sea \( u = e^x \), entonces \( \dfrac{1}{u} = e^{-x} \):
\[ \dfrac{u - \dfrac{1}{u}}{2} = 3 \] \[ u - \dfrac{1}{u} = 6 \] \[ u^2 - 1 = 6u \] \[ u^2 - 6u - 1 = 0 \]Soluciones para \( u \):
\[ u_1 = 3 + \sqrt{10} \quad \text{y} \quad u_2 = 3 - \sqrt{10} \]Resolvemos para \( x \) con \( u = e^x \).
Primera ecuación: \( e^x = 3 + \sqrt{10} \)
\[ x = \ln(3 + \sqrt{10}) \approx 1.82 \]Segunda ecuación: \( e^x = 3 - \sqrt{10} \) no tiene solución.
Gráfica de \( \dfrac{e^x - e^{-x}}{2} - 3 = 0 \):

¿Cuáles son las soluciones de la ecuación?
\[ 3^{2-3x} = 4^{2x+1} \]Aplica logaritmo natural a ambos lados:
\[ \ln(3^{2 - 3x}) = \ln(4^{2x + 1}) \] \[ (2 - 3x)\ln 3 = (2x + 1)\ln 4 \] \[ 2\ln 3 - 3x\ln 3 = 2x\ln 4 + \ln 4 \] \[ x(-3\ln 3 - 2\ln 4) = \ln 4 - 2\ln 3 \] \[ x = \dfrac{2\ln 3 - \ln 4}{3\ln 3 + 2\ln 4} \approx 0.13 \]Gráfica de \( 3^{2-3x} - 4^{2x+1} = 0 \):

Resuelve para \( x \) la ecuación:
\[ 9^x - 3^{x + 1} + 2 = 0 \]Observa que \( 9^x = (3^x)^2 \) y \( 3^{x + 1} = 3 \cdot 3^x \):
\[ (3^x)^2 - 3 \cdot 3^x + 2 = 0 \]Sea \( u = 3^x \):
\[ u^2 - 3u + 2 = 0 \] \[ (u - 2)(u - 1) = 0 \]Soluciones: \( u_1 = 2 \) y \( u_2 = 1 \).
Resolvemos para \( x \):
Para \( 3^x = 2 \):
\[ x = \dfrac{\ln 2}{\ln 3} \approx 0.63 \]Para \( 3^x = 1 \): \( x = 0 \).
Gráfica de la ecuación original:
