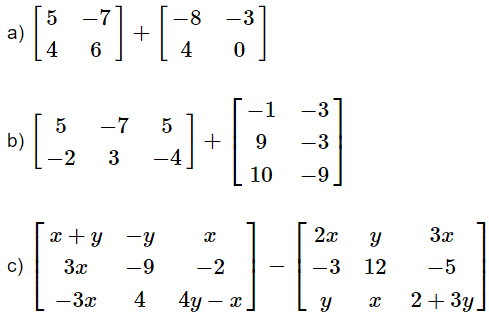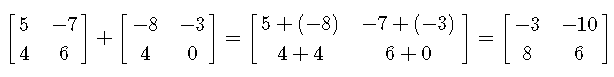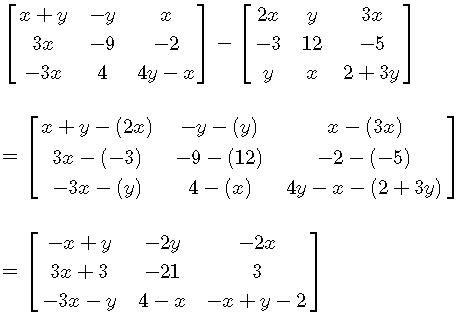Matrices de suma, resta y multiplicación escalar
Operaciones en Matrices como sumar, restar y multiplicar por un escalar junto con la igualdad de matrices se presentan mediante ejemplos y preguntas con soluciones.
Page Content
Sumar y Restar Matrices
Solo matrices
del mismo orden se pueden sumar o restar. Sumamos (o restamos) dos matrices sumando (o restando) sus entradas correspondientes.
Ejemplo 1
Reescribe, si es posible, cada una de las siguientes expresiones como una sola matriz.
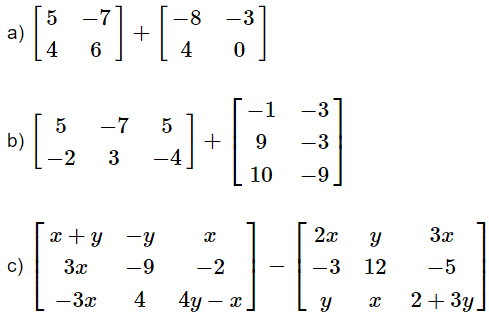
Solución
a) Las matrices del apartado a) tienen el mismo orden y por tanto podemos sumarlas sumando sus entradas correspondientes. Por eso
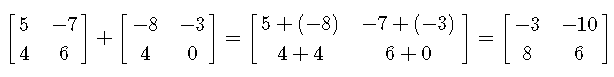
b) Las matrices del apartado b) no tienen el mismo orden y por tanto no podemos sumarlas.
c) Las matrices del inciso c) tienen el mismo orden y por tanto podemos sumarlas sumando sus entradas correspondientes y simplificando las expresiones algebraicas.
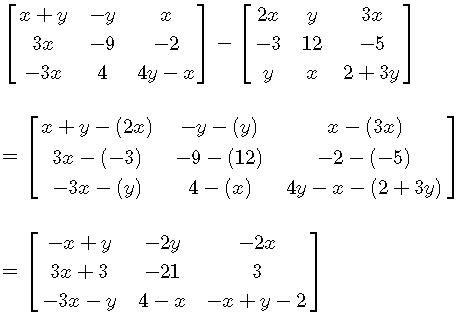
Multiplicar una matriz por un escalar
Para multiplicar una matriz por un escalar, multiplica todas las entradas de esa matriz por el escalar. Tenga en cuenta que la multiplicación escalar no cambia el orden de la matriz.
Ejemplo 2
Expresar como una sola matriz.
\( \)\( \)\( \)\( \)
a) - 5 \( \begin{bmatrix}
5 & - 7 \\
4 & 6
\end{bmatrix} \)
b) \( 2 \begin{bmatrix}
x & x + y & 6\\
-2 & - x & 1
\end{bmatrix} - 3 \begin{bmatrix}
- x & -2y & 0\\
3x & x & -1
\end{bmatrix} \)
Solución
a) - 5 \( \begin{bmatrix}
5 & - 7 \\
4 & 6
\end{bmatrix} = \begin{bmatrix}
-5(5) & -5(- 7) \\
-5(4) & -5(6)
\end{bmatrix}= \begin{bmatrix}
-25 & 35 \\
-20 & - 30
\end{bmatrix}\)
b) \( 2 \begin{bmatrix}
x & x + y & 6\\
-2 & - x & 1
\end{bmatrix} - 3 \begin{bmatrix}
- x & -2y & 0\\
3x & x & -1
\end{bmatrix} \)
Multiplica la primera matriz por 2 y la segunda matriz por 3
\( = \begin{bmatrix}
2(x) & 2(x + y) & 2(6)\\
2(-2) & 2(- x) & 2(1)
\end{bmatrix} - \begin{bmatrix}
3(-x) & 3(-2y) & 3(0)\\
3(3x) & 3(x) & 3(-1)
\end{bmatrix} = \)
Resta, agrupa y simplifica las expresiones algebraicas
\( = \begin{bmatrix}
5x & 2x+8y & 12\\
-4 - 9x & -5x & 5
\end{bmatrix}\)
Igualdad de dos Matrices
Dos matrices son iguales si tienen el mismo orden (igual número de filas e igual número de columnas) y sus correspondientes entradas son iguales.
Ejemplo 3
¿Cuáles de las siguientes matrices son iguales?
a) \(
\begin{bmatrix}
1 & 2 \\
3 & 4 \\
\end{bmatrix}
\),
b) \(
\begin{bmatrix}
x & 2x \\
2 & 1 \\
\end{bmatrix}
\),
c)
\(
\begin{bmatrix}
1 & -x \\
3x & 5 \\
\end{bmatrix}
\),
d)
\(
\begin{bmatrix}
1 & 2 \\
3 & 4 \\
\end{bmatrix}
\),
e)
\(
\begin{bmatrix}
1 & 2 & 5\\
3 & 4 & 8\\
\end{bmatrix}
\),
Solución
Las matrices a), b), c) yd) tienen el mismo orden 2 por 2. Pero solo las matrices a) yd) son iguales ya que tienen entradas correspondientes iguales. La matriz e) tiene el orden de 2 por 3 que es diferente al orden de todas las demás matrices y por lo tanto no es igual a ninguna de las matrices.
Ejemplo 4
Encuentre x y y para que
\[ \begin{bmatrix}
2x + y & - 7 \\
4 & 6
\end{bmatrix} = \begin{bmatrix}
2 & - 7 \\
4 & 4x + y
\end{bmatrix} \].
Solución
Las dos matrices tienen el mismo orden. Para que estas matrices sean iguales, todas sus entradas correspondientes tienen que ser iguales. Entradas correspondientes - 7 y 4 son iguales. Las entradas con las incógnitas x e y tienen que ser iguales. Por eso
2 x + y = 2 y 6 = 4 x + y
Resuelva el sistema de ecuaciones anterior para encontrar
x = 2 , y = - 2
Como ejercicio, sustituya x por 2 e y por - 2 en las matrices y verifique que sean iguales.
Preguntas sobre Matrices
Parte 1
Encuentre x e y, si es posible, tal que
A)
\(
\begin{bmatrix}
2x + y & 3 & 10 \\
y + 1 & -2 & 0 \\
\end{bmatrix}
= \begin{bmatrix}
2 & 3 & 10 \\
3 & -2 & 0 \\
\end{bmatrix} \)
B)
\( \begin{bmatrix}
6 & -4 & -6 & x - y
\end{bmatrix} = - 2 \begin{bmatrix}
-3 & 2 & 2x + 2y & 13
\end{bmatrix} \)
Parte 2
Escribir como una matriz
A) \( \begin{bmatrix}
-2 & 4 & 3 \\
-6 & 3 & -4 \\
-1 & 0 & 9 \\
\end{bmatrix}
+
\begin{bmatrix}
-1 & 0 & 23 \\
-4 & -3 & 9 \\
2 & -5 & 0 \\
\end{bmatrix}
\)
B) \( - 2 \begin{bmatrix}
-2 & 3 \\
1 & -5
\end{bmatrix} + 4 \begin{bmatrix}
3 & 4 \\
-2 & 9
\end{bmatrix} \)
C) \( -3 \begin{bmatrix}
-2x & y + 2 & 6\\
4 & - x & -4 \\
\end{bmatrix} + 5 \begin{bmatrix}
3x & 5y & -5\\
3y & x+y & -1
\end{bmatrix} \)
Soluciones a las preguntas
Parte 1
A)
The two matrices have the same order and to be equal, they need to have equal corresponding entries. Hence the simultaneous equations.
2x + y = 2 and y + 1 = 3
Las dos matrices tienen el mismo orden y, para ser iguales, deben tener entradas correspondientes iguales. De ahí las ecuaciones simultáneas.
2x + y = 2 y y + 1 = 3
Resuelva las ecuaciones anteriores para obtener: x = 0 y y = 2.
B)
Multiplique la segunda ecuación por -2 y reescriba la ecuación dada de la siguiente manera:
\( \begin{bmatrix}
6 & -4 & -6 & x - y
\end{bmatrix} = \begin{bmatrix}
6 & -4 & -2(2x + 2y) & -26 \end{bmatrix}\)
Para que las dos ecuaciones sean iguales, necesitamos tener
-2(2x + 2y) = - 6 y x - y = - 26
Resuelva el sistema anterior para obtener: x = -49/4 y y = 55/4
Parte 2
A) \( \begin{bmatrix}
-2 & 4 & 3 \\
-6 & 3 & -4 \\
-1 & 0 & 9
\end{bmatrix}
+
\begin{bmatrix}
-1 & 0 & 23 \\
-4 & -3 & 9 \\
2 & -5 & 0
\end{bmatrix} = \begin{bmatrix}-3&4&26\\ -10&0&5\\ 1&-5&9\end{bmatrix}
\)
B) \( - 2 \begin{bmatrix}
-2 & 3 \\
1 & -5
\end{bmatrix} + 4 \begin{bmatrix}
3 & 4 \\
-2 & 9
\end{bmatrix} = \begin{bmatrix}16&10\\ -10&46\end{bmatrix}\)
C) \( -3 \begin{bmatrix}
-2x & y + 2 & 6\\
4 & - x & -4
\end{bmatrix} + 5 \begin{bmatrix}
3x & 5y & -5\\
3y & x+y & -1
\end{bmatrix} = \begin{bmatrix}21x&22y-6&-43\\ -12+15y&8x+5y&7\end{bmatrix}\)
Más referencias y enlaces