Un auto viajó 281 millas en 4 horas y 41 minutos. ¿Cuál fue la velocidad promedio del auto en millas por hora?
Solución
Primero convertimos el tiempo de 4 horas 41 minutos a minutos:
4 horas 41 minutos = 4 × 60 + 41 = 281 minutos
La velocidad promedio S está dada por distancia / tiempo. Por lo tanto:
S = 281 millas / 281 minutos = 1 milla / minuto = 60 millas / hora
En un grupo de 120 personas, 90 tienen una edad mayor a 30 años, y las demás tienen una edad menor a 20 años. Si se selecciona una persona al azar de este grupo, ¿cuál es la probabilidad de que la edad de la persona sea menor a 20?
Solución
El número de personas cuya edad es menor a 20 está dado por:
120 - 90 = 30
La probabilidad P de que una persona seleccionada al azar del grupo tenga menos de 20 años está dada por:
30 / 120 = 0.25
La longitud de un rectángulo es cuatro veces su ancho. Si el área es 100 m², ¿cuál es la longitud del rectángulo?
Solución
Sea L la longitud y W el ancho del rectángulo. Por lo tanto:
L = 4W
Usamos el área para escribir:
100 = L × W
Sustituimos L por 4W en la ecuación anterior:
100 = 4W × W = 4W²
Resolvemos para W y encontramos L:
4W² = 100
W² = 25, W = 5 y L = 4W = 20 m
Se lanza un dado de seis caras una vez. ¿Cuál es la probabilidad de que el número obtenido sea un número par mayor que 2?
Solución
De los 6 números posibles que pueden salir, 3 son pares: 2, 4 y 6, PERO solo 4 y 6 son mayores que 2. Por lo tanto, la probabilidad de que el número obtenido sea un número par mayor que 2 está dada por:
(número de números pares mayores que 2) / 6 = 2 / 6 = 1 / 3
El punto A tiene las coordenadas (2,2). ¿Cuáles son las coordenadas de su punto imagen si se traslada 2 unidades arriba y 5 unidades a la izquierda, y se refleja en el eje x?
Solución
Una traslación de 2 unidades arriba incrementará la coordenada y en 2 unidades, y una traslación de 5 unidades a la izquierda disminuirá la coordenada x en 5. Por lo tanto, después de estas traslaciones, el punto (2,2) se convierte en:
(2 - 5, 2 + 2) = (-3, 4)
Cuando el punto (-3, 4) se refleja en el eje x, su coordenada y cambia de signo y el punto (-3, 4) se convierte en:
(-3, -4)
La longitud de un rectángulo se incrementa a 2 veces su tamaño original y su ancho se incrementa a 3 veces su tamaño original. Si el área del nuevo rectángulo es igual a 1800 metros cuadrados, ¿cuál es el área del rectángulo original?
Solución
Sean L y W la longitud y el ancho originales del rectángulo, y su área está dada por L × W.
Después del incremento, la longitud se convierte en 2L y el ancho en 3W. El área está entonces dada por (2L) × (3W) y es conocida. Por lo tanto:
(2L) × (3W) = 1800
Resolvemos la ecuación anterior para encontrar L × W:
6 L × W = 1800
L × W = 1800 / 6 = 300 metros cuadrados (área del rectángulo original)
Cada dimensión de un cubo se ha incrementado al doble de su tamaño original. Si el nuevo cubo tiene un volumen de 64,000 centímetros cúbicos, ¿cuál es el área de una cara del cubo original?
Solución
Sea x la longitud de la arista del cubo original. Cuando se incrementa al doble de su tamaño original, se convierte en 2x, lo que da un volumen de:
2x × 2x × 2x = 8x³
El volumen es conocido. Por lo tanto:
8x³ = 64,000
x³ = 8,000, lo que da x = 20
El área de una cara del cubo original (antes del incremento) está dada por x²:
x² = 20² = 400 centímetros cuadrados
La bomba A puede llenar un tanque de agua en 5 horas. La bomba B puede llenar el mismo tanque en 8 horas. ¿Cuánto tiempo tardan las dos bombas trabajando juntas en llenar el tanque? (redondea tu respuesta al minuto más cercano).
Solución
En 1 hora, la bomba A puede llenar 1/5 del tanque y la bomba B puede llenar 1/8 del mismo tanque. Entonces, en 1 hora, las dos bombas trabajando juntas pueden llenar:
1/5 + 1/8 = 13/40 del tanque
Dado que la tasa de las dos bombas trabajando juntas es 13/40, el tiempo t necesario para llenar el tanque por las dos bombas se encuentra resolviendo:
(13/40) t = 1
t = 40 / 13 = 39/13 + 1/13 horas = 3 horas y (1/13)*60 minutos ≈ 3 horas 5 minutos (redondeado al minuto más cercano)
Un tanque de agua, que tiene la forma de un prisma rectangular de base 100 centímetros cuadrados, se está llenando a razón de 1 litro por minuto. Encuentra la tasa a la que aumenta la altura del agua en el tanque. Expresa tu respuesta en centímetros por minuto.
Solución
El volumen de un prisma rectangular está dado por:
área de la base × altura
La tasa a la que se llena el tanque es de 1 litro por minuto, lo que necesitamos convertir:
1 litro = 1 dm³
Pero 1 dm = 10 cm. Por lo tanto:
1 litro = (10 cm)³ = 1000 cm³
La altura h del agua está relacionada con el volumen por:
volumen = área de la base × h
En un minuto, el volumen aumenta en 1 litro o 1000 cm³ y la altura aumenta en:
h = volumen / área de la base = 1000 cm³ / 100 cm² = 10 cm
Dany compró un total de 20 cartas de juego, algunas de las cuales cuestan $0.25 cada una y otras cuestan $0.15 cada una. Si Dany gastó $4.2 para comprar estas cartas, ¿cuántas cartas de cada tipo compró?
Solución
Sea X el número de cartas que cuestan $0.25 cada una e Y el número de cartas que cuestan $0.15 cada una. El número total de cartas es 20. Por lo tanto:
X + Y = 20
Si X es el número de cartas a $0.25, entonces las cartas X cuestan 0.25X.
Si Y es el número de cartas a $0.15, entonces las cartas Y cuestan 0.15Y.
El costo total de las cartas X e Y es $4.2 y también está dado por:
0.25X + 0.15Y = 4.2
Ahora necesitamos resolver el sistema de ecuaciones:
X + Y = 20
0.25X + 0.15Y = 4.2
La primera ecuación da Y = 20 - X. Sustituimos y por 20 - x en la segunda ecuación y resolvemos:
0.25X + 0.15(20 - X) = 4.2
X(0.25 - 0.15) + 3 = 4.2
0.1X = 1.2
X = 12 e Y = 20 - 12 = 8
El tamaño del perímetro del cuadrado ABCD es igual a 100 cm. La longitud del segmento MN es igual a 5 cm y el triángulo MNC es isósceles. Encuentra el área del pentágono ABNMD.
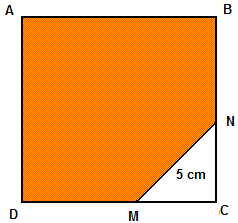
Solución
El área A del pentágono ABNMD puede encontrarse restando el área del triángulo MNC del área total del cuadrado.
A = 25² - (1/2) × MC × NC
Dado que el triángulo MNC es isósceles, la longitud de NC y MC son iguales (MC = NC) y el área anterior puede escribirse como:
A = 25² - (1/2) × MC²
Además, el triángulo MNC es un triángulo rectángulo. Usemos el teorema de Pitágoras para encontrar MC².
MC² + NC² = 5²
Dado que MC = NC, la ecuación anterior puede escribirse como:
2 MC² = 25
MC² = 25 / 2
Ahora sustituimos MC² por 25 / 2 en el área A encontrada anteriormente:
A = 25² - 25 / 4 = 625 - 6.25 = 618.75 centímetros cuadrados
El agua se está bombeando, a una tasa constante, en un tanque de almacenamiento subterráneo que tiene la forma de un prisma rectangular. ¿Cuál de las siguientes gráficas representa mejor los cambios en la altura del agua en el tanque en función del tiempo?

Solución
Cuando se bombea agua a un tanque, la altura del agua aumentará. La gráfica en la parte superior derecha muestra una altura decreciente y la gráfica en la parte inferior derecha muestra una altura constante y, por lo tanto, no puede representar la altura en función del tiempo. La gráfica en la parte superior izquierda no es la gráfica de una función. La única gráfica que puede representar la altura del agua en el tanque que se está llenando es la gráfica en la parte inferior izquierda, que muestra una altura creciente.
Inicialmente, el prisma rectangular de la izquierda estaba lleno de agua. Luego, se vertió agua en el contenedor cilíndrico de la derecha para que las alturas del agua en ambos contenedores fueran iguales. Encuentra la altura h del agua en ambos contenedores (redondea tu respuesta a la décima de cm más cercana).

Solución
El volumen de agua en el prisma rectangular de la izquierda está dado por:
2 × 4 × 10 = 80 cm³
El volumen de agua en el prisma rectangular del medio está dado por:
2 × 4 × h = 8h
El volumen de agua en el cilindro de la derecha está dado por:
π × (1)² × h = π × h, donde π ≈ 3.14
Dado que toda el agua del contenedor de la izquierda se vierte en ambos contenedores de la derecha, entonces:
80 cm³ = 8h + π × h
Resolvemos para encontrar h:
h = 80 / (8 + π)
h ≈ 7.2 cm (redondeado a la décima de cm más cercana)
Peter condujo a una velocidad constante durante 2 horas. Luego se detuvo una hora para hacer algunas compras y descansar, y luego condujo de regreso a casa a una velocidad constante. ¿Qué gráfica representa mejor los cambios en la distancia desde casa mientras Peter conducía?
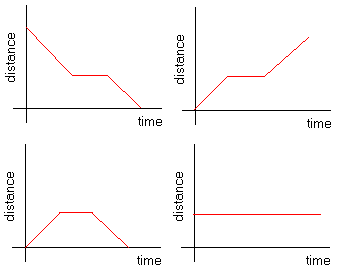
Solución
Cuando Peter se aleja de casa, la distancia desde casa debería aumentar. Solo las gráficas inferior-izquierda y superior-derecha muestran un aumento al inicio (t=0). Mientras hace compras, la distancia se mantiene constante, pero cuando comienza a conducir de regreso, la distancia debe disminuir a medida que se acerca a casa. Por lo tanto, solo la gráfica en la parte inferior-izquierda muestra una disminución de la distancia y representa mejor los cambios en la distancia.
Dos bolas A y B giran a lo largo de una pista circular. La bola A da 2 rotaciones completas en 26 minutos. La bola B da 5 rotaciones completas en 35 minutos. Si comienzan a girar ahora desde el mismo punto, ¿cuándo volverán a estar en el mismo punto de partida?
Solución
Si la bola A da 2 rotaciones en 26 minutos, da 1 rotación en 13 minutos. Si la bola B da 5 rotaciones en 35 minutos, da 1 rotación en 7 minutos.
Las dos bolas comienzan a girar ahora y dan varias rotaciones antes de estar en el MISMO punto de partida. La bola A habría hecho un número ENTERO X de rotaciones y la bola B habría hecho un número ENTERO Y de rotaciones. Además, habrían girado durante el mismo período de tiempo T. Por lo tanto:
T = 13X = 7Y
Por lo tanto, 13X = 7Y
Resolvemos la ecuación anterior para X:
X = 7Y / 13
Queremos el tiempo cuando están PRIMERO en el mismo punto de partida. Por lo tanto, X e Y son los números enteros más pequeños de la ecuación X = 7Y / 13. El valor más pequeño de Y que da X como un número entero es 13. Por lo tanto:
X = 7(13) / 13 = 7
El tiempo T está dado por:
T = 13X = 13 × 7 = 91 minutos = 1 hora y 31 minutos
o T = 7Y = 7 × 13 = 91 minutos = 1 hora y 31 minutos
En cierta universidad, el 40% de los estudiantes de último año toman Física, el 30% toman cálculo y el 10% toman ambas. Si hay 40 estudiantes inscritos en el último año, ¿cuántos estudiantes no toman ni Física ni cálculo?
Joe condujo a la velocidad de 45 millas por hora por cierta distancia. Luego condujo a la velocidad de 55 millas por hora por la misma distancia. ¿Cuál es la velocidad promedio para todo el viaje?
Si el radio de un contenedor cilíndrico se duplica, ¿cómo se debe cambiar la altura del contenedor para que el volumen permanezca igual?
Un cateto de un triángulo rectángulo mide 18 cm y su área es de 108 cm². Encuentra su perímetro.
¿Cuál es la suma de las medidas de los ángulos interiores de un polígono con 53 lados?
Jack es más alto que Sarah pero más bajo que Malika y Tania. Malika es más baja que Tania. Natasha es más baja que Sarah. ¿Quién es el más bajo?
¿Cuál es la altura (uno de los catetos) y la hipotenusa de un triángulo rectángulo isósceles que tiene un área de 800 pies cuadrados?
Encuentra la circunferencia de un círculo inscrito en un cuadrado con un lado de 20 metros.
Dos escuelas diferentes (A y B) tienen el mismo número de alumnos. La proporción de niños en la escuela A y niños en la escuela B es 2:1 y la proporción de niñas en la escuela A y niñas en la escuela B es 4:5. Encuentra la proporción de niños en la escuela A respecto a las niñas en la escuela A.
Un tanque de agua tiene la forma de un prisma rectangular de base 50 cm². Este tanque se está llenando a razón de 12 litros por minuto. Encuentra la tasa a la que aumenta la altura del agua en el tanque; expresa tu respuesta en milímetros por segundo.
Una bomba llena un tanque dos veces más rápido que otra bomba. Si las bombas trabajan juntas, llenan el tanque en 18 minutos. ¿Cuánto tiempo tarda cada bomba trabajando sola en llenar el tanque?