Comprendiendo las Distribuciones Muestrales: Un Ejemplo Concreto
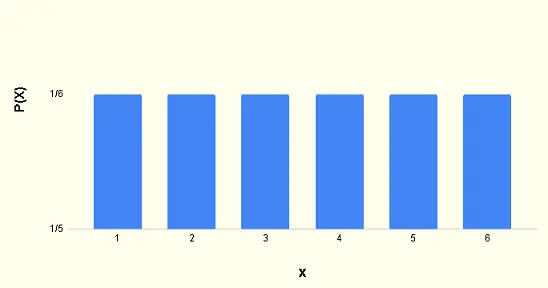
Examinemos una distribución uniforme simple para ilustrar el TLC en acción. Considere una población que consiste en los enteros del 1 al 6 (como un dado justo):
Parámetros de la Población:
Para esta distribución uniforme discreta:
\[ \mu = \frac{1+2+3+4+5+6}{6} = 3.5 \]
\[ \sigma^2 = \frac{\sum_{i=1}^{6} (x_i - \mu)^2}{6} = \frac{(1-3.5)^2 + (2-3.5)^2 + \cdots + (6-3.5)^2}{6} = \frac{35}{12} \approx 2.9167 \]
\[ \sigma = \sqrt{\frac{35}{12}} \approx 1.7078 \]
Distribución Muestral para \( n = 2 \):
Considere todas las muestras posibles de tamaño \( n = 2 \) (con reemplazo):
| 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 |
| 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 |
| 4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,6 |
| 5,1 | 5,2 | 5,3 | 5,4 | 5,5 | 5,6 |
| 6,1 | 6,2 | 6,3 | 6,4 | 6,5 | 6,6 |
Calculemos las medias muestrales \( \bar{X} = \frac{x_1 + x_2}{2} \):
| 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
| 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
| 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 |
| 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 |
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 |
| 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 |
Distribución Muestral de \( \bar{X} \):
| \( \bar{X} \) | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 |
|---|
| \( P(\bar{X}) \) | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
|---|
Parámetros de la Distribución Muestral:
Media de la distribución muestral:
\[ \mu_{\bar{X}} = \sum \bar{X}_i P(\bar{X}_i) = 3.5 = \mu \]
Error estándar (teórico):
\[ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} = \frac{1.7078}{\sqrt{2}} = \sqrt{\frac{35}{24}} \approx 1.2076 \]
Error estándar (a partir de la distribución discreta):
\[ \sigma_{\bar{X}} = \sqrt{\sum (\bar{X}_i - \mu_{\bar{X}})^2 P(\bar{X}_i)} \approx 1.215 \]
Nota: El valor teórico (1.2076) coincide estrechamente con el valor calculado (1.215), demostrando que incluso para un \( n = 2 \) pequeño, la fórmula \( \sigma_{\bar{X}} = \sigma/\sqrt{n} \) proporciona una buena aproximación.
Teorema del Límite Central: Problemas de Práctica y Soluciones Paso a Paso
Ejemplo 1: Probabilidad Básica de Media Muestral
Una población tiene media \( \mu = 20 \) y desviación estándar \( \sigma = 4 \). Se selecciona una muestra aleatoria de 64 observaciones. ¿Cuál es la probabilidad aproximada de que la media muestral sea menor que 19?
Solución
Tamaño de muestra \( n = 64 \ge 30 \), por lo que el TLC aplica:
\[ \mu_{\bar{X}} = \mu = 20 \]
\[ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} = \frac{4}{\sqrt{64}} = 0.5 \]
Calculamos el puntaje Z para \( \bar{X} = 19 \):
\[ Z = \frac{\bar{X} - \mu_{\bar{X}}}{\sigma_{\bar{X}}} = \frac{19 - 20}{0.5} = -2 \]
Usando la distribución normal estándar:
\[ P(\bar{X} < 19) = P(Z < -2) \approx 0.0228 \]
Interpretación: Existe aproximadamente un 2.28% de probabilidad de que una muestra aleatoria de 64 observaciones de esta población tenga una media muestral menor que 19.
Ejemplo 2: Rendimientos de Cartera de Inversión
Un grupo de 251 compañías de inversión tuvo un rendimiento promedio del 4.5% con una desviación estándar del 1.5% durante un período específico. Si se seleccionan aleatoriamente 40 compañías, ¿cuál es la probabilidad de que su rendimiento promedio esté entre el 4% y el 5%?
Solución
El TLC aplica ya que \( n = 40 \ge 30 \):
\[ \mu_{\bar{X}} = 4.5\% \]
\[ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} = \frac{1.5\%}{\sqrt{40}} \approx 0.2372\% \]
Calculamos los puntajes Z para ambos límites:
\[ Z_1 = \frac{4\% - 4.5\%}{0.2372\%} \approx -2.108 \]
\[ Z_2 = \frac{5\% - 4.5\%}{0.2372\%} \approx 2.108 \]
Probabilidad entre los límites:
\[ P(4\% < \bar{X} < 5\%) = P(-2.108 < Z < 2.108) \approx 0.965 \]
Interpretación: Existe aproximadamente un 96.5% de probabilidad de que una muestra aleatoria de 40 compañías tenga un rendimiento promedio entre el 4% y el 5%.
Ejemplo 3: Rendimiento de Fondos Mutuos
Un gran grupo de fondos mutuos tuvo un rendimiento promedio a 5 años del 80% con una desviación estándar del 30%. Si se seleccionan aleatoriamente 50 fondos, ¿cuál es la probabilidad de que su rendimiento promedio supere el 90%?
Solución
El TLC aplica ya que \( n = 50 \ge 30 \):
\[ \mu_{\bar{X}} = 80\% \]
\[ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} = \frac{30\%}{\sqrt{50}} \approx 4.2426\% \]
Calculamos el puntaje Z para \( \bar{X} = 90\% \):
\[ Z = \frac{90\% - 80\%}{4.2426\%} \approx 2.357 \]
Probabilidad de la cola derecha:
\[ P(\bar{X} > 90\%) = P(Z > 2.357) \approx 0.0092 \]
Interpretación: Existe aproximadamente un 0.92% de probabilidad de que una muestra aleatoria de 50 fondos mutuos tenga un rendimiento promedio que supere el 90%.
Ejemplo 4: Control de Calidad en Manufactura
Una fábrica produce herramientas con una longitud promedio de 10 cm y una desviación estándar de 0.3 cm. Si se muestrean aleatoriamente 200 herramientas, ¿cuál es la probabilidad de que la longitud media de la muestra esté dentro de 0.05 cm de la media de la población?
Solución
El TLC aplica ya que \( n = 200 \ge 30 \):
\[ \mu_{\bar{X}} = 10 \text{ cm} \]
\[ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} = \frac{0.3}{\sqrt{200}} \approx 0.0212 \text{ cm} \]
Calculamos los puntajes Z para los límites \( 9.95 \) cm y \( 10.05 \) cm:
\[ Z_1 = \frac{9.95 - 10}{0.0212} \approx -2.358 \]
\[ Z_2 = \frac{10.05 - 10}{0.0212} \approx 2.358 \]
Probabilidad dentro de la tolerancia:
\[ P(9.95 < \bar{X} < 10.05) = P(-2.358 < Z < 2.358) \approx 0.9816 \]
Interpretación: Existe aproximadamente un 98.2% de probabilidad de que una muestra aleatoria de 200 herramientas tenga una longitud media entre 9.95 cm y 10.05 cm.
Ejemplo 5: Problema de Límite de Peso en Aerolínea
Un avión con 200 asientos tiene un límite total de equipaje de 6000 kg. El peso del equipaje de los pasajeros sigue una distribución con media de 28 kg y desviación estándar de 15 kg. ¿Cuál es la probabilidad de que el peso total del equipaje de 200 pasajeros no supere el límite?
Solución
Convertimos a un problema de media muestral. El peso promedio no debe superar:
\[ \text{Promedio máximo} = \frac{6000}{200} = 30 \text{ kg} \]
El TLC aplica ya que \( n = 200 \ge 30 \):
\[ \mu_{\bar{X}} = 28 \text{ kg} \]
\[ \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} = \frac{15}{\sqrt{200}} \approx 1.0607 \text{ kg} \]
Calculamos el puntaje Z para \( \bar{X} = 30 \) kg:
\[ Z = \frac{30 - 28}{1.0607} \approx 1.886 \]
Probabilidad de la cola izquierda:
\[ P(\bar{X} \le 30) = P(Z \le 1.886) \approx 0.9703 \]
Interpretación: Existe aproximadamente un 97.0% de probabilidad de que el peso total del equipaje de 200 pasajeros seleccionados aleatoriamente no supere los 6000 kg.
Nota sobre Corrección por Continuidad:
Cuando se trabaja con datos discretos (como conteos o proporciones) y se usa la aproximación normal, una corrección por continuidad de ±0.5 puede mejorar la precisión. Sin embargo, para medias muestrales de variables continuas (como en la mayoría de los ejemplos anteriores), no se necesita corrección por continuidad.