This is a tutorial on sine function problems. Examples with detailed solutions and explanations are included.

Example - Problem 1

Solution to Problem 1:

1. The maximum value 6 gives the amplitude
   | a | = 6
   
   
2. Solve the above equation for a and select the positive value.
   a = 6
   
   
3. The period may be used to find b using
   period = 2*pi / | b | = pi
   
   
4. Solve for | b |
   | b | = 2
   
   
   
5. Solve for b and select the positive value
   b = 2
   
   
6. Substitute 6 for a in the formula of the function and use f(0) = 6 to write an equation in c.
   6 = 6*sin(b*0 + c)
   
   
7. Which gives sin(c) = 1
   
   
8. Solve for c
   c = pi/2 + k(2*pi) , where k is an integer.
   There is an infinite number of solutions for c.
   
   
9. Select k = 0 since it is the only value that gives c > 0 and less that 2*pi, which gives
   c = pi / 2
   
   
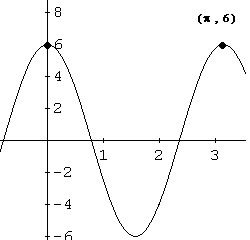
10. Function f is given by f(x) = 6*sin(2x + pi/2)
    
    
    
11. For checking, part of the graph of f is shown below. Check the period and f(0) = 6 and that the maximum value of f(x) is 6.
    
    

Matched Problem 1: Find a, b and c in the sine function f given by

More References and Links