Right Triangle Questions

Multiple choice questions right triangle problems related to trigonometry with answers at the bottom of the page.

Questions with their Answers

Question 1

What is the measure of angle A in the right triangle below?
right triangle question 1

a) 17°
b) 27°
c) 17°
d) 90°

Question 2

What is the value of the side x in the right triangle below?
right triangle question 2

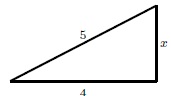
a) 1
b) 9
c) 20
d) 3

Question 3

In a right triangle, the measure of one of the angles is 49° and the hypotenuse has a length of 50 cm. Which of the following is the nearest approximation to the length, in cm, of the leg opposite to this angle?
a) 32.8
b) 57.5
c) 37.7
d) 30.3

Question 4

In the right triangle ABC below, angle A measures 30° and the length of AC is 8 units. Find the length of BC
right triangle question 4

a) 8 / √ 3
b) 4 / √ 3
c) 4
d) 8

Question 5

In the right triangle below, what is sin ??
right triangle question 5

a) 13 / 9
b) 9 / 13
c) 13 √10 / 50
d) 13 / 24

Question 6

Find the length of AC in the right triangle below.
right triangle question 6

a) 9
b) 9 √2
c) 18 √2
d) 18

Question 7

Find the length of the hypotenuse in the right triangle below where x is a real number.
right triangle question 7

a) 5
b) 10
c) 25
d) √ 5

Question 8

Find the area of a square whose diagonal is 40 meters.
a) 80 m²
b) 800 m²
c) 1600 m²
d) 40 m²

Question 9

In the figure below BC is perpendicular to AD, CD = 8, the measure of angle D is 60° and the measure of angle A is 45°. Find the length of AB
right triangle question 9

a) 8 √6
b) 8 √3
c) 8 √2
d) 8

Question 10

What is the length of AB in the figure below.
right triangle question 10

a) 12 √2
b) 12
c) 12 √3
d) 12 √6

Question 11

In the figure below, find cos?.
right triangle question 12

a) 3 / 5
b) 4 / 5
c) 1 / 5
d) 2 / 5

Question 12

In the triangle below, m = ?
right triangle question 13

a) 5
b) 10 √2
c) 20 √2
d) 5 √2