Graphing Square Root Functions

A step by step tutorial on graphing and sketching square root functions . The graph, domain, range and sometimes the simplifications of these functions and other properties are discussed.

Review The domain of function f defined by f(x) = √x is the set of all real positive numbers and zero because the square root of negative numbers are not real numbers (think of √ (- 4), is it real?). In inequality form, the domain of f(x) = √x is written as x ? 0 in interval form the domain is given by [ 0 , + ?) Example 1 Make a table of values of function f given below, graph it and find its range. f( x ) = √x Solution to Example 1 Because the domain of f is the set of all positive real numbers and zero, we might construct a table of values as follows: x 0 1 4 9 16 √x 0 1 2 3 4 The values of x were selected so that the square root of these values are whole numbers which make it easy to plot the points shown in the table. The range of f is given by the interval [0 , +?). Example 2 Find the domain, make a table of values of function f given below, graph it and find its range. f( x ) = √ (x - 3) Solution to Example 2 First find the domain of the square root function given above by stating that the expression under the square root must be positive or equal to zero x - 3 ? 0 Solve the above inequality to obtain the domain of f as the set of all real values such that x ? 3 We now select values of x in the domain to construct a table of values. 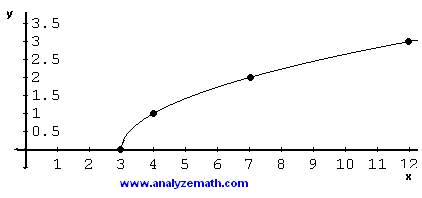x 3 4 7 12 √ (x - 3) 0 1 2 3 The interval [0 , +?) represents the range of f. Example 3 Find the domain, make a table of values of function f given below, graph it and find its range. f( x ) = - √ (- 2x + 4) + 1 Solution to Example 3 The domain of the function given above is found by setting - 2x + 4 ? 0 Solve the above inequality to obtain the domain of f as the set of all real values such that x ? 2 We now select values of x in the domain of f to construct a table of values. These values are selected so that the square root term is a whole number and give points that are easy to plot. x 2 3/2 0 -5/2 -6 - √ (-2 x + 4 ) + 1 1 0 -1 -2 -3 The range of f is given by the interval (-? , 1]. Example 4 Find the domain of function f given below, graph it and find its range. f( x ) = √ (- x 2 + 4) Solution to Example 4 The domain of function given above is found by solving the polynomial inequality - x 2 + 4 ? 0 The solution set of the above inequality is given by the interval [-2 , 2] which is also the domain of the above function. Let us write the given function as an equation as follows y = √ (- x 2 + 4) Square both sides and arrange to obtain. x 2 + y 2 = 2 2 The equation obtained is that of a circle. Hence the graph of f(x) = √ (- x 2 + 4) is the upper half of a circle sinsce √ (- x 2 + 4) is positive. Hence the graph below. 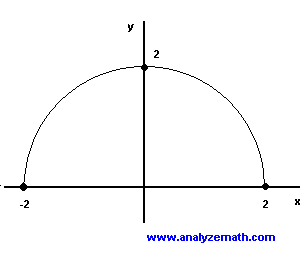The interval [0 , 2] represents the range of f. Example 5 Find the domain, make a table of values of function f given below, graph it and find its range. f( x ) = √ (x 2 - 9) Solution to Example 5 The domain of the function given above is found by solving x 2 - 9 ? 0 Which gives a domain reprsented by (-? , -3] U [3 , + ?) We now select values of x in the domain of f to construct a table of values, noting f(x) = f(-x) hence a symmetry of the graph with respect to the y axis. 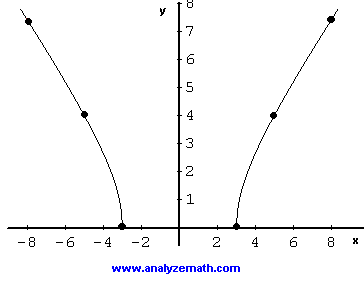x 3 5 8 √ (x 2 - 9) 0 4 7.4 The range of f is given by the interval [0 , + ?). Example 6 Simplify f(x) given below, graph f and find its range. f( x ) = √ (x 2 - 6x + 9) Solution to Example 6 Let us use write the expression under the square root as a square as follows x 2 - 6x + 9 = (x - 3) 2 Hence f( x ) = √ (x 2 - 6x + 9) = √ ( (x - 3) 2 ) = | x - 3 | The given function has been rewitten as an absolute value function. Function f may be written as a piecewise function and graphed as follows. 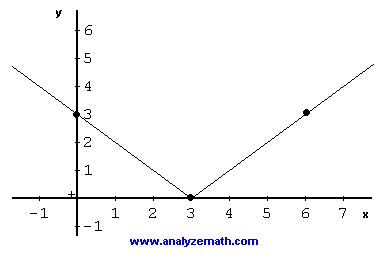The range of f is given by the interval [0 , + ?). Example 7 Graph the radicand (expression under the radical sign), make a table of values of function f given below, graph f and find its range.. f( x ) = √ (x 2 + 4x + 6) Solution to Example 7 Use completing the square to rewtite the expression under the square root as follows x 2 + 4x + 6 = (x + 2) 2 + 2 The expression under the square root is always positive hence the domain of f is the set of all real numbers. Let us first look at the graph of (x + 2) 2 + 2. It is a parabola. We would expect the graph of f to have the same axis of symmetry, the vertical line, x = -2 as the above graph. The table of values may constructed as follows. x -2 0 2 4 √ ( (x + 2) 2 + 2 ) 1.4 2.4 4.2 6.2 The range of f is given by the interval [√2 , + ?). More References and Links to Graphing Graphing Functions