One-To-One Functions

Explore the concept of one-to-one function using examples. This concept is necessary to understand the concept of inverse function definition and its properties and also to solve certain types of equations. Several functions are explored graphically using the horizontal line test. Examples of analytical explanations are, in some cases, provided to support the graphical approach followed here. Some definitions are reviewed so that the explorations can be carried out without difficulties.
More Questions on one to one Functions are included in this website.

One to One Function

Definition of a Function

A function is a rule that produces a correspondence between the elements of two sets: D ( domain ) and R ( range ), such that to each element in D there corresponds one and only one element in R.

Definition of a one-to-one function

A function is a one-to-one if no two different elements in D have the same element in R.
The definition of a one to one function can be written algebraically as follows:
Let x1 and x2 be any elements of D
A function f(x) is one-to-one
if x1 is not equal to x2 then f(x1) is not equal to f(x2)

Using the contrapositive to the above

A function f(x) is one-to-one
if f(x1) = f(x2) then x1 = x2.
This last property is useful in proving that a function is or is not a one to one.
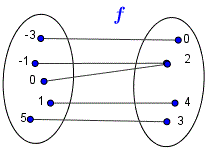
In the Venn diagram below, function f is a one to one since not two inputs have a common output.
the Venn diagram of a one to one function

Figure 1. Venn diagram of a one to one function
In the Venn diagram below, function f is NOT a one to one since the inputs -1 and 0 have the same output.
the Venn diagram of a one to one function

Figure 2. Venn diagram of a function that is not a one to one

Horizontal Line Test

If the graph of a function is known, it is fairly easy to determine if that function is a one to one or not using the horizontal line test.
The graph in figure 3 below is that of a one to one function since for any two different values of the input x (x1 and x2) the outputs f(x1) and f(x2) are different.
the graph of a one to one function

Figure 3. Graph of a one to one function
The graph in figure 4 below is that of a NOT one to one function since for at least two different values of the input x (x1 and x2) the outputs f(x1) and f(x2) are equal.
the graph of function that is not a one to one

Figure 4. Graph of a function that is not a one to one
We can determine graphically if a given function is a one to one by drawing horizontal lines. If none of these horizontal lines cuts the graph of the function in two points or more the the function is a one to one; otherwise it is not a one to one.

Examples of One to One Functions

Example 1

Show algebraically that all linear functions of the form f(x) = a x + b , with a ? 0, are one to one functions.
Solution
We use the contrapositive that states that function f is a one to one function if the following is true:
if f(x1) = f(x2) then x1 = x2
We start with
f(x1) = f(x2)
which gives
a x1 + b = a x2 + b
Simplify to obtain
a ( x1 - x2) = 0
Since a ? 0 the only condition for the above to be satisfied is to have
x1 - x2 = 0
which gives
x1 = x2
We have shown that f(x1) = f(x2) leads to x1 = x2 and according to the contrapositive above, all linear function of the form f(x) = a x + b , with a ? 0, are one to one functions.

Example 2

Show analytically and graphically that the function f(x) = - x2 + 3 is not a one to one functions.
Solution
We use the contrapositive that states that function f is a one to one function if the following is true:
if f(x1) = f(x2) then x1 = x2
We start with
f(x1) = f(x2)
which gives
- x12 + 3 = - x22 + 3
Simplify to obtain
- ( x12 - x22) = 0
Factor - ( x1 - x2)( x1 + x2) = 0 which gives
x1 - x2 = 0 or x1 + x2 = 0
which gives
x1 = x2 or x1 = - x2
Since the above test does not strictly conclude that x1 = x2 the function is not a one to one.
Below is shown the graph of the given function and two horizontal lines are drawn: the x axis and the line y = - 2 (broken line) that shows clearly that there are two points of intersections and therefore the function is not a one to one.
the graph of a quadratic function, not a one to one

Figure 5. Graph of a quadratic function and is not a one to one

Example 3

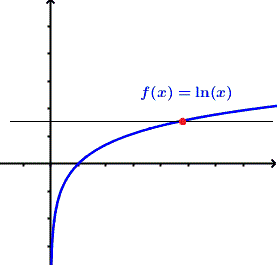
Show graphically that each of the following functions is a one to one function.
1) f(x) = ln(x)
2) g(x) = ex
3) h(x) = x3
Solution
The graph of each of the above functions is shown below with a horizontal line that shows one point of intersection only and therefore all the three functions are one to one functions.
1)
the graph of ln(x) function with a horizontal line that shows that it is not a one to one

Figure 6. Graph of ln(x) with a horizontal line that shows that it is not a one to one
2)
the graph of exponential function with a horizontal line that shows that it is not a one to one

Figure 7. Graph of natural exponential ex function with a horizontal line that shows that it is not a one to one
3)
the graph of cubic with a horizontal line that shows that it is not a one to one

Figure 7. Graph of cubic function with a horizontal line that shows that it is not a one to one

How are One to One Functions Used?

One to one functions are used in

1) Inverse
One to one functions have inverse functions that are also one to one functions.
2) Solving certain types of equations
Examples 1
To solve equations with logarithms such as
ln(2x + 3) = ln(4x - 2)
we deduce the algebraic equation because the ln function is a one to one.
2x + 3 = 4x - 2
Examples 2
To solve equations with exponentials such as
e- x + 2 = e3 x - 8
we deduce the algebraic equation because the ex function is a one to one.
- x + 2 = 3 x - 8

More Questions on one to one Functions are included in this website.

More References and links on or related to one to one functions

Questions on one to one Functions
inverse function definition
properties