Special Right Triangles

\( \qquad h^2 = a^2 + a^2 \)
Simplify and solve foe \( h \)
\( \qquad h^2 = 2 a^2 \)
\( \qquad h = a \sqrt 2 \)
Let us now use the above triangle, apply the six trigonometric ratios to find all six trigonometric ratios of an angle of \( 45^{\circ} \).

\( \qquad \sin 45^{\circ} = \dfrac{\text{Opposite Side}}{\text{Hypotenuse}} = \dfrac{a}{h} = \dfrac{a}{a \sqrt 2} = \dfrac{1}{ \sqrt 2} = \dfrac{\sqrt 2}{2} \)

\( \qquad \cos 45^{\circ} = \dfrac{\text{Adjacent Side}}{\text{Hypotenuse}} = \dfrac{a}{h} = \dfrac{a}{a \sqrt 2} = \dfrac{1}{ \sqrt 2} = \dfrac{\sqrt 2}{2} \)

\( \qquad \tan 45^{\circ} = \dfrac{\text{Opposite Side}}{\text{Adjacent Side}} = \dfrac{a}{a} = 1 \)

\( \qquad \csc 45^{\circ} = \dfrac{1}{\sin 45^{\circ}} = \dfrac{2}{\sqrt 2} =\sqrt 2 \)

\( \qquad \sec 45^{\circ} = \dfrac{1}{\cos 45^{\circ}} = \dfrac{2}{\sqrt 2} = \sqrt 2 \)

\( \qquad \cot 45^{\circ} = \dfrac{1}{\tan 45^{\circ}} = \dfrac{1}{1} = 1 \)

We start with an equilateral triangle with side \( a \) as shown in figure 2 below. Then draw a perpendicular from one of the vertices of the triangle to the opposite base. This perpendicular bisects the angle into two equal angles of \( 30^{\circ} \) and the opposite side into two equal segments of length \( \dfrac{a}{2} \) as shown in figure 3 below.

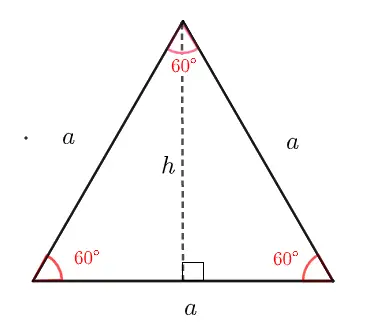Figure 2

Figure 3

This special right triangle 30-60-90 in figure 3 helps us find the six trigonometric ratios of angles \( 30^{\circ} \) and \( 60^{\circ} \).

We first use the Pythagorean theorem to find the side \( h\).

\( \qquad a^2 = h^2 + \left(\dfrac{a}{2}\right)^2 \)

Solve for \( h^2 \).
\( \qquad h^2 = a^2 - \dfrac{a^2}{4} = 3 \dfrac{a^2}{4} \)
Take the square root of both sides to solve for \( h \).
\( \qquad h = \dfrac{a \sqrt 3}{2} \)

We now use the above triangle to find all six trigonometric ratios of \( 30^{\circ} \).

\( \qquad \sin 30^{\circ} = \dfrac{\text{Opposite Side}}{\text{Hypotenuse}} = \dfrac{\dfrac{a}{2}}{a} = \dfrac{1}{2} \)

\( \qquad \cos 30^{\circ} = \dfrac{\text{Adjacent Side}}{\text{Hypotenuse}} = \dfrac{h}{a} = \dfrac{\dfrac{a \sqrt 3}{2}}{a} = \dfrac{\sqrt 3}{2} \)

\( \qquad \tan 30^{\circ} = \dfrac{\text{Opposite Side}}{\text{Adjacent Side}} = \dfrac{\dfrac{a}{2}}{h} = \dfrac{\dfrac{a}{2}}{\dfrac{a \sqrt 3}{2}} = \dfrac{1}{\sqrt 3} \)

\( \qquad \csc 30^{\circ} = \dfrac{1}{\sin 30^{\circ}} = \dfrac{1}{1/2} = 2 \)

\( \qquad \sec 30^{\circ} = \dfrac{1}{\cos 30^{\circ}} = \dfrac{2}{\sqrt 3} \)

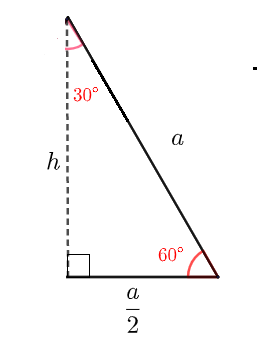\( \qquad \cot 30^{\circ} = \dfrac{ 1 }{\tan 30^{\circ} } = \sqrt 3 \)

We now use the same triangle in figure 3 to find all six trigonometric ratios of \( 60^{\circ} \).
\( \qquad \sin 60^{\circ} = \dfrac{\text{Opposite Side}}{\text{Hypotenuse}} = \dfrac{h}{a} = \dfrac{\dfrac{a \sqrt 3}{2}}{a} = \dfrac{\sqrt 3}{2} \)

\( \qquad \cos 60^{\circ} = \dfrac{\text{Adjacent Side}}{\text{Hypotenuse}} = \dfrac{a/2}{a} = \dfrac{1}{2} \)

\( \qquad \tan 60^{\circ} = \dfrac{\text{Opposite Side}}{\text{Adjacent Side}} = \dfrac{h}{a/2} = \dfrac{\dfrac{a \sqrt 3}{2}}{a/2} = \sqrt 3 \)

\( \qquad \csc 60^{\circ} = \dfrac{1}{\sin 60^{\circ}} = \dfrac{1}{\dfrac{\sqrt 3}{2}} = \dfrac{2}{\sqrt 3} \)

\( \qquad \sec 60^{\circ} = \dfrac{1}{\cos 60^{\circ}} = \dfrac{1}{1/2} = 2\)

\( \qquad \cot 60^{\circ} = \dfrac{ 1 }{\tan 60^{\circ} } = \dfrac{1}{\sqrt 3} \)

Table of the Six Trigonomeotric Functions for Special Angles

Here we group all values of the six trigonometric function in a table.
NOTE that the letter \( U \) used in the table mean undefined.

\( {\theta \;\;\; \text{( in Degrees )} }\)	\( { 0^{\circ} } \)	\( { 30^{\circ} } \)	\( { 45^{\circ} } \)	\( { 60^{\circ} } \)	\( { 90^{\circ} } \)
\( {\theta \;\;\; \text{( in Radians )} }\)	\( { 0 } \)	\( { \dfrac{\pi}{6} } \)	\( { \dfrac{\pi}{4} } \)	\( { \dfrac{\pi}{3} } \)	\( { \dfrac{\pi}{2} } \)
\( {\sin \theta}\)	\( 0 \)	\( \dfrac{1}{2} \)	\( \dfrac{\sqrt 2}{2} \)	\( \dfrac{\sqrt 3}{2} \)	\( 1 \)
\( {\cos \theta} \)	\( 1 \)	\( \dfrac{\sqrt 3}{2} \)	\( \dfrac{\sqrt 2}{2} \)	\( \dfrac{1}{2} \)	\( 0 \)
\( { \tan \theta } \)	\( 0 \)	\( \dfrac{1}{\sqrt 3} \)	\( 1 \)	\( \sqrt 3 \)	\( \text{U}\)
\( {\csc \theta}\)	\( \text{U}\)	\( 2 \)	\( \sqrt 2 \)	\( \dfrac{2}{\sqrt 3} \)	\( 1 \)
\( {\sec \theta} \)	\( 1 \)	\( \dfrac{2}{\sqrt 3} \)	\( \sqrt 2 \)	\( 2 \)	\( \text{U}\)
\( { \cot \theta } \)	\( \text{U}\)	\( \sqrt 3 \)	\( 1 \)	\( \dfrac{1}{\sqrt 3} \)	\( 0 \)