Solve Trigonometry Problems Using Trigonometric Ratios

This page presents a collection of right-triangle trigonometry problems solved using the six trigonometric ratios. Each problem includes clear reasoning and step-by-step solutions.

Definition of Trigonometric Ratios

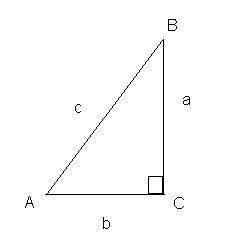
Right triangle showing trigonometric ratios

In a right triangle, the six trigonometric ratios are defined as follows:

  1. Sine: \[ \sin(A) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{a}{c} \]
  2. Cosine: \[ \cos(A) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{b}{c} \]
  3. Tangent: \[ \tan(A) = \frac{\text{opposite}}{\text{adjacent}} = \frac{a}{b} \]
  4. Secant: \[ \sec(A) = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{c}{b} \]
  5. Cosecant: \[ \csc(A) = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{c}{a} \]
  6. Cotangent: \[ \cot(A) = \frac{\text{adjacent}}{\text{opposite}} = \frac{b}{a} \]

Worked Problems

Problem 1

Given the right triangle below, find \(\sin A\), \(\cos A\), \(\tan A\), \(\sec A\), \(\csc A\), and \(\cot A\).

Right triangle for Problem 1

Solution

First, find the hypotenuse using Pythagoras' theorem:

\[ c^2 = 8^2 + 6^2 = 100 \quad \Rightarrow \quad c^2 = 100 \quad \Rightarrow c = \sqrt{100} = 10 \]

Now apply the trigonometric ratios:

\[ \sin A = \frac{8}{10} = \frac{4}{5} \] \[ \cos A = \frac{6}{10} = \frac{3}{5} \] \[ \tan A = \frac{8}{6} = \frac{4}{3} \] \[ \sec A = \frac{10}{6} = \frac{5}{3} \] \[ \csc A = \frac{10}{8} = \frac{5}{4} \] \[ \cot A = \frac{6}{8} = \frac{3}{4} \]

Problem 2

Find the length of the hypotenuse \(c\).

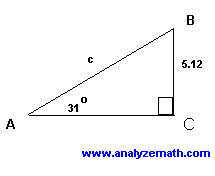
Right triangle for Problem 2

Solution

Using the sine ratio:

\[ \sin 31^\circ = \frac{5.12}{c} \]

Solving for \(c\):

\[ c = \frac{5.12}{\sin 31^\circ} \approx 9.94 \]

Problem 3

If \(x\) is an acute angle and \(\sin x = \frac{3}{7}\), find the exact values of \(\cos x\) and \(\cot x\).

Solution

Start with: \(\sin x = \frac{\text{Opposite}}{\text{Hypotenues}} = \dfrac{3}{7}\)

Let opposite \(= 3\) and hypotenuse \(= 7\). Find the adjacent side:

Pythora's theorem gives: \[ 7^2 = a^2 + 3^2 \Rightarrow a = \sqrt{40} = 2\sqrt{10} \] \[ \cos x = \frac{2\sqrt{10}}{7} \quad\quad \cot x = \frac{2\sqrt{10}}{3} \]

Problem 4

Find the exact values of \(x\) and \(y\).

Right triangle for Problem 4

Solution

\[ \sin 30^\circ = \frac{x}{10} \Rightarrow x = 10 \sin 30^\circ = 10 \cdot \dfrac{1}{2} = 5 \] \[ 10^2 = 5^2 + y^2 \Rightarrow y = \sqrt{75} = 5\sqrt{3} \]

Problem 5

If \(\tan x = 5\), find the exact values of \(\sin x\) and \(\cos x\).

Solution

Start with: \(\tan x = \frac{\text{Opposite}}{\text{Adjacent}} = \dfrac{5}{1}\)

Let opposite \(= 5\) and adjacent \(= 1\).

\[ \text{hypotenuse} = \sqrt{1^2 + 5^2} = \sqrt{26} \] \[ \sin x = \frac{5}{\sqrt{26}} \quad\quad \cos x = \frac{1}{\sqrt{26}} \]

Problem 6 (Challenge)

An acute angle \( \theta \) of a right triangle satisfies \[ \sin \theta + \cos \theta = \frac{7}{5}. \] Find the exact values of \( \sin \theta \) and \( \cos \theta \).

Solution

Square both sides of the given equation \[ (\sin \theta + \cos \theta )^2 = \left(\frac{7}{5} \right)^2. \]

Use the identity \[ (\sin \theta + \cos \theta)^2 = \sin^2 \theta + \cos^2 \theta + 2\sin \theta \cos \theta. \]

and the Pythagorean identity \( \sin^2 \theta + \cos^2 \theta = 1 \), we obtain

\[ \left(\frac{7}{5}\right)^2 = 1 + 2\sin \theta \cos \theta \] \[ \frac{49}{25} = 1 + 2\sin \theta \cos \theta \] \[ 2\sin \theta \cos \theta = \frac{24}{25} \] \[ \sin \theta \cos \theta = \frac{12}{25} \]

Now we have the system:

\[ \sin \theta + \cos \theta = \frac{7}{5} \] \[ \sin \theta \cos \theta = \frac{12}{25} \]

These are the sum and product of two positive numbers. Let \( x = \sin \theta \) and \( y = \cos \theta \).

\[ x+ y = \frac{7}{5} \quad (1) \] \[ x \cdot y = \frac{12}{25} \quad (2) \] Solve equation (1) for \( y \) \[ y = \frac{7}{5} - x \] Substitute in equation (2) \[ x \cdot (\frac{7}{5} - x ) = \frac{12}{25} \quad (2) \] Rearrange to write \[ x^2 - \frac{7}{5}x + \frac{12}{25} = 0 \]

Multiply through by 25:

\[ 25x^2 - 35x + 12 = 0 \]

Factor:

\[ (5x - 3)(5x - 4) = 0 \] \[ x = \frac{3}{5} \quad \text{or} \quad x = \frac{4}{5} \]

Since \( \theta \) is acute, both sine and cosine are positive and using the equation \( x \cdot y = \frac{12}{25} \), we obtain:

\[ \boxed{ x = \sin \theta = \frac{3}{5}, \quad y = \cos \theta = \frac{4}{5}} \] or (depending on the orientation of the triangle) \[ \boxed{ x = \sin \theta = \frac{4}{5}, \quad y = \cos \theta = \frac{3}{5}} \]

More Trigonometry Resources