Geometry Problems with Solutions and Answers

Solve the linear equation \( x - y = 1 \) for \( x \):

\( x = 1 + y \)

Substitute into the standard equation of the given circle :

\[ (1 + y)^2 + 2(1 + y) + y^2 + 4y = -1 \]

Expand and simplify the expression. Combine like terms and rewrite the resulting quadratic equation in standard form:

\[ 2y^2 + 8y + 4 = 0 \]

Solve the quadratic equation to get the values of \( y \):

\[ y = -2 \pm \sqrt{2} \]

Use the substitution \( x = 1 + y \) to find the corresponding \( x \)-values.

Therefore, the points of intersection between the line and the circle are:

\[ (-1 + \sqrt{2},\ -2 + \sqrt{2}) \quad \text{and} \quad (-1 - \sqrt{2},\ -2 - \sqrt{2}) \]

To find the area of the triangle formed by the lines \( y = x \) and \( y = -2x + 3 \), first graph both lines.

Solve the system of equations to find the intersection point:

\[ y = x \quad \text{and} \quad \; y = -2x + 3 \]

Solving, we find the intersection point is \( (1,\ 1) \). The height of the triangle is 1 (the y-coordinate).

The x-intercept of \( y = -2x + 3 \) is found by setting \( y = 0 \): \[ 0 = -2x + 3 \Rightarrow x = \dfrac{3}{2} \]

The base of the triangle is \( \dfrac{3}{2} \). So, the area is:

\[ \text{Area} = \dfrac{1}{2} \times \text{base} \times \text{height} = \dfrac{1}{2} \times \dfrac{3}{2} \times 1 = \dfrac{3}{4} \]

The sine formula for the area of a triangle using two sides and the included angle can be written as:

\[ 18 = \dfrac{1}{2} \times 5 \times 10 \times \sin(A) \]

Solving for \( \sin(A) \), we get:

\[ \sin(A) = \dfrac{18}{25} \]

We now use the cosine law to find the length \( x \) of the third side opposite angle \( A \):

\[ x^2 = 5^2 + 10^2 - 2 \times 5 \times 10 \times \cos(A) \]

Since \( \cos(A) = \sqrt{1 - \sin^2(A)} \), we substitute:

\[ \cos(A) = \sqrt{1 - \left(\dfrac{18}{25}\right)^2} \]

Substitute \( \cos(A) \) into the cosine law expression and solve for \( x \):

\[ x \approx 7.46 \quad \text{(rounded to 3 significant digits)} \]

The area of triangle BOC is 15 and is given by \[ \text{Area}_{\triangle BOC} = \dfrac{1}{2} \cdot BO \cdot OC \cdot \sin(\angle BOC) \]

The area of triangle AOD is given by \[ \text{Area}_{\triangle AOD} = \dfrac{1}{2} \cdot AO \cdot OD \cdot \sin(\angle AOD) \]

Note that angles \( \angle BOC \) and \( \angle AOD \) are equal.

By the theorem of the intersecting chords, we have: \[ AO \cdot OC = BO \cdot OD \]

This can be written as: \[ \dfrac{AO}{BO} = \dfrac{OD}{OC} = \dfrac{10}{5} = 2 \]

The ratios \( \dfrac{AO}{BO} \) and \( \dfrac{OD}{OC} \) are both equal to 2, hence their product is: \[ \dfrac{AO \cdot OD}{BO \cdot OC} = 4 \]

Which gives: \[ AO \cdot OD = 4 \cdot (BO \cdot OC) \]

Therefore, the area of triangle AOD is 4 times the area of triangle BOC: \[ \text{Area}_{\triangle AOD} = 4 \cdot 15 = 60 \]

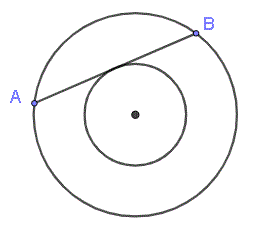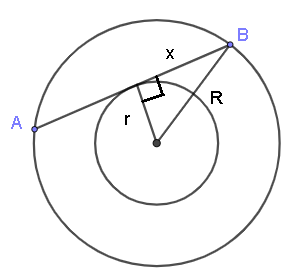
If we draw a radius in the small circle to the point of tangency, it will be at right angle with the chord (see figure below). If \( x \) is half the length of \( AB \), \( r \) is the radius of the small circle, and \( R \) is the radius of the large circle, then by the Pythagorean Theorem, we have:

\[ r^2 + x^2 = R^2 \] \[ 6^2 + x^2 = 10^2 \]

Solve for \( x \): \( x = 8 \)

Length of \( AB = 2x = 16 \)

Use cosine law in triangle ABE:

\[ 13^2 = 20^2 + 9^2 - 2(20)(9)\cos(T) \tag{I} \]

Use cosine law in triangle ACB:

\[ x^2 = 20^2 + 9^2 - 2(20)(9)\cos(90^\circ - T) \]

Note that \( \cos(90^\circ - T) = \sin(T) \) and rewrite the second equation as:

\[ x^2 = 20^2 + 9^2 - 2(20)(9)\sin(T) \tag{III} \]

Solve equation (I) for \( \cos(T) \):

\[ \cos(T) = \dfrac{13}{15} \]

Use the trigonometric identity \( \sin(T) = \sqrt{1 - \cos^2(T)} \) to find:

\[ \sin(T) = \dfrac{2\sqrt{14}}{15} \]

Substitute \( \sin(T) = \dfrac{2\sqrt{14}}{15} \) into equation (III) and solve for \( x \):

\[ x = \sqrt{481 - 48\sqrt{14}} \approx 17.4 \]

(Approximated to 3 significant digits.)

a) Volume of the Composite Solid 1. Volume of the cylinder: \[ V_{\text{cylinder}} = \pi r^2 h = \pi (5)^2 (12) = \pi (25)(12) = 300\pi \, \text{cm}^3 \] 2. Volume of the hemisphere: \[ V_{\text{hemisphere}} = \frac{1}{2} \left( \frac{4}{3} \pi r^3 \right) = \frac{2}{3} \pi (5)^3 = \frac{2}{3} \pi (125) = \frac{250}{3} \pi \, \text{cm}^3 \] 3. Total volume: \[ V_{\text{total}} = V_{\text{cylinder}} + V_{\text{hemisphere}} = 300\pi + \frac{250}{3}\pi = \left( \frac{900 + 250}{3} \right)\pi = \frac{1150}{3} \pi \, \text{cm}^3 \] b) Mass of the Object \[ \text{Mass} = \text{Density} \times \text{Volume} = 7.8 \times \frac{1150}{3} \pi \] Approximating using \(\pi \approx 3.1416 \): \[ \text{Mass} \approx 7.8 \times \frac{1150}{3} \times 3.1416 \approx 9396.66 \, \text{g} \]

a) Area of the Garden 1. Area of the rectangle: \[ A_{\text{rect}} = \text{length} \times \text{width} = 12 \times 8 = 96 \, \text{m}^2 \] 2. **Area of the semicircle (with radius $r = 4$ meters): \[ A_{\text{semi}} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (4)^2 = \frac{1}{2} \pi (16) = 8\pi \, \text{m}^2 \] 3. **Total area: \[ A_{\text{total}} = A_{\text{rect}} + A_{\text{semi}} = 96 + 8\pi \, \text{m}^2 \] Using $\pi \approx 3.1416$: \[ A_{\text{total}} \approx 96 + 8(3.1416) = 96 + 25.13 = \boxed{121.13 \, \text{m}^2} \] b) Perimeter of the Garden Note: We exclude the shared edge between the semicircle and rectangle. 1. Three sides of the rectangle (excluding the 8 m side): \[ P_{\text{rect}} = 12 + 8 + 12 = 32 \, \text{m} \] 2. Curved part of the semicircle: \[ P_{\text{semi}} = \frac{1}{2} (2\pi r) = \pi r = \pi \cdot 4 = 4\pi \, \text{m} \] 3. Total perimeter: \[ P_{\text{total}} = 32 + 4\pi \approx 32 + 12.566 = \boxed{44.57 \, \text{m}} \]