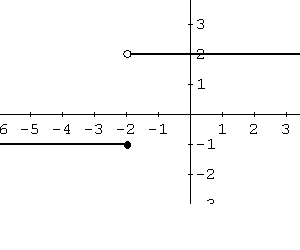Definizione delle funzioni a tratti
Una funzione a tratti � di solito definito da pi� di una formula: un fomula per ogni intervallo.
Esempio 1:
f (x) = - x se x <= 2
� � � �� = x se x> 2
Ci� che il sopra detto � che se x � minore o uguale a 2, la formula per la funzione f (x) = x-e se x � maggiore di 2, la formula � f (x) = x. E 'anche importante notare che il dominio della funzione f definita sopra � l'insieme di tutti i numeri reali in quanto f � definita in tutto il mondo per tutti i numeri reali.
Esempio 2:
f (x) = 2 se x > -3
� � � �� = -5, se x <-3
La funzione di cui sopra � costante e pari a 2 se x � maggiore di -3. funzione f � costante e pari a -5, se x � minore di -3. Si pu� dire che la funzione f � costante a tratti. Il dominio di F sopra riportato � l'insieme di tutti i numeri reali tranne -3: se x = -3 funzione f non � definita.
Esempio 3:
Funzioni che comportano valore assoluto sono anche un buon esempio di funzioni a tratti.
f (x) = | x |
Utilizzando la definizione del valore assoluto, la funzione f di cui sopra pu� essere scritta
f (x) = x se x> = 0
� � � �� = -x se x <0
Il dominio della funzione di cui sopra � l'insieme di tutti i numeri reali.
Esempio 4:
Un altro esempio che coinvolgono vaule assoluto.
f (x) = | x + 6 |
La funzione di cui sopra pu� essere scritta come
f (x) = x + 6 se x> = -6
� � � �� = - (x + 6) se x <-6
La funzione di cui sopra � definita per tutti i numeri reali.
Esempio 5:
Un altro esempio che coinvolgono pi� di due intervalli.
f (x) = x 2 - 3 se x <= -10
� � � �� = - 2x + 1 se -10 <x <= -2
� � � �� = - x 3 se 2 <x <4
� � � ��= Ln x se x> 4
La funzione di cui sopra � definita per tutti i numeri reali tranne che per i valori di x nell'intervallo (-2, 2] e x = 4.
Esempio 6: f � una funzione definita da
f (x) = -1 se x <= -2
� � � �� = 2 se x> -2
Trovare il dominio e la gamma della funzione f e graficamente.
Soluzione Esempio 6:
Funzione f � definita per tutti i valori reali di x. Il dominio di f � l'insieme di tutti i numeri reali. Saremo grafico dal considerare il valore della funzione in ogni intervallo.
Nell'intervallo (- inf, -2] il grafico di f � una linea orizzontale y = f (x) = -1 (vedi la formula di questo intervallo di cui sopra). Anche questo intervallo � chiuso in x = -2 e quindi il grafico deve mostrare questo: vedere la sezione "chiuso" punto sul grafico in x = -2.
Nell'intervallo (-2, + inf), il grafico � una retta orizzontale = f (x) = 2 (vedi la formula di questo intervallo di cui sopra). L'intervallo (-2, + inf) � aperto in x = -2 e il grafico illustra questo con un punto "aperto". Funzione f pu� assumere solo due valori: -1 e 2. La gamma � dato da (-1, 2)
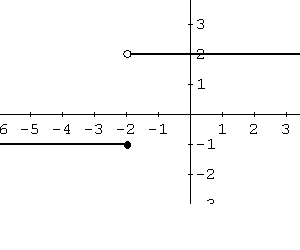


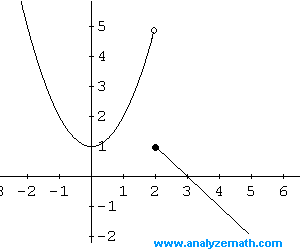
Esempio 7: f � una funzione definita da
f (x) = x 2 + 1 se x <2
� � � �� = - x + 3 se x> = 2
Trovare il dominio e la gamma della funzione f e graficamente.
Soluzione Esempio 7:
Il dominio di f � l'insieme di tutti i numeri reali in quanto la funzione f � definita per tutti i valori reali di x.
Nell'intervallo (- inf, 2) il grafico di f � una parabola spostata verso l'alto 1 unit�. Anche questo intervallo � aperto in x = 2 e quindi il grafico mostra un punto di "aprire" sul grafico in x = 2.
Nell'intervallo [2, + inf), il grafico � una linea con una intercetta x a (3, 0) e passante per il punto (2, 1). L'intervallo [2, + inf) � chiuso in x = 2 e il grafico mostra un "punto di chiusura". Dal grafico, si pu� osservare che la funzione f pu� assumere tutti i valori reali. La gamma � data da (- inf, + inf).


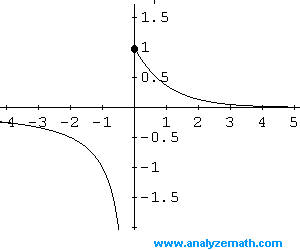
Esempio 8: f � una funzione definita da
f (x) = 1 / x se x <0
� � � �� = e-x se x> = 0
Trovare il dominio e la gamma della funzione f e graficamente.
Soluzione Esempio 8:
Il dominio di f � l'insieme di tutti i numeri reali in quanto la funzione f � definita per tutti i valori reali di x.
Nell'intervallo (- inf, 0) il grafico di f � una iperbole con asintoto verticale in x = 0.
Nell'intervallo [0, + inf), il grafico � un esponenziale decrescente e passa attraverso il punto (0, 1). L'intervallo [0, + inf) � chiuso in x = 0 e il grafico mostra un "punto di chiusura".
Come x diventa molto piccola, 1 / x si avvicina allo zero. Come x diventa molto grande, e-x si avvicina anche allo zero. Quindi la retta y = 0 � un asintoto orizzontale per il grafico di f.
Dal grafico di f di seguito riportate, si pu� osservare che la funzione f pu� assumere tutti i valori reali su (- inf, 0) U (0, 1], che � la gamma della funzione f.


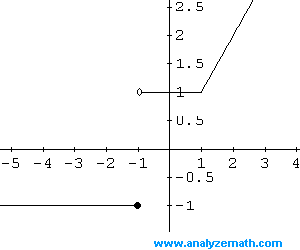
Esempio 9: f � una funzione definita da
f (x) = -1 se x <= -1
� � � �� = 1 se -1 <x <= 1
� � � �� = x se x> 1
Trovare il dominio e la gamma della funzione f e graficamente.
Soluzione Esempio 9:
Il dominio di f � l'insieme di tutti i numeri reali.
Nell'intervallo (- inf, -1], il grafico di f � una linea orizzontale y = f (x) = -1. Chiuso punto x = -1 dal intervallo chiuso in x = -1.
Nell'intervallo (-1, 1], il grafico � una linea orizzontale. Ci dovrebbe un punto chiuso x = 1 ma leggete qui di seguito.
Durante l'intervallo (1, + inf), il grafico � la retta y = x. Si dovrebbe aprire un punto in x = 1 in quanto l'intervallo � aperto in x = 1. Ma un punto di chiusura (vedi sopra) e un punto in sospeso nella stessa posizione diventa un "normale" punto.
Dal grafico di f di seguito riportate, si pu� osservare che la funzione f pu� assumere tutti i valori reali su (-1) U [1, + inf), che � l'intervallo della funzione f.
Pi� riferimenti e link a grafica.
Graphing Funzioni
|