Reglas de Integrales con Ejemplos

Se presenta un tutorial, con ejemplos y soluciones detalladas, sobre el uso de las reglas de las integrales indefinidas en cálculo. También se incluye un conjunto de preguntas con soluciones.

En lo que sigue, C es una constante de integración y puede tomar cualquier valor.

1 - Integral de una función potencia: \( f(x) = x^n \)

Ejemplo: Evaluar la integral \[ \int x^5 dx \]
Solución: \[ \int x^5 dx = \dfrac{x^{5 + 1}}{ 5 + 1} + c = \dfrac{x^6}{6} + c \]

2 - Integral de una función \( f \) multiplicada por una constante \( k \): \( k f(x) \)

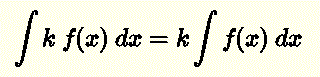
Ejemplo: Evaluar la integral \[ \int 5 \sin \; x dx \] Solución:
De acuerdo con la regla anterior
\( \displaystyle \int 5 \sin (x) dx = 5 \int \sin(x) dx \)
\( \displaystyle \int \sin(x) dx \)   se obtiene de la 2.1 en la tabla de fórmulas de integrales, por lo tanto
Entonces
\( \displaystyle \int 5 \sin(x) dx = - 5 \cos x + C \)

3 - Integral de la Suma de Funciones.

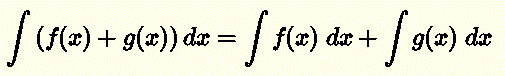
Ejemplo: Evaluar la integral \[ \int (x + e^x) dx \]
Solución:
De acuerdo con la propiedad anterior
\( \displaystyle \int (x + e^x) dx = \int x \; dx + \int e^x \; dx \)
\( \displaystyle \int x \; dx \) se obtiene de la 1.3 y \( \displaystyle \int e^x \; dx \) de la 4.1 en la tabla de fórmulas de integrales, por lo tanto
\[ \int (x + e^x) \; dx = \dfrac{x^2}{2}x + e^x + c \]

4 - Integral de la Diferencia de Funciones.

Ejemplo: Evaluar la integral \[ \int (2 - 1/x) \; dx \]
Solución:
De acuerdo con la propiedad anterior
\( \displaystyle \int (2 - 1/x) dx = \int 2 \; dx - \int (1/x) \; dx \)
\( \int 2 \; dx \) se obtiene de la 1.2 y \( \int (1/x) \; dx \) de la 1.4 en la tabla de fórmulas de integrales, por lo tanto
\[ \int (2 - 1/x) \; dx = 2x - \ln |x| + c \]

5 - Integración por Sustitución.

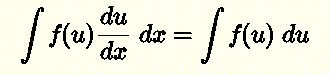
Ejemplo: Evaluar la integral \[ \int (x^2 - 1)^{20} 2x \; dx \]
Solución:
Sea \( u = x^2 - 1\), entonces \( du/dx = 2x \) y la integral dada puede escribirse como
\( \displaystyle \int(x^2 - 1)^{20} \; 2x \; dx = \int u^{20} (du/dx) dx = \int u^{20} du \)
lo cual evalúa a
\( = \dfrac{u^{21}}{21} + c \)
Sustituyendo de vuelta
\( = \dfrac{(x^2 - 1)^{21}}{21} + c \)

6 - Integración por Partes.

Ejemplo: Evaluar la integral \[ \int \; x \; \cos x \; dx \]
Solución:
Sea \( f(x) = x \) y \( g ' (x) = \cos x \) entonces
\( f ' (x) = 1 \) y \( g(x) = \sin x \)
De la fórmula de integración por partes anterior,
\( \displaystyle \int \; x \cos x \; dx = x \sin x - \int 1 \sin x dx \)
\( = x \sin x + \cos x + c \)

Más Preguntas con Soluciones

Utiliza la tabla de fórmulas de integrales y las reglas anteriores para evaluar las siguientes integrales. [Nota que puede ser necesario utilizar más de una regla anterior para una integral].
1. \( \displaystyle \int (1 / 2) \ln \; (x) dx \)
2. \( \displaystyle \int (\sin (x) + x^5 ) \; dx \)
3. \( \displaystyle \int (\sinh (x) - 3) \; dx \)
4. \( \displaystyle \int - x \sin (x) \; dx \)
5. \( \displaystyle \int \sin^{10}(x) \; \cos(x) dx \)

Soluciones a las Preguntas Anteriores

Más Referencias y Enlaces