Si \( f \) es una función continua en el intervalo \( [ a , b ] \) y diferenciable en \( (a , b ) \) , entonces existe al menos un número real \( c \) en el intervalo (a , b) tal que
\( f'(c) = \dfrac{{f(b) - f(a)}}{{b - a}} \).
El teorema del valor medio expresa la relación entre la pendiente de la tangente a la curva en \( x = c \) y la pendiente de la secante a la curva a través de los puntos (a , f(a)) y (b , f(b)).
Problema 1
Encuentra un valor de \( c \) tal que se cumpla la conclusión del teorema del valor medio para
\[ f(x) = -2x^3 + 6x - 2 \]
en el intervalo [-2 , 2]
Solución al Problema 1
\( f(x) \) es una función polinómica y es continua y diferenciable para todos los números reales. Evaluemos \( f(x) \) en \( x = -2 \) y \( x = 2 \)
\( f(-2) = -2(-2)^3 + 6(-2) - 2 = 2 \)
\( f(2) = -2(2)^3 + 6(2) - 2 = - 6 \)
Evaluamos \( \dfrac{{f(b) - f(a)}}{{b - a}} \)
\( \dfrac{{f(b) - f(a)}}{{b - a}} = \dfrac{{-6 - 2}}{{2 - (-2)}} = -2 \)
Ahora encontremos \( f'(x) \).
\( f'(x) = - 6x^2 + 6 \)
Construimos una ecuación basada en \( f'(c) = \dfrac{{f(b) - f(a)}}{{b - a}} \)
\( -6c^2 + 6 = -2 \)
Resolvemos para \( c \) para obtener 2 soluciones
\( c = 2 \sqrt{\dfrac{1}{3}} \) y \( c = - 2 \sqrt{\dfrac{1}{3}} \)
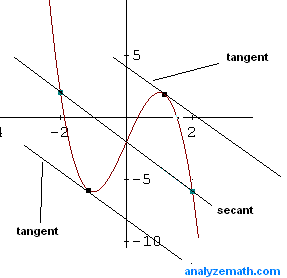
A continuación se muestra el gráfico de \( f \), una secante y las dos tangentes correspondientes a las dos soluciones encontradas. La secante y las dos tangentes son paralelas ya que sus pendientes son iguales según el teorema del valor medio.
Problema 2
Usa el teorema del valor medio para demostrar que para cualquier par de números reales \( a \) y \( b \),
\[ | \cos a - \cos b| ≤ | a - b| \]
Solución al Problema 2
La función \( \cos x \) es continua y diferenciable para todos los números reales. Usamos el teorema del valor medio, utilizando 2 números reales \( a \) y \( b \) para escribir
\[ (\cos x)' = \dfrac{{\cos a - \cos b}}{{a - b}} \]
Tomamos el valor absoluto de ambos lados
\[ | (\cos x)' | = \left| \dfrac{{\cos a - \cos b}}{{a - b}} \right| \]
\( (\cos x)' = - \sin x \), y por lo tanto \( | (\cos x)' | ≤ 1 \)
Lo cual nos da
\[ \left| \dfrac{{\cos a - \cos b}}{{a - b}} \right| ≤ 1 \]
A partir de las propiedades del valor absoluto, tenemos
\[ \left| \dfrac{\cos a - \cos b}{a-b} \right| = \dfrac{|\cos a - \cos b|} { |a - b|} \]
Cuando se combina con lo anterior, obtenemos
\[ \dfrac {| \cos a - \cos b |}{| a - b |} ≤ 1 \]
Multiplicamos ambos lados por | a - b | para obtener
\[ |\cos a - \cos b | ≤ | a - b | \]
