Problemas de optimización para Cálculo 1

Se presentan problemas de optimización para cálculo 1 con soluciones detalladas. Puede ser muy útil revisar primero cómo determinar el mínimo absoluto y máximo absoluto de una función utilizando conceptos de cálculo como la derivada de una función.

Pasos para resolver problemas de optimización

Problemas

Problema 1
Encuentra dos números positivos tal que su producto sea igual a 10 y su suma sea mínima. Verifica tu respuesta gráficamente.

Solución del Problema 1
Sea \( x \) el primer número y \( y \) el segundo número, tal que \( x \gt 0 \) y \( y \gt 0 \) y \( S \) la suma de los dos números.
Suma: \( S = x + y \), cantidad a optimizar tiene dos variables
Producto: \( x \cdot y = 10 \), relación dada entre las dos variables
Resuelve lo anterior para \( y \)
\( y = \dfrac{10}{x} \)
Sustituye \( y \) por \( \dfrac{10}{x} \) en la suma
\( S(x) = x + \dfrac{10}{x} = \dfrac{x^2 + 10}{x} \) con dominio \( x \gt 0 \), la cantidad a optimizar contiene solo una variable
Encuentra la primera derivada de \( S \)
\( S'(x) = \dfrac{x^2-10}{x^2} \)
Ceros de la derivada
\( x = \sqrt{10} \) y \( x = -\sqrt{10} \), Ceros de la primera derivada son puntos críticos
Selecciona \( x \) positivo: \( x = \sqrt{10} \) es un punto crítico de \( S \), Selecciona puntos críticos en el dominio
El dominio de \( S \) no tiene puntos finales y \( S \) por lo tanto puede tener un mínimo en el punto crítico.
Calcula la segunda derivada de \( S \)
\( S''(x) = \dfrac{20}{x^3} \), El signo de la segunda derivada da la concavidad que a su vez indica si tenemos un mínimo o un máximo
Como \( x \gt 0 \), \( S''(\sqrt{10}) \) es positivo (concavo hacia arriba) lo que confirma que \( S \) tiene un mínimo en \( x = \sqrt{10} \)
Los dos números positivos \( x \) y \( y \) cuyo producto es igual a 10 y su suma es mínima son:
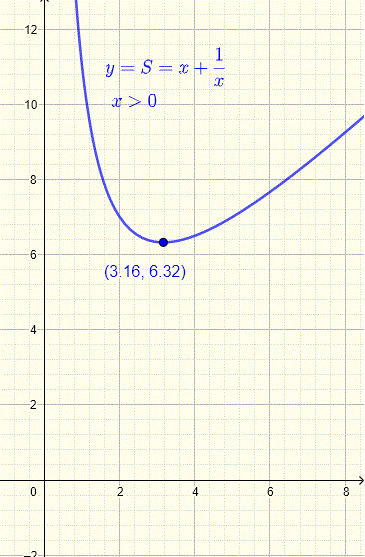
\( x = \sqrt{10} \approx 3.16 \) y \( y = \dfrac{10}{\sqrt{10}} = \sqrt{10} \approx 3.16 \)
El gráfico a continuación es el de la cantidad a optimizar \( S = x + \dfrac{10}{x} \) que tiene un valor mínimo en \( x \approx 3.16 \)

Problema 2
Encuentra dos números positivos tales que la suma de seis veces el primero y dos veces el segundo sea igual a 150 y su producto sea máximo.

Solución del Problema 2
Sea \( x \) el primer número y \( y \) el segundo número y \( P \) el producto de los dos números.
\( P = x \cdot y \)
\( 6x + 2y = 150 \), dada
Resuelve lo anterior para \( y \)
\( y = 75 - 3x \)
Sustituye \( y \) por \( 75 - 3x \) en \( P \)
\( P(x) = x \cdot (75 - 3x) = 75x - 3x^2 \)
Primera derivada de \( P \)
\( P'(x) = 75 - 6x \)
Cero de la derivada
\( x = \frac{75}{6} = \frac{25}{2} \)
Segunda derivada de \( P \)
\( P''(x) = -6 \), segunda derivada negativa, concavidad hacia abajo, lo que confirma que \( P \) tiene un máximo en \( x = \frac{25}{2} \)
\( y = 75 - 3x = 75 - 3 \cdot \frac{25}{2} = \frac{75}{2} \)

Problema 3
Supongamos que tienes que cercar dos campos rectangulares con las mismas dimensiones, con un lado en común, usando 180 metros de vallas. Encuentra las dimensiones de los rectángulos para que el área cercada total sea máxima.

Solución del Problema 3
Dibuja un diagrama tal que \( L \) sea la longitud y \( W \) el ancho de cada rectángulo y el ancho sea el lado común.

El área total de los dos rectángulos es: \( A = 2L \cdot W \)
La longitud total de las vallas es: \( 4L + 3W = 180 \)    (Ecuación 1)
Resuelve la ecuación anterior para \( W \)
\( W = 60 - \frac{4}{3} L \)
Sustituye \( W \) por \( 60 - \frac{4}{3} L \) en la fórmula del área \( A \)
\( A(L) = 2L(60 - \frac{4}{3} L) = - \frac{8}{3} L^2 + 120L \)
Hay varias formas de encontrar el dominio de \( A \). Usemos un método gráfico.
Graficamos la ecuación lineal \( 4L + 3W = 180 \) como se muestra a continuación y determinamos el rango de valores que toma \( L \).


Del gráfico, tenemos
El valor más pequeño de \( L \) es cero
El valor más grande de \( L \) es 45
Por lo tanto, el dominio de \( A \) está dado por el intervalo: \( L \in [ 0, 45] \)
Calcula la primera derivada de \( A \) con respecto a \( L \)
\( A'(L) = - \frac{16}{3}L + 120 \)
Encuentra los ceros de \( A' \)
\( - \frac{16}{3}L + 120 = 0 \)
Resuelve la ecuación anterior para \( L \)
\( L = 22.5 \)
Evalúa \( A \) en el punto crítico y los puntos finales.
\( A(22.5) = - \frac{8}{3}(22.5)^2 + 120(22.5) = 1350 \)
\( A(0) = 0 \)
\( A(45) = - \frac{8}{3}(45)^2 + 120(45) = 0 \)
\( A(L) \) tiene un máximo absoluto para \( L = 22.5 \) metros
y \( W = 60 - \frac{4}{3}(22.5) = 30 \) metros
Las dimensiones de cada rectángulo son: \( 22.5 \) por \( 30 \)

Problema 4
Un alambre de 100 cm se corta en dos piezas para hacer un cuadrado y un círculo. Encuentra la longitud de cada pieza de alambre para que la suma del área del cuadrado y del círculo sea mínima.

Solución del Problema 4
Sea \( x \) la longitud de la primera pieza para hacer un cuadrado y \( y \) la segunda pieza para hacer un círculo. \( x \) e \( y \) son el perímetro y la circunferencia del cuadrado y del círculo respectivamente.


\( x + y = 100\)    (Ecuación 1)
Sea \( s \) el lado del cuadrado. Dado que \( x \) es el perímetro del cuadrado, escribimos
\( x = 4 s \)
Por lo tanto, el lado \( s \) del cuadrado está dado por
\( s = \dfrac{x}{4} \)
Sea \( r \) el radio del círculo. Dado que \( y \) es la circunferencia del círculo, escribimos
\( y = 2 \pi r \)
Por lo tanto, el radio \( r \) del círculo está dado por
\( r = \dfrac{y}{2 \pi} \)
Sea \( A \) el área total encerrada por el cuadrado y el círculo
\( A = s^2 + \pi r^2 \)
Sustituye \( s \) y \( r \) por sus expresiones anteriores
\( A = \left (\dfrac{x}{4} \ \right)^2 + \pi \left( \dfrac{y}{2 \pi} \right)^2 \)
Simplifica
\( A = \dfrac{x^2}{16} + \dfrac{y^2}{4 \pi} \)
Resuelve la Ecuación 1 para \( y \)
\( y = 100 - x \)
Sustituye \( y \) por \( 100 - x \) en \( A \) arriba
\( A(x) = \dfrac{x^2}{16} + \dfrac{(100-x)^2}{4 \pi} \)
En teoría, \( x \) puede tomar valores desde cero hasta \( 100 \); por lo tanto, el dominio de \( A \) está dado por el intervalo: \( x \in [0,100] \)
Calcula la primera derivada de \( A \)
\( A'(x) = \dfrac{x}{8}-\dfrac{1}{2\pi }(100-x) \)
Encuentra los ceros de \( A' \)
\(\dfrac{x}{8}-\dfrac{1}{2\pi }(100-x) = 0 \)
Resuelve para \( x \)
\( x = \dfrac{400}{\pi +4} \approx 56\) metros
Evalúa \( A \) en los puntos críticos y los extremos
\( A(56) = \dfrac{56^2}{16} + \dfrac{(100-56)^2}{4 \pi} = 350 \)
\( A(0) = \dfrac{0^2}{16} + \dfrac{(100-0)^2}{4 \pi} = 795 \)
\( A(100) = \dfrac{100^2}{16} + \dfrac{(100-100)^2}{4 \pi} = 625 \)
El área total \( A \) es la más pequeña (mínima) en \( x = 56 \)
Ahora usamos la Ecuación 1 para encontrar \( y \)
\( y = 100 - x = 44\) metros

Problema 5
Se va a construir una caja con extremos cuadrados de lado \( x \) y una longitud \( L \) de modo que \( L + 4 x = 4 \) metros. Encuentra las dimensiones de la caja que proporcionen el mayor volumen.

Solución del Problema 5
El área de un extremo cuadrado de lado \( x \) es \( x^2 \)
El volumen \( V \) de la caja.
\( V = x^2 L \)
Resuelve la ecuación dada \( L + 4 x = 4 \) para \(L \)
\( L = 4 - 4 x \)
Sustituye \( L \) por \( 4 - 4 x \) en la expresión del volumen
\( V(x) = x^2 (4 - 4x) \)
El valor teórico más pequeño de \( x \) es cero. El valor más grande de \( x \) se obtiene estableciendo \( L = 0 \) en la ecuación dada \( L + 4 x = 4 \). Por lo tanto, el valor más grande de \( x \) es \( 1 \).
El dominio de \( V \) está dado por el intervalo cerrado: \( x \in [0,1] \)
Calcula la primera derivada de \( V \)
\( V'(x) = 8x-12x^2 \)
Encuentra los ceros de \( V' \)
\(8x - 12x^2 = 0 \)
Los puntos críticos son soluciones a la ecuación anterior: \( x = 0 \) y \( x = \dfrac{2}{3} \) y ambos están dentro del dominio
Evalúa \( V \) en los puntos críticos y los extremos.
\( V(0) = 0^2 (4 - 4(0)) = 0 \)
\( V(2/3) = (2/3)^2 (4 - 4(2/3)) = 16/27 \)
\( V(1) = (1)^2 (4 - 4(1)) = 0 \)
El volumen más grande se obtiene para \( x = 2/3 \)
Ahora usamos la ecuación dada para encontrar \( L \)
\( L = 4 - 4 x = 4/3 \) metros

Problema 6
El costo total, incluida la fabricación, el empaquetado y la distribución, de una calculadora electrónica es de $21. Si la máquina se vende a \( x \) dólares cada una, el número \( n \) de máquinas vendidas es \[ n = \dfrac{200}{x-21} + 10(50-x) \] ¿Qué precio de venta \( x \) maximizará la ganancia? (Pista: Ganancia = Ingresos totales para \( n \) máquinas - Costo total para \( n \) máquinas)

Solución del Problema 6
Sea \(R_t\) el ingreso total en la venta de \( n \) máquinas; se da por
\(R_t = n x\)
Sea \(C_t\) el costo total de fabricación, empaquetado y distribución de \( n \) máquinas; se da por
\(C_t = 21 n \)
La ganancia \( P \) para \( n \) máquinas se da por
\( P = R_T - C_T = n x - 21 n = n (x - 21) \)
Sustituye \( n \) por su expresión dada arriba y escribe
\( P = \left(\dfrac{200}{x-21} + 10(50-x) \right) (x - 21) \)
Simplifica
\( P(x) = 200 + 10(50-x)(x - 21) = -10x^2+710x-10300\)
El dominio de \( P \) es: \( x \in (0 , \infty) \) porque si el precio de venta \( x \) es menor o igual al costo de $21, no hay ganancia en absoluto y no hay límite superior para el precio de venta.
Calcula la primera derivada de \( P \)
\( P'(x) = -20x + 710 \)
Encuentra los ceros de \( V' \)
\(-20x + 710 = 0 \)
\( x = 35.5 \)
Como no hay puntos finales, usamos la segunda derivada para confirmar que la ganancia es máxima en \( x = 35.5 \).
Calcula la segunda derivada de \( V \)
\( P''(x) = -20 \)
La segunda derivada es negativa (cóncava hacia abajo) y confirma que la ganancia \( P \) es máxima para un precio de venta \( x = 35.5 \)

Problema 7
¿Cuáles son las dimensiones del rectángulo con el área más grande que se puede inscribir bajo el arco de la curva \( y = \dfrac{1}{x^2+1}\) y el eje x?

Solución del Problema 7
Sea \(x \) la mitad de la longitud del rectángulo. El vértice del rectángulo está en la curva y por lo tanto tiene una coordenada y igual a \( \dfrac{1}{x^2+1}\).


El ancho del rectángulo es igual a la coordenada y del vértice superior derecho como se muestra en el gráfico anterior. Por lo tanto, el área \( A \) del rectángulo es dada por
\( A(x) = 2 x \cdot \dfrac{1}{x^2+1} \)
El dominio de \( A \) está dado por el intervalo: \( x \in [0 , \infty) \)
Calcula la primera derivada de \( A \)
\( A ' (x) = \dfrac{2(x^2 + 1)-2x(2x)}{{\left(x^2+1\right)^2}} = \dfrac{2\left(1 -x^2\right)}{\left(x^2+1\right)^2} \)
Encuentra los ceros de \( A' \)
\(1-x^2 = 0 \)
Dos soluciones: \( x = 1 \) y \( x = - 1 \)
\( x \) es mayor o igual a cero, por lo que seleccionamos el punto crítico \( x = 1 \)
Calcula la segunda derivada de \( A \)
\( A''(x) = -\dfrac{4x(-x^2+3)}{(x^2+1)^3} \)
Calcula el valor de \( A'' \) para \( x = 1 \)
\( A''(1) = - 1 \)
\( A''(1) \) es negativo (cóncavo hacia abajo) y por lo tanto \( A \) es máximo en \( x = 1 \).
Las dimensiones del rectángulo con el área más grande son
Longitud = \( 2 x = 2(1) = 2 \)
Ancho = \( \dfrac{1}{1^2+1} = \dfrac{1}{2} \)

Problema 8
¿Cuáles son las dimensiones del rectángulo con el área más grande que se puede inscribir en el triángulo rectángulo de altura 4 y hipotenusa 5?

Solución del Problema 8
Es necesario un diagrama para este problema.


El área \( A \) del rectángulo está dada por
\( A = h \cdot w \)
Ahora necesitamos encontrar una relación entre \( h \) y \( w \).
Primero usamos el teorema de Pitágoras para encontrar la base BC del triángulo rectángulo
\( BC = \sqrt{5^2 - 4^2} = 3 \)
Los triángulos AEF y ABC son similares, por lo tanto, la igualdad de las razones
\( \dfrac{AE}{EF} = \dfrac{AB}{BC} \)
\( AE = 4 - h\) , \( EF = w \) , \( AB = 4 \) y \( BC = 3 \)
Sustituyendo
\( \dfrac{4-h}{w} = \dfrac{4}{3} \)
\( h = - \dfrac{4}{3} w + 4 \)
Sustituye \( h \) por la expresión anterior en el área \( A \)
\( A = (- \dfrac{4}{3} w + 4) w = - \dfrac{4}{3} w^2 + 4w \)
El dominio de \( A \) está dado por: \( w \in [0 , 3] \)
Calcula la primera derivada de \( A \)
\( A '(w) = - \dfrac{8}{3} w + 4 \)
Encuentra los ceros de \( A' \)
\(- \dfrac{8}{3} w + 4 = 0 \)
punto crítico, solución de la ecuación anterior: \( w = \dfrac{3}{2} \)
Evalúa \( A \) en el punto crítico y el extremo del dominio
\( A(3/2) = 3\)
\( A(0) = 0 \)
\( A(3) = 0 \)
El rectángulo tiene un área máxima para \( w = 3/2 \)
Las dimensiones del rectángulo con el área máxima son
\( w = x = \dfrac{3}{2} \)
\( h = - \dfrac{4}{3} w + 4 = - \dfrac{4}{3} \dfrac{3}{2} + 4 = 2\)

Problema 9
Demuestra analíticamente que la función \( f(x) = - 5 - 4 \cos(x) + \cos(2x) \; , \; \text{para} \; 0 \le x \le 2\pi \) nunca es positiva.

Solución del Problema 9
Una manera de responder esta pregunta es mostrar que el valor máximo de la función \( f \) no es positivo.
Calcula la primera derivada de \( f \)
\( f '(x) = 4 \sin(x) - 2 \sin(2x) \)
Usa la identidad \( \sin(2x) = 2 \sin(x) \cos(x) \) para reescribir la derivada en forma factorizada como
\( f '(x) = 4 \sin(x) - 2 \sin(2x) = 4 \sin(x) - 4 \sin(x) \cos(x) = 4 \sin(x) (1 - cos(x) ) \)
\( \sin(x) = 0 \) ; da tres soluciones dentro del dominio \( [0 , 2\pi] \)
\( x = 0 \) , \( x = \pi \) y \( x = 2 \pi \)
\( 1 - cos(x) = 0 \) lo cual es equivalente a \( cos(x) = 1 \)
tiene dos soluciones dentro del dominio \( [0 , 2\pi] \)
\( x = 0 \) y \( x = 2\pi \)
Ahora determinamos el valor máximo absoluto de \( f \) en todos los ceros de la primera derivada y los extremos
\( f(0) = - 5 - 4 \cos(0) + \cos(2(0)) = - 8 \)
\( f(2\pi) = - 5 - 4 \cos(2\pi) + \cos(2(2\pi)) = - 8 \)
\( f(\pi) = - 5 - 4 \cos(\pi) + \cos(2(\pi)) = 0\)
El valor máximo de \( f(x) \) es igual a cero y por lo tanto \( f(x) \) nunca es positivo.

Problema 10
Encuentra el radio \( r \) de la base de un cono y su altura \( h \) de modo que la altura lateral sea \( 5 \) cm y su volumen sea el más grande.

Solución del Problema 10



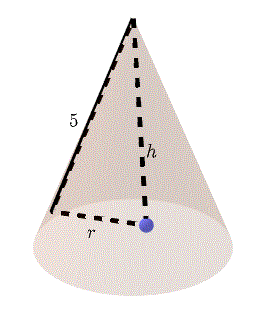
El volumen de un cono de radio \( r \) y altura \( h \) está dado por
\( V = \dfrac{1}{3} \pi r^2 h \)
Usando el teorema de Pitágoras, podemos escribir
\( h^2 + r^2 = 5^2 \)
Resuelve lo anterior para \( h \ )
\( h = \sqrt{25 - r^2} \)
Sustituye \( h \) en el volumen \( V \)
\(V(r) = \dfrac{1}{3} \pi r^2 \sqrt{25 - r^2} \)
El dominio de \( V \) está dado por: \( r \in [0,5] \)

Calcula la primera derivada de \( V \)
\( V '(r) = \dfrac{\pi}{3} (2r \sqrt{25 - r^2} + r^2 (\dfrac{1}{2}) (-2r) (25 - r^2)^{-1/2} ) = \dfrac{\pi}{3} \dfrac{(50r-3r^3)}{\sqrt{25-r^2}}\)
Encuentra los ceros de \( A' \)
\(50 r -3r^3 = 0 \)
Factoriza
\(r(50 - 3 r^2) = 0 \)
La ecuación anterior tiene tres soluciones: \( r = 0 \) , \( r = \sqrt{\dfrac{50}{3}} \approx 4.08 \) y \( r = - \sqrt{\dfrac{50}{3}} \approx - 4.08\).
\( r = - \sqrt{\dfrac{50}{3}} \) no está en el dominio y por lo tanto hay tres puntos críticos:
La función \( V \) tiene 3 puntos críticos: \( r = 0 \) , \( r = \sqrt{\dfrac{50}{3}} \) y \( r = 5 \)
\( r = 0 \) y \( r = \sqrt{\dfrac{50}{3}} \) hacen que \( V' = 0 \)
y \( r = 5 \) es un valor que hace que el denominador de \( V' \) sea igual a cero y por lo tanto la derivada \( V' \) es indefinida.

Evalúa \( V \) en los puntos críticos y los extremos.
\(V(\sqrt{\dfrac{50}{3}}) = \dfrac{1}{3} \pi (\sqrt{\dfrac{50}{3}})^2 \sqrt{25 - (\sqrt{\dfrac{50}{3}})^2} \approx 50.38\)

\(V(0) = \dfrac{1}{3} \pi 0^2 \sqrt{25 - 0^2} = 0 \)

\(V(5) = \dfrac{1}{3} \pi 5^2 \sqrt{25 - 5^2} = 0 \)

\( r = \sqrt{\dfrac{50}{3}} \approx 4.08 \) es el radio que da un volumen máximo.

Sustituye \( r \) por su valor numérico para obtener

\( h = \sqrt{25 - r^2} = \sqrt{25 - (\sqrt{\dfrac{50}{3}})^2} = \dfrac{5}{\sqrt{3}} \approx 2.88\)

Problema 11
Encuentra el punto en la línea dada por \( y = 4 - x \) que está más cercano al punto \( (6 , 3) \).

Solución del Problema 11
Primero necesitamos entender que por "más cercano" se entiende la distancia más pequeña.
Cualquier punto \( M \) en la línea \( y = 4 - x \) tiene coordenadas \( (x , 4 - x) \)


La distancia \( D \) entre el punto \( (6 , 3) \) y el punto \( M \) está dada por
\( D = \sqrt { (x - 6)^2 + (4 - x - 3)^2} = \sqrt { (x - 6)^2 + (1 - x)^2} \)
El dominio de \( D \) está dado por: \( x \in (-\infty,\infty) \)
Buscamos el punto \( M \) que está más cercano al punto \( (6 , 3) \) y por lo tanto estamos buscando la distancia \( D \) más pequeña entre estos dos puntos.

Calcula la primera derivada de la distancia \( D \)
\( D ' = \dfrac{1}{2} \dfrac{(4x-14)}{(2x^2-14x+37)^{1/2}} \)
Encuentra los ceros de \( D' \)
\(4x-14 = 0 \)
La solución de la ecuación anterior es \( x = \dfrac{7}{2}\) que es un punto crítico de \(D\)
No necesitamos encontrar la segunda derivada porque el signo de la primera derivada es fácil de obtener. El denominador es una raíz cuadrada y por lo tanto positivo. Por lo tanto, el signo de la primera derivada es el mismo que el signo del numerador \( 4x-14 \).
Para \( x < 14/4 \) , \( D' \) es negativa y para \( x > 14/4 \) , \( D' \) es positiva y por lo tanto la distancia \( D \) tiene un mínimo en \( x = 14/4 = 7/2\)
La coordenada y está dada por
\( y = 4 - x = 4 - 14/4 = 1/2 \)
el punto en la línea \( y = 4 - x \) que está más cercano al punto \( (6 , 3) \) tiene las coordenadas \( (7/2 , 1/2) \)

Problema 12
Una compañía debe construir un oleoducto desde el punto A en el mar (en el océano) hasta el punto B a lo largo de la costa. El costo del oleoducto que se construirá a lo largo de la costa es \( k \) dólares por kilómetro y el costo del oleoducto en alta mar es \( 3 k \) dólares, donde \( k \) es constante. Encuentra las distancias del oleoducto en alta mar desde A hasta D y a lo largo de la costa desde D hasta B para que el costo total del oleoducto de A a B sea el más bajo.




Solución del Problema 12
Sea \( x \) la distancia desde D hasta B (a lo largo de la costa) e \( y \) la distancia desde A hasta D (en alta mar) que necesitamos encontrar.
Usa el teorema de Pitágoras en el triángulo ACB para encontrar la distancia desde C hasta B.
\( CB = \sqrt{50^2 - 30^2} = 40 \) km
La distancia desde C hasta D es igual a \( CB - x = 40 - x \)
Usa el teorema de Pitágoras en el triángulo ACD para escribir
\( y = \sqrt{30^2 + (40 - x)^2} \)
El costo total C del oleoducto está dado por
\( C_t(x) = k x + 3 k y = k x + 3 k \sqrt{30^2 + (40 - x)^2} \)
\( x \) puede tomar valores de 0 a 40. Por lo tanto, el dominio de \( C_t \) está dado por el intervalo: \( x \in [0,40] \)

Encuentra la derivada de \( C_t \)
\( C_t '(x) = k - 3 k (1/2)(2)(40 - x) (30^2 + (40 - x)^2)^{-1/2} = k \dfrac{(30^2 + (40 - x)^2)^{1/2}-3(40-x)}{(30^2 + (40 - x)^2)^{1/2}} \)
Encuentra los ceros de \( C_t ' \) , k es una constante no igual a cero.
\( (30^2 + (40 - x)^2)^{1/2}-3(40-x) = 0 \)
\( (30^2 + (40 - x)^2)^{1/2} = 3(40-x) \)
Eleva ambos lados al cuadrado
\( \left((30^2 + (40 - x)^2)^{1/2}\right)^2 = (3 (40-x))^2 \)
\( 30^2 + (40 - x)^2 = 9x^2-720x+14400 \)
\( -8x^2+640x-11900 = 0 \)
La ecuación cuadrática anterior tiene dos soluciones pero una de ellas es una solución extranjera. La única solución válida para la ecuación original \( C'_t(x) = 0 \) es
\( x = \dfrac{(80-15\sqrt{2})}{2} \approx 29.40 \)
que es un punto crítico dentro del dominio.

Evalúa \( C_t \) para los dos extremos y el punto crítico
\( C_t(0) = 150 k \)
\( C_t(40) = 130 k \)
\( C_t(29.40) = 124.85 k \)
Por lo tanto \( x = 29.40 \) km da el costo total más bajo.
\( y \) está dado por
\( y = \sqrt{30^2 + (40 - 29.40)^2} = 31.81 \) km

Problema 13
Demuestra que si \( x + y = K \), donde \( K \) es una constante, entonces \( x \cdot y \le \left(\dfrac{K}{2} \right)^2 \).
\( x , y \) y \( K \) son números reales.

Solución del Problema 13
Necesitamos demostrar que el máximo del producto \( x \cdot y \) es menor o igual a \( \left(\dfrac{K}{2} \right)^2 \)
Expresa \( y \) en términos de \( x \)
\( y = K - x \)
Sea
\( P(x) = x \cdot y = x(K-x) = - x^2 + x K\)
El dominio de \( P \) está dado por el intervalo: \( x \in (-\infty , \infty) \)
Primera derivada de \( P \), recuerda que \( K \) es una constante
\( P'(x) = -2x + K \)
Encuentra los ceros de \( P' \)
\( -2x + K = 0 \)
Resuelve para \( x \)
\( x = K/2 \)
Encuentra la segunda derivada
\( P''(x) = -2\)
La segunda derivada es negativa (cóncava hacia abajo), por lo tanto \( P \) tiene un máximo en \( x = K/2 \)
Encuentra \( y \)
\( y = K - x = K - K/2 = K/2 \)
El valor máximo de \( P \) está dado por
\( P(K/2) = x \cdot y = \dfrac{K}{2} \cdot \dfrac{K}{2} = \left(\dfrac{K}{2} \right)^2 \)
Por lo tanto \( P = x \cdot y \le \left(\dfrac{K}{2} \right)^2 \)

Más Referencias y Enlaces

1. Mínimo y Máximo Absoluto de una Función.
2. Preguntas, Respuestas y Soluciones de Cálculo.
3. Tutoriales y Problemas Gratuitos de Cálculo.