Funciones Continuas en Cálculo
Presentamos una introducción y la definición del concepto de funciones continuas en cálculo con ejemplos. También se discuten los teoremas de continuidad y su uso en el cálculo.
Introducción y Definición de Funciones Continuas
Comenzamos primero con gráficas de varias funciones continuas. Se dice que las funciones cuyas gráficas se muestran a continuación son continuas ya que estas gráficas no tienen "roturas", "saltos" o "agujeros".
Ahora presentamos ejemplos de funciones discontinuas. Estas gráficas tienen: roturas, saltos o puntos en los que no están definidas.
En las gráficas de abajo, la función no está definida en \( x = 2 \). La gráfica tiene un agujero en \( x = 2 \) y se dice que la función es discontinua.
En las gráficas de abajo, los límites de la función por la izquierda y por la derecha no son iguales y, por lo tanto, el límite en \( x = 3 \) no existe. Se dice que la función es discontinua.
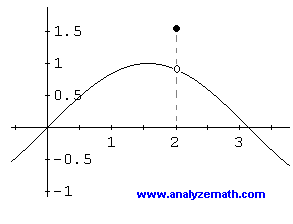
El límite de la función en \( x = 2 \) existe, pero no es igual al valor de la función en \( x = 2 \). Esta función también es discontinua.
El límite de la función en \( x = 3 \) no existe ya que a la izquierda y a la derecha de 3 la función aumenta o disminuye indefinidamente. Esta función también es discontinua.
Teniendo en cuenta toda la información recopilada de los ejemplos de funciones continuas y discontinuas mostradas anteriormente, definimos una función continua de la siguiente manera:
La función \( f \) es continua en un punto \( a \) si se cumplen las siguientes condiciones.
1. \(\lim_{x\to a} f(x)\) está definido
2. \(\lim_{x\to a} f(x)\) existe
3. \(\lim_{x\to a} f(x) = f(a)\)
Ejemplos con Soluciones
Ejemplo 1
Demuestra que la función \( f \) definida a continuación no es continua en \( x = - 2 \).
\( f(x) = \dfrac{1}{x + 2} \)
Solución al Ejemplo 1
\( f(-2) \) no está definida (división por 0 no permitida), por lo tanto, la función \( f \) es discontinua en \( x = - 2 \).
Ejemplo 2
Demuestra que la función \( f \) es continua para todos los valores de \( x \) en \( \mathbb{R} \).
\( f(x) = \dfrac{1}{x^4 + 6} \)
Solución al Ejemplo 2
La función \( f \) está definida para todos los valores de \( x \) en \( \mathbb{R} \). El límite de \( f \) en, digamos \( x = a \), viene dado por el cociente de dos límites: la constante 1 y el límite de \( x^4 + 6 \), que es una función polinómica y su límite es \( a^4 + 6 \). Por lo tanto,
\(\lim_{x\to a} f(x) = \dfrac{1}{a^4+6}\)
\( f(a) = \dfrac{1}{a^4 + 6} \). Por lo tanto,
\(\lim_{x\to a} f(x) = f(a)\)
Las tres condiciones de continuidad se satisfacen y, por consiguiente, \( f \) es continua para todos los valores de \( x \) en \( \mathbb{R} \).
Ejemplo 3
Demuestra que la función \( f \) es continua para todos los valores de \( x \) en \( \mathbb{R} \).
\( f(x) = | x - 5 | \)
Solución al Ejemplo 3
Primero escribamos \( f(x) \) de la siguiente manera. Por lo tanto,
\( f(x) = x - 5 \) si \( x > 5 \)
\( f(x) = -(x - 5) \) si \( x \lt 5 \)
\( f(x) = 0 \) si \( x = 5 \)
\( f(x) \) está dada por las funciones polinómicas \( x - 5 \) y \(-(x - 5) \) si \( x > 5 \) y \( x \lt 5 \) respectivamente, y por lo tanto \( f(x) \) es continua para estos valores de \( x \).
\( x = 5 \) es el único valor de \( x \) a considerar. Ahora consideramos los límites de \( f \) cuando \( x \) se acerca a \( 5 \) desde la izquierda (\( x \lt 5 \)) donde \( f(x) = -(x - 5) \).
\(\lim_{x\to 5^{-}} f(x) = \lim_{x\to 5^{-}} - (x - 5) = 0\)
Ahora consideramos los límites de \( f \) cuando \( x \) se acerca a \( 5 \) desde la derecha (\( x > 5 \)) donde \( f(x) = (x - 5) \).
\(\lim_{x\to 5^{+}} f(x) = \lim_{x\to 5^{+}} (x - 5) = 0\)
Dado que los dos límites son iguales, el límite \( \lim_{x\to 5} f(x) \) existe y es igual a 0. Por lo tanto, \( \lim_{x\to 5} f(x) = 0 = f(5) \) y la función \( f \) es continua en \( x = 5 \). Teniendo en cuenta lo dicho anteriormente para \( x > 5 \) y \( x \lt 5 \), \( f \) es continua para todos los valores de \( x \) en \( \mathbb{R} \).
Más referencias y enlaces
Tutoriales y Problemas de Cálculo