Un punto crítico de una función multivariable es un punto donde las derivadas parciales de primer orden de esta función son iguales a cero. Se presentan ejemplos con soluciones detalladas sobre cómo encontrar los puntos críticos de una función con dos variables.
Explora más problemas de optimización con funciones de dos variables en este sitio web.
En lo que sigue, \( C \) representa la constante de integración cuando corresponda.
Ejemplos con soluciones detalladas
Haz clic en cada ejemplo para ver su solución detallada paso a paso.
Ejemplo 1
Halla el o los puntos críticos de la función \( f \) definida por:
\[ f(x, y) = x^2 + y^2 \]Mostrar solución al ejemplo 1
Primero hallamos las derivadas parciales de primer orden:
\[ f_x(x, y) = 2x \] \[ f_y(x, y) = 2y \]Ahora resolvemos simultáneamente las siguientes ecuaciones \( f_x(x, y) = 0 \) y \( f_y(x, y) = 0 \):
\[ 2x = 0 \implies x = 0 \] \[ 2y = 0 \implies y = 0 \]La solución al sistema de ecuaciones anterior es el par ordenado \( (0, 0) \).
A continuación se muestra la gráfica de \( f(x, y) = x^2 + y^2 \), que muestra que en el punto crítico \( (0, 0) \), \( f \) tiene un valor mínimo.
Ejemplo 2
Halla el o los puntos críticos de la función \( f \) definida por:
\[ f(x, y) = x^2 - y^2 \]Mostrar solución al ejemplo 2
Halla las derivadas parciales de primer orden de la función \( f \):
\[ f_x(x, y) = 2x \] \[ f_y(x, y) = -2y \]Resuelve simultáneamente las ecuaciones \( f_x(x, y) = 0 \) y \( f_y(x, y) = 0 \):
\[ 2x = 0 \implies x = 0 \] \[ -2y = 0 \implies y = 0 \]La solución es el par ordenado \( (0, 0) \).
La gráfica de \( f(x, y) = x^2 - y^2 \) se muestra a continuación. La superficie se curva hacia abajo en la dirección de \( y \) y hacia arriba en la dirección de \( x \). \( f \) es estacionaria en \( (0, 0) \), pero no hay ningún extremo (máximo o mínimo). \( (0, 0) \) se denomina punto de silla porque la superficie cerca de \( (0, 0) \) se parece a una silla de montar.
Ejemplo 3
Halla el o los puntos críticos de la función \( f \) definida por:
\[ f(x, y) = -x^2 - y^2 \]Mostrar solución al ejemplo 3
Primero hallamos las derivadas parciales de primer orden:
\[ f_x(x, y) = -2x \] \[ f_y(x, y) = -2y \]Ahora resolvemos simultáneamente \( f_x(x, y) = 0 \) y \( f_y(x, y) = 0 \):
\[ -2x = 0 \implies x = 0 \] \[ -2y = 0 \implies y = 0 \]La solución es el par ordenado \( (0, 0) \).
La gráfica de \( f(x, y) = -x^2 - y^2 \) se muestra a continuación, ilustrando un máximo relativo.
Ejemplo 4
Halla el o los puntos críticos de la función \( f \) definida por:
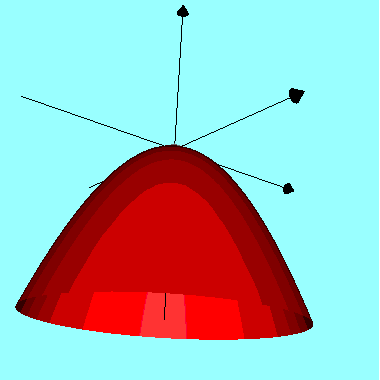
\[ f(x, y) = x^3 + 3x^2 - 9x + y^3 - 12y \]Mostrar solución al ejemplo 4
Las derivadas parciales de primer orden están dadas por:
\[ f_x(x, y) = 3x^2 + 6x - 9 \] \[ f_y(x, y) = 3y^2 - 12 \]Ahora resolvemos simultáneamente las ecuaciones \( f_x(x, y) = 0 \) y \( f_y(x, y) = 0 \):
\[ 3x^2 + 6x - 9 = 0 \implies 3(x + 3)(x - 1) = 0 \implies x = -3 \text{ o } x = 1 \] \[ 3y^2 - 12 = 0 \implies 3(y^2 - 4) = 0 \implies y = -2 \text{ o } y = 2 \]Combinando todas las combinaciones posibles de \( x \) y \( y \), los puntos críticos son:
\[ (1, 2), \; (1, -2), \; (-3, 2), \; (-3, -2) \]Ejercicios
Halla, si existen, los puntos críticos para las funciones siguientes. Haz clic en cada ejercicio para comprobar tus respuestas.
Ejercicio 1
\( f(x, y) = 3xy - x^3 - y^3 \)
Mostrar respuesta
Ejercicio 2
\( f(x, y) = e^{-x^2 - y^2 + 2x - 2y - 2} \)
Mostrar respuesta
Ejercicio 3
\( f(x, y) = \dfrac{1}{2}x^2 + y^3 - 3xy - 4x + 2 \)
Mostrar respuesta
Ejercicio 4
\( f(x, y) = x^3 + y^3 + 2x + 6y \)