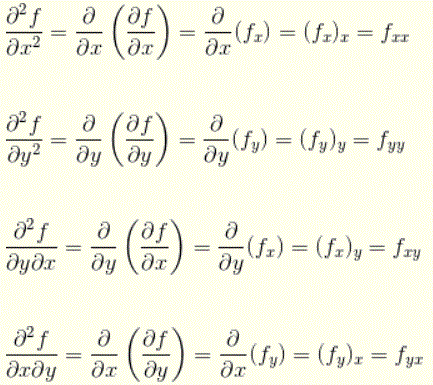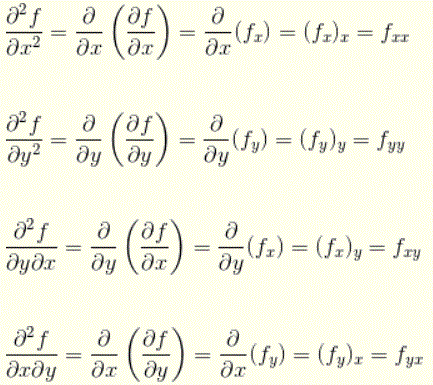Segundas Derivadas Parciales en Cálculo
Se presentan ejemplos con soluciones detalladas sobre cómo calcular segundas derivadas parciales parciales.
Definiciones y Notaciones de las Segundas Derivadas Parciales
Para una función de dos variables \( f(x , y) \), podemos definir 4 segundas derivadas parciales junto con sus notaciones.
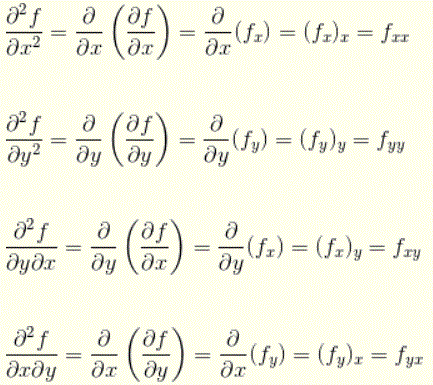
Ejemplos con Soluciones Detalladas sobre Segundas Derivadas Parciales
Ejemplo 1
Encuentra \( f_{xx} \), \( f_{yy} \) dado que \( f(x , y) = \sin(x y) \).
Solución
\( f_{xx} \) se puede calcular de la siguiente manera
\[
f_{xx} = \dfrac{\partial^2 f}{\partial x^2} = \dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial x}\right) = \dfrac{\partial}{\partial x}\left(\dfrac{\partial}{\partial x}\sin (x y)\right) = \dfrac{\partial}{\partial x}(y \cos (x y)) = - y^2 \sin (x y)
\]
\( f_{yy} \) se puede calcular de la siguiente manera
\[
f_{yy} = \dfrac{\partial^2 f}{\partial y^2} = \dfrac{\partial}{\partial y}\left(\dfrac{\partial f}{\partial y}\right) = \dfrac{\partial}{\partial y}\left(\dfrac{\partial}{\partial y}\sin (x y)\right) = \dfrac{\partial}{\partial y}(x \cos (x y)) = - x^2 \sin (x y)
\]
Ejemplo 2
Encuentra \( f_{xx} \), \( f_{yy} \), \( f_{xy} \), \( f_{yx} \) dado que \( f(x , y) = x^3 + 2 x y \).
Solución
\( f_{xx} \) se calcula de la siguiente manera
\[
f_{xx} = \dfrac{\partial^2 f}{\partial x^2} = \dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial x}\right) = \dfrac{\partial}{\partial x}\left(\dfrac{\partial}{\partial x}(x^3 + 2 x y)\right) = \dfrac{\partial}{\partial x}(3 x^2 + 2 y) = 6x
\]
\( f_{yy} \) se calcula de la siguiente manera
\[
f_{yy} = \dfrac{\partial^2 f}{\partial y^2} = \dfrac{\partial}{\partial y}\left(\dfrac{\partial f}{\partial y}\right) = \dfrac{\partial}{\partial y}\left(\dfrac{\partial}{\partial y}(x^3 + 2 x y)\right) = \dfrac{\partial}{\partial y}(2x) = 0
\]
\( f_{xy} \) se calcula de la siguiente manera
\[
f_{xy} = \dfrac{\partial^2 f}{\partial y\partial x} = \dfrac{\partial}{\partial y}\left(\dfrac{\partial f}{\partial x}\right) = \dfrac{\partial}{\partial y}\left(\dfrac{\partial}{\partial x}(x^3 + 2 x y)\right) = \dfrac{\partial}{\partial y}(3 x^2 + 2 y) = 2
\]
\( f_{yx} \) se calcula de la siguiente manera
\[
f_{yx} = \dfrac{\partial^2 f}{\partial x\partial y} = \dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial y}\right) = \dfrac{\partial}{\partial x}\left(\dfrac{\partial}{\partial y}(x^3 + 2 x y)\right) = \dfrac{\partial}{\partial x}(2x) = 2
\]
Ejemplo 3
Encuentra \( f_{xx} \), \( f_{yy} \), \( f_{xy} \), \( f_{yx} \) dado que \( f(x , y) = x^3y^4 + x^2 y \).
Solución
\( f_{xx} \) se calcula de la siguiente manera
\[
f_{xx} = \dfrac{\partial^2 f}{\partial x^2} = \dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial x}\right) = \dfrac{\partial}{\partial x}\left(\dfrac{\partial}{\partial x}(x^3y^4 + x^2 y)\right) = \dfrac{\partial}{\partial x}(3 x^2y^4 + 2 x y) = 6xy^4 + 2 y
\]
\( f_{yy} \) se calcula de la siguiente manera
\[
f_{yy} = \dfrac{\partial^2 f}{\partial y^2} = \dfrac{\partial}{\partial y}\left(\dfrac{\partial f}{\partial y}\right) = \dfrac{\partial}{\partial y}\left(\dfrac{\partial}{\partial y}(x^3y^4 + x^2 y)\right) = \dfrac{\partial}{\partial y}(4x^3y^3 + x^2) = 12x^3y^2
\]
\( f_{xy} \) se calcula de la siguiente manera
\[
f_{xy} = \dfrac{\partial^2 f}{\partial y\partial x} = \dfrac{\partial}{\partial y}\left(\dfrac{\partial f}{\partial x}\right) = \dfrac{\partial}{\partial y}\left(\dfrac{\partial}{\partial x}(x^3y^4 + x^2 y)\right) = \dfrac{\partial}{\partial y}(3x^2y^4 + 2 x y) = 12x^2y^3 + 2x
\]
\( f_{yx} \) se calcula de la siguiente manera
\[
f_{yx} = \dfrac{\partial^2 f}{\partial x\partial y} = \dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial y}\right) = \dfrac{\partial}{\partial x}\left(\dfrac{\partial}{\partial y}(x^3y^4 + x^2 y)\right) = \dfrac{\partial}{\partial x}(4x^3y^3 + x^2) = 12x^2y^3 + 2x
\]
Más Referencias y Enlaces a Derivadas Parciales y Funciones Multivariables
Funciones Multivariables